Преобразование Хартли

Лекция 19. Преобразование Хартли

Преобразование Хартли является аналогом преобразования Фурье, отображая вещественный сигнал в вещественный. Положим . Тогда . Найдем формулу обращения. Для этого установим связь с преобразованием Фурье. По определению  - = . Найдем обратное преобразование. ++. По определению, функция  - четная, а  - нечетная. В силу этого, два последних слагаемых равны 0. Далее, пользуясь теми же соображениями, напишем, что 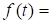+. Это означает, что, обратным к преобразованию Хартли является оно само.

Связь с преобразованием Фурье

Из определения вытекает формула, позволяющая найти преобразование Фурье, если известно преобразование Хартли.

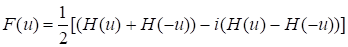
Обратно

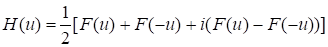
Дискретное преобразование Хартли

Покажем, что функции , когда  обладают свойством ортогональности. Действительно, положим  . Воспользуемся обозначением . В этих обозначениях . =. Нетрудно видеть, что матрица перехода от одного базиса к другому является унитарной. Отсюда вытекает ортогональность нового базиса.

Преобразование Хартли используется для вычисления спектра, который аналогичен спектру Фурье. Недостаток заключается в отсутствии простой зависимости преобразования от сдвига.

Преобразование Адамара.

Все предыдущие преобразования требовали значительных вычислений. Преобразование Адамара не требует вычислительных ресурсов. В основе лежит понятие матрицы Адамара. Это матрица, каждый элемент которой есть , а строки ортогональны. Особую роль играют матрицы  порядка . Они строятся согласно рекуррентному соотношению:. То что в результате получается матрица Адамара, проверяется непосредственно. . Преобразование вычисляется согласно формуле . Обратное находится очевидным образом.