Характеристики псевдослучайных последовательностей

Характеристики псевдослучайных последовательностей (ПСП)

Характеристиками ПСП являются функции автокорреляции (ФАК) и взаимной корреляции (ФВК), периодические и апериодические. ФАК и ФВК  вычисляются подсчетом разности числа совпадающих и не совпадающих разрядов сравниваемых ПСП при сдвигах одной из них.

Периодические ФАК и ФВК вычисляются при циклическом сдвиге ПСП.

Апериодические ФАК и ФВК вычисляются при обычном сдвиге ПСП (сравниваются части ПСП различной длины – от максимальной до минимальной).

 Смешанно-периодическая ФВК вычисляется при циклическом сдвиге одной кодовой комбинации относительно другой, составленной из разных ПСП.

В идеальном случае ФАК имеет один максимум, равный N - числу элементарных символов в ПСП, и не превышает ±1 при любом сдвиге ПСП. Идеальной ФАК, периодической и апериодической, обладают только коды Баркера. Они существуют при N= 3, 4, 5, 7, 11 и 13. Это коды 6, D, 1D, 72, 712, 1F35 (в 16-ричном представлении).

Периодические (а) и апериодические (б) автокорреляционные функции ПСП   1110010 идеальны. Периодическая функция взаимной корреляции последовательностей 1110010 и 1110100 не идеальна: ее максимальные выбросы равны 3 и -5 (в).

Способы формирования ПСП

Рекомендуемые материалы

Линейные ПСП формируются генератором, построенном на сдвиговом регистре с обратными связями, согласно алгоритму

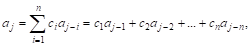
где а_i – состояния разрядов регистра. Коэффициенты с_i , принимающие значения 1 и 0, указывают номера разрядов, подключенных к логической схеме в цепи обратной связи. Суммирование выполняется по модулю 2. На регистр устанавливают начальный код и подают тактовые импульсы.

Чтобы использовать алгебраические методы при анализе характеристик ПСП, алгоритм ее формирования описывают характеристическим (порождающим) многочленом относительно фиктивной переменной «х»:

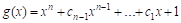
Нелинейные ПСП формируются с использованием нелинейной логической функции в цепи обратной связи, или в результате нелинейного преобразования линейной ПСП. Комбинированные и каскадные ПСП формируются из нескольких линейных ПСП. К настоящему времени разработаны достаточно большие ансамбли ПСП разных типов.

Свойства  m-последовательностей.

Максимальный период линейной псевдослучайной последовательности, полученной с использованием  n - разрядного регистра, равен 2ⁿ -1. Такие последовательности называют последовательностями максимальной длины, или m  - последовательностями. Необходимым (но не достаточным) условием получения m - последовательности является неприводимость порождающего многочлена – неразложимость на действительные множители.

Информация в лекции "Психологические и педагогические основы теории воспитания" поможет Вам.

Состояния разрядов регистра, генерирующего m- последовательность, составляют полный набор n-разрядных двоичных чисел, кроме нуля.

В одном периоде m - последовательности содержится равное (с точностью до 1) число знаков 1 и 0. Число пачек из «к» одинаковых знаков в 2 раза меньше числа пачек из «к-1» одинаковых знаков (к=2,..).

Сложение m - последовательности с ее копией, полученной циклическим сдвигом, дает другую циклически сдвинутую копию этой же ПСП.

Из m - последовательности можно получить все возможные m - последовательности той же длины путем децимации – выборки из исходной ПСП каждого к-го знака. В зависимости от значения «к» будут получаться либо новые ПСП, либо циклически сдвинутые копии исходной последовательности.

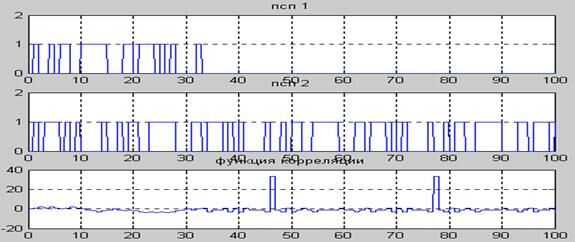
Периодические ФАК m-последовательностей идеальны.  На осциллограмме показана последовательность периода 31: исходная (один период) и сдвинутая (три периода), полученная на модели генератора ПСП. Вычисление функций корреляции начинается после завершения формирования ПСП, т.е. на втором и третьем периодах ПСП. ФАК имеет максимум величины 31, боковые лепестки ФАК равны 0 или -1.