Глава 2.

Устойчивость композитных конструкций

2.1. Основные понятия теории упругой устойчивости

Рассмотрим упругую механическую систему, подверженную действию консервативных внешних нагрузок.

Если внешние воздействия стационарны, то механическая система находится в состоянии равновесия, и ее полная потенциальная энергия имеет стационарное значение. Причем положение равновесия является устойчивым тогда и только тогда, когда стационарное значение полной энергии системы есть минимум (теорема Лагранжа)

         Э=U+A→min .                                            (2.1)

Необходимое условие экстремума функционала динамические и диссипативные выражается в виде вариационного уравнения Лагранжа

Рекомендуемые материалы

        

         δЭ=δ(U+A)=0                                            (2.2)

и используется при анализе стационарного (равновесного) состояния механической системы.

Поэтому для анализа характера стационарного поведения необходимо исследовать изменение полной энергии системы вблизи стационарного значения (рис.2.1)

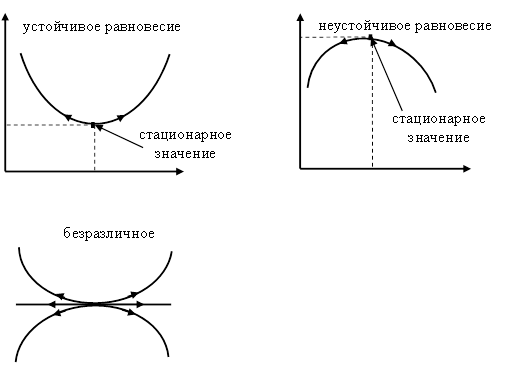
Рис. 2.1. Типы стационарного состояния механической системы

Обозначим ΔЭ приращение полной потенциальной энергии механической системы, вызванное вариацией поля  δU, то есть

         ΔЭ= Э[U] – Э[U+δU],                                  (2.3)

где U – поле перемещений, реализующее стационарное значение функционала Э.

Тогда для выполнения условия устойчивого равновесия достаточным условием будет

         ΔЭ ≤ 0 .                                               (2.4)

Таким образом, анализ устойчивости механической системы связан с задачами:

1. Определение условий возникновения неустойчивого равновесия (когда ΔЭ>0) (рис.2.2).

2. Поведение механической системы в области неустойчивого равновесия (характеризуется множественностью решений соответствующей краевой задачи, так называемое бифуркационное поведение и соответствующее этим условиям критические значения нагрузок и перемещений).

3. Закритическое поведение механической системы после прохождения зоны неустойчивости, переход к новому устойчивому положению равновесия системы (ΔЭ≤0).

Рис. 2.2. Диаграмма равновесных состояний

Здесь U – характерное перемещение, Р – характерная нагрузка.

2.2. Энергетические критерии устойчивости

2.2.1. Энергетический критерий бифуркационной потери устойчивости

Рассмотрим деформируемую консервативную упругую систему. На механическую систему действуют нагрузки, изменяющиеся пропорционально параметру Р. Полную потенциальную энергию системы определим как

                   Э = U + A .                                                 (2.5)

Согласно теореме Лагранжа устойчивое равновесие системы будет только в том случае, если

                   ΔЭ ≤ 0                                                       (2.6)

при любых малых отклонениях от состояния равновесия.

Рассмотрим первоначальное состояние системы. Пусть система не нагружена (Р=0), тогда любое малое отклонение системы от недеформированного состояния будет приводить к тому, что появится приращение упругой энергии ΔU, а так как внешнее воздействие Р=0, то ΔА=0 и  U[?????????????? , т.е. начальное состояние является состоянием устойчивого равновесия.

Так как имеется состояние устойчивого равновесия упругой системы (при Р=0), то в силу непрерывности функционала Э, существует некоторая окрестность 0≤Р<Р_кр , в которой выполняется условие устойчивого равновесия ΔЭ>0.

Критическое значение Р_кр параметра нагрузки – это нижняя граница диапазона внешних нагрузок, при которых возможно неустойчивое равновесие механической системы.

Рассмотрим  последовательность равновесных состояний механической системы, добавляя малые приращения к полю перемещений так, чтобы функционал Э сохранял стационарное значение, и будем исследовать его приращение ΔЭ.

Приращение полной энергии на каждом шаге можно представить в виде

                   ΔЭ = W + PV,                                            (2.7)

где W и V некоторые функционалы, не зависящие от Р. Критическое условие перехода к новому состоянию определяется равенством ΔЭ=0, тогда

                   .                                                 (2.8.)

Проварьируем полученное выражение

     .          (2.9)

Откуда следует условие

         δ(ΔЭ) = 0   - энергетический критерий устойчивости.       (2.10)

Полученное соотношение позволяет вычислять точки бифуркации начального состояния, причем критической будет точка, соответствующая наименьшему значению параметра нагрузки Р.

Если нагружение системы  определяется несколькими параметрами (Р₁ и Р₂, например), то говорят о границе, пересечение которой означает бифуркацию (рис.2.3).

Рис. 2.3. Область устойчивости

2.2.2. Энергетический критерий упругой устойчивости в форме Брайана

Бифуркационный критерий устойчивости имеет вид δ(ΔЭ)=0, следовательно, необходимо исследовать величину приращения потенциальной энергии ΔЭ вызванную вариацией полей перемещений в окрестности стационарного поля.

Считаем, что задача определения начального НДС решена (δЭ=0) и соответствующее поле перемещений {u₀}={u₀,v₀,w₀} найдено. Тогда возмущенное поле перемещений можно представить в виде

{u}={u₀}+a{u₁},                                       (2.11)

где a – малая величина, {u₁} – вариация функций перемещений.

Так как при потере устойчивости механической системы наблюдаются большие смещения точек, то для анализа деформированного состояния упругой системы при потере устойчивости необходимо использовать нелинейные геометрические соотношения

ε_x=+

………………………………………….                       (2.12)

γ_xy=

Подставляем (2.11) в (2.12)

 ε_x=

₌  (2.13)

.

Проделав подобную процедуру для оставшихся геометрических соотношений можно убедиться, что возмущенное поле деформаций в теле можно представить как

.                                        (2.14)

Для упрощения анализа задачи устойчивости примем ряд допущений (или гипотез):

1. Начальное состояние описывается уравнениями линейной теории упругости. Следовательно:

  .                                             (2.15)

2. Пренебрегаем изменением формы и размеров тела в первоначальном состоянии (пренебрегаем членами вида   и т.д. в выражении (2.14)). Тогда

 .                                              (2.16)

Компоненты вектора  определяется следующим образом

.                              (2.17)

Выражения аналогичны линейной части уравнений (2.12) для возмущенного поля перемещений u₁.

Подставим соотношение (2.13) в выражение для полной потенциальной энергии системы в новом, смежном с начальным состоянием. При этом полную потенциальную энергию представим в виде разложения по степеням малого параметра, ограничиваясь линейным и квадратным слагаемыми

         Э=Э₀+αЭ₁+α²Э₂,                                         (2.18)

где Э₀ – полная потенциальная энергия в стационарном состоянии.

Если рассматривать слагаемое α{u₁} как вариацию поля перемещений, то слагаемое αЭ₁ (линейное слагаемое разложения по α) по определению будет вариацией потенциальной энергии стационарного состояния αЭ₁=δЭ₀.

В свою очередь приращение потенциальной энергии при переходе из начального равновесного состояния в смежное бесконечно близкое состояние равно

        

         ΔЭ =Э - Э₀ = α² Э₂.                                         (2.19)

Если действующие на систему нагрузки являются консервативными, то их работа

        

;                                 (2.20)

где {q} – объемные силы, {p} – поверхностные силы, V – объем тела, S – поверхность, на которой действует нагрузки.

 и, следовательно, в величину Э₂ консервативные силы не входят, а входят только коэффициенты при α² в выражении для энергии упругого деформирования U.

Таким образом

,             (2.21)

где [С] – матрица жесткости упругого материала.

Учитывая условие устойчивости упругой системы примет вид

,                   (2.22)

где {σ₀}=[С]{ε₀} – поле начальных напряжений.

Энергетический критерий устойчивости вида (2.22) известен как условие устойчивости Брайана.

2.2.3. Энергетический критерий устойчивости в форме Тимошенко

Возмущенно поле перемещений зададим в виде

,                                       (2.23)

где α – малая величина. Деформации,  соответствующие возмущенному состоянию, определим, ограничившись квадратичными слагаемыми

         .                                         (2.24)

Если принять гипотезу о справедливости линейной задачи теории упругости для невозмущенного состояния и пренебречь влиянием изменения размеров и формы конструкции до потери устойчивости, то для векторов  и  будут справедливы геометрические соотношения Коши (аналогично подходу Брайана), а компоненты тензора деформаций  свяжем с полем перемещений  нелинейными геометрическими соотношениями.

Подсчитывая значение приращения энергии (с точностью до постоянного множителя α²), получим

.  (2 .25)

Используя условие взаимности работ можно второе слагаемое представить в виде

,                                                (2.26)

где  и, применяя формулу Остроградского-Гаусса, перейдем к интегралу по поверхности S. При этом на части контура S₁, где заданы граничные условия в напряжениях {p}={p₀} и, следовательно, {p₂}≡0. На оставшейся части контура S₂, соответствующей кинематическим граничным условиям, получим

        

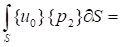
,                                  (2.27)

где  - кинематические граничные условия,  - реакции связей.

Окончательно критерий устойчивости принимает вид

,                                                  (2.28)

где             

- критерий в форме Тимошенко.

В отличие от критерия Брайана критерий устойчивости (2.28) не содержит начального поля напряжений {σ₀}, но требует определения поля дополнительных перемещений {u₂}, удовлетворяющего кинематическим граничным условиям и обеспечивающего условие стационарности δЭ₀=0.

2.3. Устойчивость стержней

Получим условие устойчивости прямолинейного упругого стержня на основе критерия  Брайана.

                            

Рис. 2.4. Схема нагружения стержня

Гипотезы:

1. Ось ненагруженного стержня идеально прямая.

2. Изменением размеров стержня до потери устойчивости пренебрегаем.

3. Изгиб стержня (смежная форма равновесия) описываем в рамках  линейной теории изгиба.

В  этом  случае  возмущенное  состояние  стержня  определяется функцией прогиба  w(x) .

       -  начальные  деформации, 

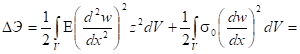
-     (2.29)

продольное  усилие  в  прямом  стержне. 

Окончательно имеем вариационную постановку задачи устойчивости  стержня   плюс граничные  условия.

Для получения постановки краевой задачи устойчивости в виде  дифференциального  уравнения  проварьируем  функционал  DЭ по w

.                                  (2.30)

Первое  слагаемое  интегрируем  дважды  по  частям, а  второе  один  раз

;             (2.31)

;               (2.32)

(вариация функции на неподвижном контуре равна 0);

                                   (2.33)

– основная  лемма  вариационного исчисления;

 на  интервале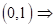

                                         (2.34)

– дифференциальное  уравнение  устойчивости  стержня.

2.4. Устойчивость  анизотропных  пластин

На основе энергетического подхода сформулируем критерий устойчивости пластины.

 

Рис. 2.5. Схема нагружения пластины

Основные  гипотезы:

1. До нагружения пластина плоская и ее не описывается соотношениями теории  упругости.

2. Изменением размеров пластины до потери устойчивости пренебрегаем.

3. Изгиб пластины (возмущенное состояние) описываем в рамках теории  изгиба пластин Тимошенко.

                                                                    

Перемещение  произвольной  точки  пластины  в  пространстве  xyz   определяется  при  изгибе  по  кинематической  модели  Тимошенко

                      

                                           (2.35)

где w – прогиб;  угол поворота нормали.

Кинематическая  модель справедлива как для стационарного, так и для  возмущенного  поля.

           

Подстановка  соотношения (2.35)  в  геометрические  соотношения  дает  для  возмущенных  деформаций: 

 и     (в  энергетическом  критерии  Брайана)

                                        (2.36)

В  учитываем только прогиб w.

Распишем выражение для приращения полной энергии для ортотропной  пластины (xy - оси ортотропии)

.

Неизвестные функции w, g₁, g₂ и не зависят от z, что позволяет провести  интегрирование по координате z с пределами где h - толщина  пластины.                   

,

 где  - изгибная  жесткость; - мембранная  жесткость;  - мембранные усилия в пластине в невозмущенном состоянии; - критерий устойчивости пластины.

Если  для  вариационного  уравнения  устойчивости  пластины поставить   систему  уравнений  Эйлера-Остроградского, то  можно  перейти  к  дифференциальной  постановке  задачи  устойчивости  пластины.

        

Так как  подынтегральная  функция  в  функционале  DЭ является  квадратичной, относительно неизвестных функций и их частных  производных, то уравнения Остроградского будут линейными  дифференциальными уравнениями  в частных  производных.  

2.5.  Устойчивость анизотропных оболочек

Задачу устойчивости тонких упругих оболочек рассмотрим на примере цилиндрической оболочки (рис.2.6).

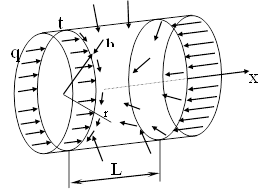
Рис. 2.6. Схема нагружения оболочки

Рассмотрим деформирование цилиндрической оболочки в рамках модели Тимошенко для оболочки малой кривизны (то есть пологой оболочки).

Компоненты деформации срединной поверхности (мембранной деформации) (рис.2.7)

  ,   ,    .                      (2.39)

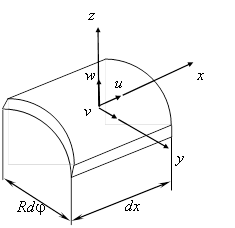
Рис. 2.7. Элемент оболочки

Углы поворота нормали:

 ,    .                                         (2.40)

Компоненты изгибной деформации (изменение кривизны срединной поверхности)

 ,  ,.                           (2.41)

Компоненты тензора линейных деформаций в произвольной точке оболочки определяют выражениями

                                         (2.42)

Тензор (2.) поле возможных деформаций первого рода  в выражении энергетического критерия устойчивости d(DЭ), для построения выражений для компонент тензора  учтем линейные слагаемые в тензоре мембранных деформаций:

;

;                                 (2.43)

.

Запишем выражение для приращения полной энергии цилиндрической оболочки:

.                             (2.44)

Подстановка (8.61) в первое слагаемое позволит произвести интегрирование по толщине оболочки, т. е. по координате z (от - h/2 до h/2, где h - толщина оболочки)

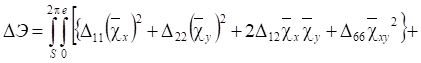
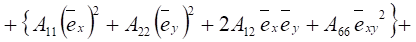
(2.45)

+.

В выражении DЭ   D_ij - компоненты тензора изгибных жесткостей            (D_ij = C_ij h³/12);  A_ij - тензор мембранных жесткостей (A_ij = C_ijh); T⁰_x , T⁰_y , T⁰_xy - тензор мембранных усилий для первоначального (невозмущенного) состояния  цилиндрической оболочки

                                                        

.                                              (2.46)

Для замкнутой цилиндрической оболочки на ее торцах должны быть заданы граничные условия:

v перемещение U или осевая елка T_x;

v перемещение v или угловое усилие S_xy;

v перемещение w или поперечное усилие Q_x;

v угол поворота нормали  g или  изгибающий момент M_x .

Если на оболочку действуют

· осевое усилие (сжимающее)           N N

· закручивающий момент      M      M

· и внешнее давление   p             

то мембранные усилия определяются следующим образом

;       

;                                      (2.47)

.

Получим систему дифференциальных уравнений устойчивости цилиндрической оболочки

 .    (2.48)     

Составим систему уравнений Остроградского-Эйлера:

                 (2.49)

Так, для осесимметричной формы потери устойчивости (u=vº0) при действии продольной нагрузки

.                                       (2.50)

При проведении практических расчетов устойчивости оболочечных конструкций обычно используют вариационную подстановку d(DЭ)=0 для получения разрешающих соотношений, например, в форме МКЭ.

2.6. Нелинейные задачи теории устойчивости

Линейная теория устойчивости, в рамках которой получен энергетический критерий бифуркационной устойчивости и линеаризованные уравнения устойчивости, не позволяет исследовать поведение механической системы после потери устойчивости.

 Причины:

 

1. Конечные перемещения (большие деформации).

2. Неупругое поведение материала (физическая нелинейность) при                                             наличии больших    деформаций.                                            

3. Динамические эффекты, сопровождающие переход из неустойчивого состояния равновесия в смежное устойчивое.

        

Кроме того, для элементов конструкций могут не выполняться и основные гипотезы теории устойчивости:

1. Первоначальное состояние системы может не описываться соотношениями линейной теории упругости (линейной теории          стержней, пластин и оболочек).

2. Первоначальная форма может иметь отклонения от идеальной       (стержень не прямой, пластина не плоская, кольцо не круглое).       

3. Действующие на систему нагрузки не являются «мертвыми», неизменяемыми по величине и направлению (например, нестационарное воздействие).

        

Все это приводит к усложнению задачи устойчивости, определяющие соотношение при этом получаются нелинейными.

                                              

Таким образом, при анализе закритического поведения конструкций, а также в некоторых случаях и при анализе условий потери устойчивости механических систем необходимо рассматривать нелинейные соотношения устойчивости (что безусловно является более сложной задачей).

         Закритическое поведение систем после потери устойчивости

Вариационные принципы механики:

1. Полная энергия стремится к минимуму (метод Лагранжа).

2. Дополнительная энергия стремится к минимуму (метод Кастильяно).

3. Мощность стремится к минимуму (метод Журдена).

Полная энергия представляет некоторый функционал, функция под интегралом не является квадратичной относительно неизвестной функции (поля перемещений, например перемещений).

                                                    (2.51)

Для функционалов такого вида несправедлив энергетический бифуркационный критерий устойчивости

d(DЭ) = 0.                                                      (2.52)

Однако из вариационного исчисления известно, что условие d(DЭ) = 0 является необходимым условием экстремума, а характер экстремума (минимум или максимум) определяется знаком второй вариации

d ²Э=d(dЭ) > 0 - min                                          (2.53)

и, следовательно,  предельное состояние для механической системы описывается уравнением              

,                                                       (2.54)

которое и является критерием устойчивости.

Легко убедиться, что бифуркационный критерий - частный случай приведенного соотношения. Разложение в ряд Тейлора приращения полной энергии дает

,                                          (2.55)    

 следовательно, DЭ = dЭ, если в разложение Тейлора ограничиться одним слагаемым, и тогда

 d²Э = d(dЭ) = d(DЭ).                                        (2.56)

Учитывая, что F в выражении для полной энергии содержит достаточно большое число неизвестных функций, то в выражении d²Э будет достаточно большое число слагаемых вида:

,                            (2.57)

причем, если неизвестных функций  n, то слагаемых - n².

Динамическая устойчивость

Если J - интеграл действия, то необходимое условие экстремума функционала (принцип Гамильтона)

,                                                  (2.58)

 а условие устойчивости движения

.                                                  (2.59)

Учет начальных несовершенств

Поле перемещений, как стационарное, так возмущенное, представляется в виде:

 

,                                             (2.60)

 где U - полное поле перемещений,

        u₀ - начальное поле перемещений,

        u - отклонение от первоначального поля перемещений.

        

Наличие некоторых функций {u₀} в предположении, что несовершенства (их форма) известны, дают дополнительные слагаемые в выражения для d²Э, что может повлиять на знак. При этом, изменение может происходить как в сторону увеличения, так и в сторону снижения критической нагрузки.

        

Кроме того, следует иметь в виду, что начальные прогибы несовершенства имеют статистическую природу, и задача оценки устойчивости конструкции в этом случае является вероятностной. 
                       

 

Рис. 2.  Геометрическая интерпретация решений задач устойчивости

 

где       P - обобщенная нагрузка;      

Бесплатная лекция: "12 Либерально-буржуазные реформы" также доступна.

       U - характерное перемещение;

       P_кр>P хлопка, при несовершенствах;

       P_кр=P хлопка, при силовом нагружении;

       1, 2, 3 - без учета несовершенств;

       4 - с несовершенствами.