Многослойные нейронные сети
§ 4.4 Многослойные нейронные сети.
4.4.1 Сети обратного распространения
Сети обратного распространения получили свое название из-за используемого алгоритма обучения, в котором ошибка распространяется от выходного слоя к входному, то есть в направлении противоположном направления сигнала. Нейронная сеть обратного направления состоит из нескольких слоев нейронов, причем каждый нейрон предыдущего слоя связан с каждым нейроном последующего слоя. Рассмотрим двухслойную нейронную сеть.
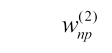
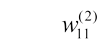
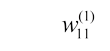
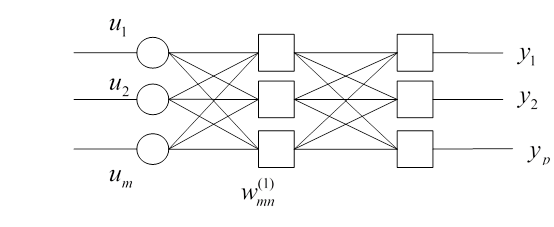
Матрицу весовых коэффициентов, соединяющие слои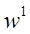 
, а 
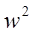— входы и первый слой. Пусть сеть обучается на выборке 
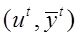задача — минимизация функции ошибки, которая находиться по методу наименьших квадратов.
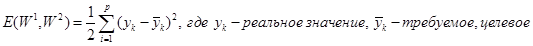
Обучение сети производиться известным оптимизационным методов градиентного спуска, то есть на каждой итерации изменение веса производиться по формулам:
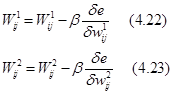
В качестве активационной функции обычно используется сигмаидальная функция. Производная:
Рекомендуемые материалы
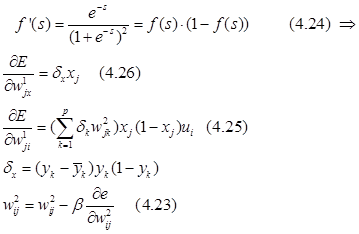
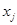– значение выхода j – го нейрона первого слоя.
Алгоритм обучения сети обратного распространения:
Алгоритм обратного распространения ошибки опишем для многослойной сети, имеющей входной слой l=0.
Несколько промежуточных (скрытых слоев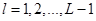 
) и выходной слой l = L.
l — нумерация слоев.
Будем считать, что каждый l слой содержит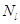 
нейронов. Таким образом, нейронная сеть имеет:
количество входов: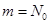 
выходов: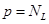 
.
Алгоритм 4.3
Исходные данные: обучающая выборка, то есть последовательность пар векторов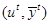 
для t=1,2,3..T, β — коэффициент скорости обучения, ε - параметр точности обучения, 
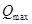-максимальное количество эпох.
Выход: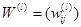 
размером 
.
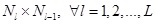Шаг 0: Инициализация весовых коэффициентов.
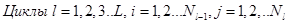
Синаптическим весам датчиком случайных чисел присвоить малые величины из интервала (-1,1). t=1.
Шаг 1: Подать на вход сети обучающий вектор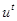 
.
Шаг 2:Прямой ход
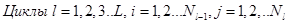
вычислить выходные сигналы j - ого нейрона в этом слое, следующим образом:
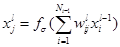, где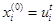 
- входные значения. И выходные сигналы сети: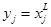 
Шаг 3: Обратный ход (коррекция весовых коэффициентов).
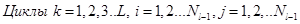
Вычислить
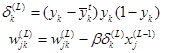
Здесь же в циклах:
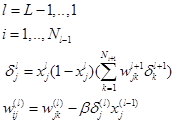
Шаг 4.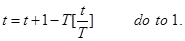 
4.4.3 Сети встречного распространения
Объединение разнотипных структур в один приводит к новым свойствам.
Нейронные сети встречного распространения - это гибридные сети, состоящие из входного слоя нейронов и слоев нейронов Кохенена и Гросберга. Эти сети по своим характеристикам существенно превосходят сети с однотипными нейронами (?).
Нейроны слоя Кохенна реализуют функцию порогового суммирования взвешенных входов, однако, в отличие от остальных слоев нейрон слоя Кохенна с максимальным значением взвешенной суммы на заданных входной вектор называется победителем, на его выходе формируется значение 1, а на выходах остальных - 0.
Слой Кохенна обучается без учителя на основе самоорганизации, т.е. самообучаемый слой. Число входов каждого нейрона этого слоя равно размерности вектора параметров объекта. А количество нейронов совпадает с требуемым числом классов на которые необходимое разбить объекты. Нейроны слоя Гросберга на выходе выдают величины весов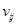 
, которые связывают с победителями нейронов Кохенана. В отличие от самообучающегося слоя Кохенена, слой Гросберга обучается с учителем.
Отличие от стандартной схемы обучения заключается в том, что подстройке подвергаются только те веса нейронов слоя Гросберга, которые соединены с ненулевым нейроном Кохенена.
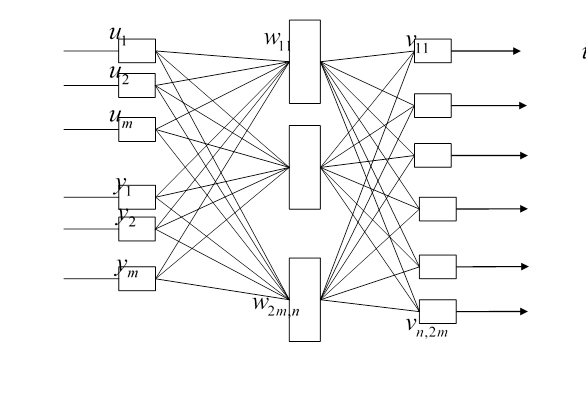
Отличие сети встречного распространения заключается так же в особенностях функционирования. В соответствии с приведенной на рисунке структурой на вход сети подаются нормализованные единичные векторы u, y. А на выходе формируются их нормализованные аппроксимации с волнами. При обучении входные вектора подаются как на вход, так и на выход.
Реализуется свойства ассоциативной памяти, заключающееся в том, что предъявление на вход только вектора y или u при отсутствии другого приводит к порождению на выходе как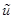 
, так и 
.
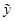4.4.4 Обучение сети встречного распространения.
Нормализованный вектор — вектор единичной длины.
Перед обучением сети предварительно проводят нормировку векторов обучающей выборки.
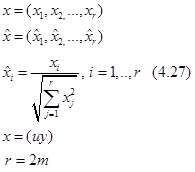
Если осуществить нормировку, а так же после каждого процесса осуществить нормировку каждого нейрона, то в качестве близости входных векторов и векторов нейронов можно рассматривать скалярное произведение между ними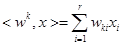 
.
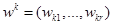— строка матрицы W.
Наименьшим будет расстояние до того нейрона, у которого будет скалярное произведение с которым у входного вектора максимально.
Алгоритм 4.4
Входные данные: обучающая выборка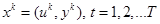 
:
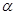- начальный коэффициент скорости обучения слоя К.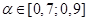 
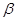- коэффициент скорости обучения слоя Г.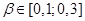 
Выход: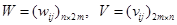 
Шаг 0: Весовым коэффициентам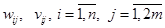 
присвоить малые случайные значений и произвести единичную нормировку матриц W,V по строкам. t=1.
Шаг 1: Для вектора x^t вычислить скалярные произведения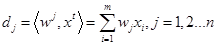 
Информация в лекции "5. Электронные информационные ресурсы" поможет Вам.
Шаг 2: Выбрать нейрон k 1<= k <= n с наибольшим скалярным произведением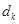 
.
Шаг 3: установить выход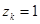 
, выходы всех остальным нейронов слоя Кохенена = 0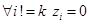 
Шаг 4: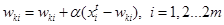 
Шаг5:Подать выходной вектор слоя Кохеннан на слой Гросберга и скорректировать веса по формуле: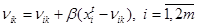 
Шаг 6: Уменьшить значения 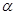и 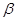, и изменить 
.
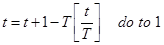