Синтез синхронных автоматов
Синтез синхронных автоматов
Основная модель синхронного автомата
Основная модель синхронного автомата (рис. 6) отличается от модели асинхронного потенциального автомата (см. рис. 3) лишь свойствами ЭП типа D, которые управляются тактовым сигналом Н. В синхронных ЭП тактовый сигнал Н оказывает на них импульсное воздействие только в момент изменения с 1 на 0 (или только с 0 на 1), а изменения информационных сигналов ЭП Dr=Q+r не воздействуют на ЭП, т.е. эта формула справедлива только при dH = 1, а при dH =0 сигнал Q+r = Qr.
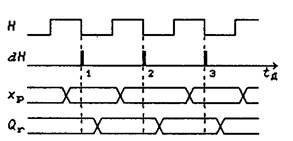 |
Понятно, что информационные сигналы Dr не должны изменяться при dH = 1, так как они при этом имеют неопределенное значение Ф, а значит, нарушается детерминированность переходов автомата. Из этого следует, что и входные сигналы автомата xp не должны изменяться при dH = 1.
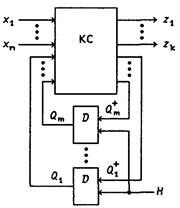 |
Рис.6. Рис.7.
Данные ограничения на изменения информационных сигналов описываются уравнениями
ÑDr×dH=0, Ñxp×dH=0.
На рис.7. показаны временные диаграммы, поясняющие работу синхронного автомата. Моменты изменения тактового сигнала с 1 на 0 задают дискретное время tд = 1, 2, 3,... . Только в данные дискретные моменты времени внутреннее состояние автомата может изменяться. Переходный процесс, вызванный в КС этим изменением в данный момент времени tд, должен окончиться к следующему дискретному моменту времени tд+ 1. Из этого следует, что максимальная частота тактового сигнала должна быть ограничена некоторой величиной. Понятно, что минимально допустимое значение периода тактового сигнала ТH (рис.7.) полностью определяется быстродействием ЭП и КС.
Заменив в переключательных функциях основной модели автомата непрерывное время на дискретное, получим функции переходов и выходов синхронного автомата:
Рекомендуемые материалы
Выполнение данных условий гарантирует детерминированность переходов автомата при ложных значениях функции переходов во время переходного процесса, так как они смогут появиться только при значении сигнала dH == 0, а значит не вызовут срабатывания ЭП. Следовательно, можно сказать, что синхронные ЭП (триггеры) обладают фильтрующими свойствами, так как все изменения информационных сигналов, происходящие на интервале времени, когда сигнал dH = 0, не пропускаются на их выход. Из этого следуют важные для синтеза синхронных автоматов вывод: КС могут синтезироваться несвободными от состязаний;
Исключение из рассмотрения в синхронных автоматах переходных процессов значительно упрощает методы их синтеза.
Этапы синтеза синхронных автоматов
Процесс проектирования синхронных цифровых устройств разделяется на несколько относительно независимых этапов.
1. Словесная постановка задачи проектирования или с помощью временных диаграмм самим исполнителем или заказчиком, который может и не владеть аппаратом формального синтеза.
2. Абстрактный синтез – предполагает переход от словесного описания автомата к одному из формальных способов его задания, т. е. к составлению графа переходов или таблиц переходов и выходов в символах абстрактных алфавитов. На этом же этапе выполняется кодирование, которое заключается в установке соответствия каждому абстрактному символу состояния входа vi, выхода wl и внутреннего состояния автомата sj наборов двоичных значений входных сигналов xp, выходных сигналов zq и внутренних состояний Qr.
3. Структурный синтез, предполагающий выбор элементной базы, включая типы ЭП (триггеров), составление и минимизация логических выражений для функций переходов Пr (функций возбуждения триггеров) и функций выходов Bq.
4. Схемная реализация, заключающаяся в построении функциональной и принципиальной схем автомата в выбранном элементном базисе, используя заданную серию интегральных схем (ИС).
5. Проверка правильности синтеза – получение в процессе работы автомата значений его внутренних состояний, выходных сигналов и сравнение их с заданными. Проверку удобно производить путем построения потактной таблицы или временных диаграмм.
Пример синтеза синхронного автомата
Требуется создать автомат по продаже газет стоимостью 3 рубля.
1 ЭТАП. Словесное описание работы автомата.
Автомат «ПРОДАВЕЦ ГАЗЕТ» получает монеты достоинством в один рубль и два рубля и выдает сообщения о достоинстве принятой монеты. Если полученная сумма монет равна трем рублям, то автомат выдает газету. Если сумма более трёх рублей, то автомат возвращает все деньги.
2 ЭТАП. Абстрактный синтез.
Определим множества состояний входов, выходов, внутренних состояний автомата и обозначим их соответствующими символами абстрактного алфавита.
Состояния входов автомата: v0- принята монета достоинством в 1 руб.;
v1 - принята монета достоинством в 2 руб.
Множество состояний входов автомата – V={ v0, v1}.
Состояния выходов автомата: w0 – выдача сообщения " Принята сумма 1 руб.";
w1 – выдача сообщения " Принята сумма 2 руб.";
w2 - выдача газеты;
w3 - возврат денег.
Множество состояний выходов автомата – W={ w0, w1, w2, w3}.
Внутренние состояния автомата: s0 - принята сумма 0 руб. (начальное состояние);
s1 - принята сумма 1 руб.;
s2 - принята сумма 2 руб.
Множество внутренних состояний автомата – S={ s0, s1, s2}.
Составляем таблицы переходов (табл.5), выходов (табл.6) и объединенную таблицу (табл.7).
| vi | sj | ||
| s0 | s1 | s2 | |
| v0 | s1,w0 | s2,w1 | s0,w2 |
| v1 | s2,w1 | s0,w2 | s0,w3 |
Таблица 5. Таблица 6. Таблица 7.
| vi | sj | ||
| s0 | s1 | s2 | |
| v0 | s1 | s2 | s0 |
| v1 | s2 | s0 | s0 |
| vi | sj | ||
| s0 | s1 | s2 | |
| v0 | w0 | w1 | w2 |
| v1 | w1 | w2 | w3 |
Этот же автомат можно задать в виде графа, вершины которого соответствуют состояниям автомата, а дуги - переходам (рис.2):
 |
Рис. 8.
Для уяснения работы автомата ПРОДАВЕЦ ГАЗЕТ приведём пример его реакции на заданную входную последовательность в виде табл.8:
Таблица 8.
| tД | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| vi(tД) | v0 | v0 | v1 | v1 | v0 | v1 | v1 | v0 | v0 | v0 | v1 | v0 |
| sj(tД) | s0 | s1 | s2 | s0 | s2 | s0 | s2 | s0 | s1 | s2 | s0 | s2 |
| wl(tД) | w0 | w1 | w3 | w1 | w2 | w1 | w3 | w0 | w1 | w2 | w1 | w2 |
Перед началом кодирования необходимо определить количество двоичных символов, которое требуется для отображения каждого множества состояний автомата в двоичных кодах. Если множество содержит N состояний, то требуемое количество двоичных символов (или разрядов) b вычисляется как ближайшее целое двоичного логарифма числа N:
b=]log2N[.
Исходя из сказанного, определяем количество двоичных разрядов, требуемое для кодирования:
множества, состоящего из двух состояний входов vi – n=]log22[=1;
множества, состоящего из четырех состояний выходов wl – k=]log24[=2;
множества, состоящего из трех состояний входов sj – m=]log23[=2.
Таким образом, создаваемый автомат имеет один вход, два выхода, и два ЭП.
Один из возможных вариантов кодирования состояний автомата представлен в табл.9-11.
Таблица 9. Таблица 10. Таблица11.
| vi | xp |
| X0 | |
| v0 | 0 |
| v1 | 1 |
| wl | zq | |
| z1 | z0 | |
| w0 | 0 | 0 |
| w1 | 0 | 1 |
| w2 | 1 | 0 |
| w3 | 1 | 1 |
| sj | Qr | |
| Q1 | Q0 | |
| s0 | 0 | 0 |
| s1 | 0 | 1 |
| s2 | 1 | 0 |
Таблица переходов-выходов автомата (см. табл.4) в кодированном виде представлена в табл.12.
Таблица 12.
| vi | sj | ||
| 00 | 01 | 10 | |
| 0 | 01,00 | 10,01 | 00,10 |
| 1 | 10,01 | 00,10 | 00,11 |
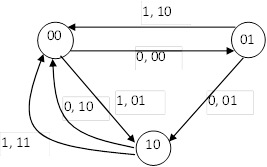 |
Кодированный граф переходов, в котором символы абстрактных алфавитов заменены соответствующим им двоичными кодами, изображен на рис 9.
Рис. 9.
3 ЭТАП. Структурный синтез автомата.
Любую логическую функцию можно представить в виде комбинации простейших логических функций. Набор простейших логических функций, с помощью которых можно записать любую логическую функцию называется логическим базисом. Такими базисами являются базис И, ИЛИ, НЕ (булев базис), базис И-НЕ, базис ИЛИ-НЕ и др.
Выберем булев базис.
На этом этапе выбираются виды ЭП (триггеры) из существующего множества типовых: R-S-, T-, D-, J-K-триггеры или их комбинации. Так как любой триггер является элементарным цифровым автоматом, то он описывается таблицей переходов. По таблицам переходов для всех типов триггеров строятся словари переходов, представленные в табл.13.
Таблица 13.
| Состояния триггера | R-S- триггер | J-K- триггер | D- триггер | T- триггер | |||
| Q | Q+ | R | S | J | K | D | T |
| 0 | 0 | * | 0 | 0 | * | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 | * | 1 | 1 |
| 1 | 0 | 1 | 0 | * | 1 | 0 | 1 |
| 1 | 1 | 0 | * | * | 0 | 1 | 0 |
В качестве ЭП синтезируемого автомата выберем J-K-триггер и D-триггер.
Составление и минимизацию логических выражений для функций переходов (функций возбуждения триггеров) и для функций выходов удобно выполнять с использованием расширенной кодированной таблицы переходов-выходов (табл.14).
Таблица 14.
| V | S | S+ | D | W | |||||
| x0 | Q1 | Q0 | Q+1 | Q+0 | J1 | K1 | D0 | z1 | z0 |
| 0 | 0 | 0 | 0 | 1 | 0 | * | 1 | 0 | 0 |
| 0 | 0 | 1 | 1 | 0 | 1 | * | 0 | 0 | 1 |
| 0 | 1 | 0 | 0 | 0 | * | 1 | 0 | 1 | 0 |
| 0 | 1 | 1 | * | * | * | * | * | * | * |
| 1 | 0 | 0 | 1 | 0 | 1 | * | 0 | 0 | 1 |
| 1 | 0 | 1 | 0 | 0 | 0 | * | 0 | 1 | 0 |
| 1 | 1 | 0 | 0 | 0 | * | 1 | 0 | 1 | 1 |
| 1 | 1 | 1 | * | * | * | * | * | * | * |
Ввиду того, что внутреннее состояние 11 не участвовало в кодировании состояний автомата, то реакция автомата, находящегося в состоянии 11, не определена. Автомат не может находиться в этом состоянии и для отличия обозначим значения функций для этого состояния символом Ф. Поэтому все полученные функции будут частичными.
Рассмотрим подробнее одну из строк табл.14, например, строку, соответствующую набору x0Q1Q0 = 101. Строка была получена из таблицы переходов-выходов (см. табл.12) следующим образом. Из состояния Q1Q0 =10 под воздействием входного сигнала х0 =0 автомат переходит в состояние Q+1Q+0 =00 и выдает выходной сигнал z1z0 = 10.
Продолжим заполнение строки, определяя значения функций возбуждения входов триггеров J1, K1, D01. При этом будем пользоваться словарями переходов триггеров (табл. 13). Значения функций возбуждения элементов памяти автомата должны быть такими, чтобы реализовался закон его функционирования. Первый элемент памяти автомата - D-триггер находился в нулевом состоянии и должен остаться в этом состоянии: Q0=0 ® Q+0=0. Это определяет значение функции D0=0. Второй элемент памяти должен переключится из единицы в нуль: Q1=1 ® Q+1 = 0. Поэтому J1 = *, а K1=1.
Аналогично заполняются все остальные строки табл.14 и определяются значения функций возбуждения триггеров на остальных наборах значений аргументов в соответствии с табл.13.
Минимизация логических выражений функций возбуждения триггеров Пr и выходов Bq выполняется с помощью карт Карно (или диаграмм Вейча). Карты Карно заполняются значениями функций возбуждения триггеров J1, K1, D0 и функций выходов z1, z0. Карты изображены на рис.9.
а) б)
| J1 | ||||
| Q1Q0 . x | ||||
| 00 | 01 | 11 | 10 | |
| 0 | 0 |
| Ф | * |
|
| 1 | 0 |
| * |
| K1 | ||||
| Q1Q0 . x | ||||
|
| 01 | 11 | 10 | |
| 0 | * | * | Ф | 1 |
| 1 | * | * | Ф | 1 |
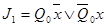 K1=1
K1=1
в) г)
| D0 | ||||
| Q1Q0 . x | ||||
|
| 01 | 11 | 10 | |
| 0 | 1 | 0 | Ф | 0 |
| 1 | 0 | 0 | Ф | 0 |
| Z1 | ||||
| Q1Q0 . x | ||||
| 00 | 01 |
| 10 | |
| 0 | 0 |
| Ф | 1 |
| 1 | 0 | 1 | Ф | 1 |
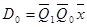
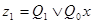
д)
| Z0 | ||||
| Q1Q0 . x | ||||
|
| 01 | 11 | 10 | |
| 0 | 0 | 1 | Ф | 0 |
|
| 1 | 0 | Ф |
|
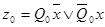
Рис.9.
4 ЭТАП. Схемная реализация.
Осуществляется построение функциональной и принципиальной схем в выбранном базисе и на заданной серии ИС.
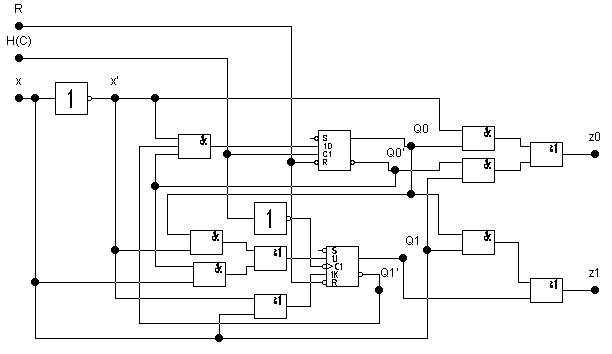
Функциональная схема приведена на рис 10.
Обратив внимание на то, что J1=z0, обе функции можно реализовать одной и той же схемой.
Если задана серия ИС, например серия 155, то пользуясь справочными данными, можно построить принципиальную схему автомата.
Ещё посмотрите лекцию "Тема 3. Спинной мозг" по этой теме.
Рис.10.
5 ЭТАП. Проверка правильности синтеза.
Проверку целесообразно выполнять путем моделирования работы созданной схемы автомата на ПК для заданной последовательности входных сигналов. Результатом моделирования являются временные диаграммы.
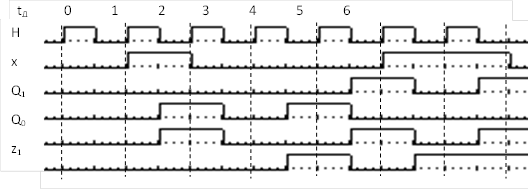 |
Пусть задана последовательность входных сигналов, под воздействием которой автомат выполняет последовательно все возможные переходы, заданные графом переходов: v0=0, v1=1, v0=0, v0=0, v0=0, v1=1, v1=1. Для этой последовательности при моделировании получены временные диаграммы, представленные на рис.11.
Рис.11.
На этом завершается процесс синтеза автомата.

 1
1 1
1 Ф
Ф 00
00 00
00 11
11 0
0 00
00 1
1 1
1

















