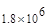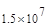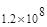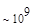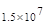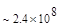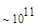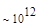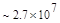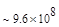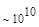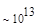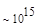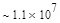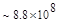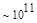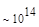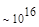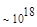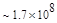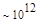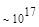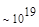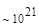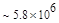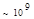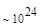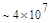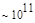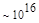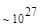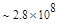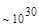Переход от систем данных
Лекция 12
4.8 Переход от систем данных к системам с поведением
Важный класс системных задач, часто называемый индуктивным моделированием систем. Все задачи этого класса характеризуются следующим общим описанием:
1. дана конкретная система х, определенного иерархического типа;
2. множество всех конкретных систем более высокого иерархического типа, совместимых с системой х (т. е. основанных на той же представляющей системе, с теми же методологическими отличиями) обозначим Y;
3. набор соответствующих требований Q относительно неких свойств систем из множества Y, причем одним из этих требований является требование, чтобы данная система х была аппроксимирована как можно точнее системой более высокого типа и требуется определить YQ — подмножество Y, такое, чтобы любая система из YQ удовлетворяла всем требованиям, определенным в наборе Q.
Набор требований Q может состоять из:
1) подмножества  множества Y, определенного АСНИ (как выбор по умолчанию);
множества Y, определенного АСНИ (как выбор по умолчанию);
Рекомендуемые материалы
2) требования, чтобы несогласованность между соответствующими переменными заданной системы данных и системы с поведением из YQ была как можно меньшей;
3) требование, чтобы степень неопределенности при порождении данных системой с поведением из подмножества YQ была как можно меньшей;
4) требованием, чтобы система из подмножества YQ была как можно более простой;
5) предпочтения требования 2 требованиям 3 и 4.
В этой общей формулировке требование 1 сводится к определению множества допустимых масок.
4.9 Особенности переходов, в зависимости от свойств параметрического множества
Если параметрическое множество не упорядочено, то понятие параметрического соседства не определено, и, следовательно, существует только одна осмысленная маска. Эта маска, определяемая тождественным правилом сдвига; она называется маской без памяти. Поскольку в этом случае имеется только одна приемлемая маска, задача оказывается довольно тривиальной [требования 3, 4 и 5 просто неприменимы]. Эта задача сводится к определению для заданных данных функции распределения вероятностей, удовлетворяющих требованию 2. Она решается полным перебором данных с помощью маски без памяти (в данном случае порядок выбора не важен) и определения для каждого состояния выборочных переменных с (в данном случае они совпадают с основными переменными) числа N(c) их появлений в данных. Числа N (с) для всех  обычно называются частотами состояний с. Они используются для вычисления по некоторым правилам соответствующих функций вероятностей или возможностей.
обычно называются частотами состояний с. Они используются для вычисления по некоторым правилам соответствующих функций вероятностей или возможностей.
Вычислять распределение вероятности по частотам можно разными способами. Так, например, если вероятности рассматриваются как характеристики данных, то обычно вычисляются относительные частоты, т. е. отношения N(c) к общему числу имеющихся выборок из данных по используемой маске. Отсюда
 .(4.33)
.(4.33)
Помимо реализации разных вариантов вычисления распределения вероятностей необходимо также включать в вычисление некую дополнительную информацию, связанную с ограничениями на переменные. Будем эту информацию, не входящую в собственно данные, называть дополнительной. Она может принимать самые разные формы.
Предположим теперь, что параметрическое множество полностью упорядочено. В этом случае из одной и той же системы данных можно получить множество систем с поведением, отличающимся масками. Если для заданных данных они определены достаточно корректно, то они одинаково хорошо отвечают требованию согласованности. Точнее, выражение «достаточно корректно» означает, что функция поведения хорошо согласуется с данными (и, возможно, с некоторой дополнительной информацией) с точки зрения маски и типа выбранных ограничений.
Как уже объяснялось выше, для маски без памяти функцию поведения, хорошо согласующуюся с данными и дополнительной информацией, можно получить из частот состояний (т. е. соответствующих выборочных переменных) для данных, отображенных с помощью рассматриваемой маски. Всякая маска представляет собой некоторое окно, через которое отбираются рассматриваемые данные из матрицы данных (или из массива более высокого порядка). При движении этого окна вдоль всей матрицы данных частоты состояний соответствующих выборочных переменных определяются подсчетом того, как часто наблюдается каждое состояние. Если все выборочные позиции перебираются, то направление движения маски по матрице данных не имеет значения, однако удобнее осуществлять это движение в соответствии с установленным на параметрическом множестве порядком (слева направо или наоборот).
Для конкретных целей одни маски могут подходить лучше, чем другие, но никакая маска не является правильной или неправильной.
4.10 Особенности построения масок
Если рассматриваемая маска представляет собой один столбец (маска без памяти), то выборки по всем значениям параметра являются полными. Однако, если маска состоит из более чем одного столбца, то некоторые выборки в начале и конце параметрического множества (левый и правый края матрицы данных) окажутся неполными (см. рис. 4.2 и 4.3). Точнее, число неполных выборок для каждого края матрицы данных равно числу столбцов в маске минус 1. Число столбцов в маске М будем называть глубиной маски и обозначать  . Тогда
. Тогда
 ,(4.34)
,(4.34)
где операторы max и min применены ко всем целым  . Так, например, для маски, определенной на рис. 4.1,
. Так, например, для маски, определенной на рис. 4.1,  , для масок без памяти
, для масок без памяти  .
.
Есть два соображения, по которым применение масок с большой глубиной в общем случае нежелательно.
1. если маска используется для порождения данных, то чем больше ее глубина, тем большее требуется начальное условие. Это, вообще говоря, не желательно.
2. если маска используется для выборки данных, то число неполных выборок равно  . Это означает, что с ростом глубины маски все меньше имеющихся данных используется для определения функции поведения. Следовательно, с увеличением глубины маски сужается эмпирическая основа, на которой строится функция поведения. Это, разумеется, также нежелательно.
. Это означает, что с ростом глубины маски все меньше имеющихся данных используется для определения функции поведения. Следовательно, с увеличением глубины маски сужается эмпирическая основа, на которой строится функция поведения. Это, разумеется, также нежелательно.
Оба эти соображения, а также практические соображения, связанные со сложностью вычислений, приводят к тому, что глубина маски обычно выбирается не очень большой. Таким образом, представляется целесообразным определить ограниченность глубины маски как требование 1 для рассматриваемого типа задач. Это можно сделать, определив наибольшую допустимую маску, скажем маску М как декартово произведение
 ,(4.35)
,(4.35)
где  .
.
Подобная маска может быть представлена в виде полной матрицы с п строками и  столбцами. Будем называть ее М-матрицей. Если изначально задано только
столбцами. Будем называть ее М-матрицей. Если изначально задано только  , но не конкретные значения
, но не конкретные значения  и
и , то целесообразно выбирать для них некие стандартные значения, например
, то целесообразно выбирать для них некие стандартные значения, например  , а
, а  .
.
4.11 Содержательные подмаски
При заданной наибольшей допустимой маске М все ее содержательные подмаски образуют ограниченное множество Yr систем с поведением. Термин «содержательная подмаска» характеризует подмаски М, удовлетворяющие следующим требованиям:
(ml) в подмаску входит по крайней мере один элемент из каждой подмаски  , определенной уравнением (4.10) (т. е. один элемент из каждой строки М-матрицы);
, определенной уравнением (4.10) (т. е. один элемент из каждой строки М-матрицы);
(m2) в подмаску должен быть включен по крайней мере один элемент с правилом сдвига  (крайний правый элемент из М-маски).
(крайний правый элемент из М-маски).
Требование ml необходимо для покрытия заданной системы данных, т. е. для того, чтобы гарантировать, что любая базовая переменная из заданной системы данных была бы включена в любую из систем с поведением из ограниченного множества Yr. Требование m2 препятствует дублированию эквивалентных подмасок, т. е. подмасок, преобразуемых одна в другую только с помощью добавления константы к правилу сдвига  (сдвиг ряда в М-маске).
(сдвиг ряда в М-маске).
Можно легко получить формулу для числа  содержательных подмасок наибольшей допустимой маски, где n — число базовых переменных, а
содержательных подмасок наибольшей допустимой маски, где n — число базовых переменных, а  — глубина маски М:
— глубина маски М:
 .(4.36)
.(4.36)
Первый член выражения (4.36) задает число подмасок М, удовлетворяющих условию ml, а второй член — число масок, нарушающих условие m2. В табл. 4.1 приведены значения  при п,
при п,  .
.
Таблица 4.1. Число содержательных масок  , вычисленное по формуле (3.36)
, вычисленное по формуле (3.36)
|
n | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 1 | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 |
| 2 | 1 | 8 | 40 | 176 | 736 | 3,008 | 12,160 | 48,896 | 196,096 | 785,408 |
| 3 | 1 | 26 | 316 | 3,032 | 26,416 | 220,256 |
|
|
|
|
| 4 | 1 | 80 | 2,320 | 48,224 | 872,896 |
|
|
|
|
|
| 5 | 1 | 242 | 16,564 | 742,568 |
|
|
|
|
|
|
| 6 | 1 | 728 | 116,920 |
|
|
|
|
|
|
|
| 7 | 1 | 2,186 | 821,356 |
|
|
|
|
|
|
|
| 8 | 1 | 6,560 |
|
|
|
|
|
|
|
|
| 9 | 1 | 19,682 |
|
|
|
|
|
|
|
|
| 10 | 1 | 59,048 |
|
|
|
|
|
|
|
|
Эта таблица разделена на три области, для которых размеры наибольшей допустимой маски представляются: а) легко поддающимися вычислительной обработке (левая верхняя область); б) в принципе поддающимися обработке, что потребует длительной работы очень мощного компьютера (средняя область); в) неподдающимися вычислительной обработке (правая нижняя область). Эти области показаны только для наиболее типичного случая. Так, например, если имеется в распоряжении мощная система параллельных вычислений, то область случаев, поддающихся вычислительной обработке, может быть расширена почти вдвое.
Если число содержательных масок оказывается слишком велико, чтобы поддаваться вычислительной обработке, АСНИ должны учитывать возможные дополнительные ограничения, накладываемые на наибольшую допустимую маску. Такими ограничениями могут быть, например, следующие:
1. фиксация множества порождаемых выборочных переменных;
Люди также интересуются этой лекцией: 3. Управление ЧС.
2. фиксация числа выборочных переменных;
3. фиксация верхней границы числа выборочных переменных;
4. ограничение, при котором рассматриваются талько маски без пропусков (примером пропуска является элемент, идентифицируемый координатами  ,
,  в маске, изображенной на рис. 4.1,а).
в маске, изображенной на рис. 4.1,а).
Подобные ограничения или их комбинации существенно сокращают множество  , и таким образом, увеличивают размер наибольших допустимых масок, поддающихся вычислительной обработке.
, и таким образом, увеличивают размер наибольших допустимых масок, поддающихся вычислительной обработке.
К.Р. № 12
Исходя из некоторой системы данных, построить функцию поведения, в случае масок без памяти.