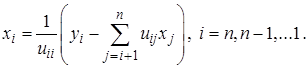Разложение Холецкого
5.2 Разложение Холецкого.
Справедлива следующая теорема (Холецкий).
Для симметричной положительно определенной матрицы  существует единственное разложение
существует единственное разложение  , причем диагональные элементы множителей положительны.
, причем диагональные элементы множителей положительны.
Укажем способ вычисления коэффициентов треугольных множителей.
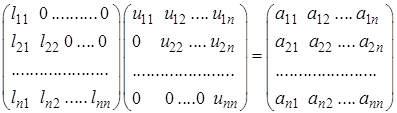
В индексах это равенство имеет вид
 ,
,
откуда следует
 (4)
(4)
Рекомендуемые материалы
Впрочем, эта формула верна и при  , но в этом случае ее надо читать так:
, но в этом случае ее надо читать так:
 (5)
(5)
Из-за формулы (5) метод разложения Холецкого иногда называют методом квадратного корня. Порядок вычислений коэффициентов следующий. Последовательно для строк i=1,2,…,n вначале вычисляется диагональный элемент (5), а затем и все другие коэффициенты  в этой строке по формуле (4). При подсчете
в этой строке по формуле (4). При подсчете  фактически скалярно перемножаются два «надстолбца» с номерами
фактически скалярно перемножаются два «надстолбца» с номерами  (он располагается над диагональным элементом
(он располагается над диагональным элементом  ) и
) и  (он располагается над текущим элементом
(он располагается над текущим элементом  ). Все элементы этих «надстолбцов» уже вычислены.
). Все элементы этих «надстолбцов» уже вычислены.
Рекомендуем посмотреть лекцию "12 Системы индексов".
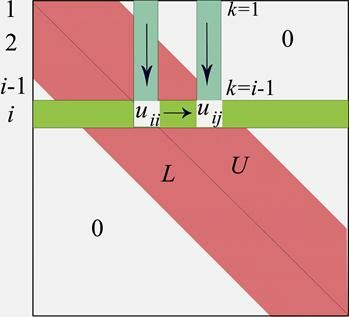
Формулы разложения Холецкого (5), (4) записаны в общем виде для произвольной (заполненной) матрицы. Однако сеточные схемы порождают разреженные матрицы, т.е. такие, у которых подавляющее большинство элементов равны нулю. Главным отрицательным свойством факторизации Холецкого служит заполнение , которое выражается в том, что у треугольных множителей  появляются ненулевые элементы в тех позициях, где у исходной матрицы
появляются ненулевые элементы в тех позициях, где у исходной матрицы  были нули. Это катастрофически увеличивает как требуемый объем памяти для хранения множителей, так и количество вычислений по формулам вида (2), (3). При специальной нумерации узлов сетки можно добиться того, чтобы все ненулевые элементы матрицы
были нули. Это катастрофически увеличивает как требуемый объем памяти для хранения множителей, так и количество вычислений по формулам вида (2), (3). При специальной нумерации узлов сетки можно добиться того, чтобы все ненулевые элементы матрицы  располагались вблизи главной диагонали. В этом случае говорят о ленточной матрице. Вводится понятие ширины ленты. Для произвольной строки
располагались вблизи главной диагонали. В этом случае говорят о ленточной матрице. Вводится понятие ширины ленты. Для произвольной строки  можно указать такой номер столбца
можно указать такой номер столбца  , что все
, что все  при
при  . Полушириной ленты называют значение
. Полушириной ленты называют значение  . Сама лента показана на рисунке розовым цветом. Вне ленты находятся только нулевые элементы, а внутри ее могут быть как ненулевые, так и равные нулю. Алгоритм построения треугольных множителей через скалярное произведение «надстолбцов» показывает, что заполнение при разложении Холецкого ленточной матрицы происходит лишь внутри ленты.
. Сама лента показана на рисунке розовым цветом. Вне ленты находятся только нулевые элементы, а внутри ее могут быть как ненулевые, так и равные нулю. Алгоритм построения треугольных множителей через скалярное произведение «надстолбцов» показывает, что заполнение при разложении Холецкого ленточной матрицы происходит лишь внутри ленты.
Итак, найдена верхняя треугольная матрица  . Чтобы получить решение задачи
. Чтобы получить решение задачи  вначале решаем задачу
вначале решаем задачу  . Однако в симметричном случае саму матрицу
. Однако в симметричном случае саму матрицу  вычислять не обязательно, достаточно в формуле (3) заменить
вычислять не обязательно, достаточно в формуле (3) заменить  на
на  :
:

Затем строим решение исходной задачи, решая систему  , см. (2) :
, см. (2) :