Силы давления жидкости

2. Силы давления жидкости на твердые поверхности

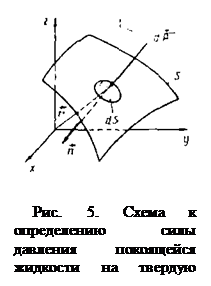
В общем случае воздействие жидкости на твердую поверхность S сводится к сумме элементарных сил , действующих на малых площадках dS, составляющих эту поверхность (рис. 5).

Если  – единичный вектор нормали к поверхности S, внешней к объему жидкости, а – давление на площадке dS, то сила .

Суммируя систему сил , получаем выражение для главного вектора

,                                                                      (46)

называемого силой давления жидкости на поверхность S, и выражение для главного момента

,                                                                (47)

где  – радиус-вектор площадки  относительно центра приведения системы сил.

Рассмотрим несколько частных случаев.

Рекомендуемые материалы

2.1. Равномерное давление на плоскую стенку (р=const., п=const).

В этом случае суммируемые векторы  составляют систему параллельных и одинаково направленных сил. Такая система всегда может быть сведена только к силе давления . При р = const и n = const из выражения (46) получаем

.               (48)

Линия действия силы  проходит через центр тяжести площади S.

Равномерное давление может создаваться покоящимся газом, так как благодаря малой его плотности можно  пренебречь  действием массовых сил и считать давление одинаковым во      всех точках газа.

Равномерное давление может создаваться и капельной жидкостью, например, при ее воздействии на горизонтальные площадки, в случае абсолютного покоя или движения сосуда с ускорением вверх или вниз.

Величина силы  при равномерном распределении давления не зависит от ориентации плоской стенки S в пространстве и вычисляется по формуле .

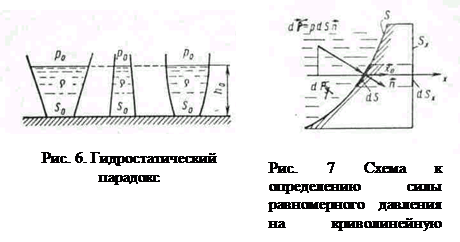
Например, для схемы на рис. 6 давление на дне , а сила . Заметим, что сила давления на дно не зависит от формы сосуда (гидростатический парадокс).

2.2. Сила равномерного давления на криволинейную стенку (, )

В этом случае элементарные силы  имеют разные направления. Главный вектор  системы вычисляется через свои проекции. Чтобы найти его проекцию  на ось х , проектируем на эту ось векторы  (рис.7).

,

где  – единичный вектор оси x; – проекция площадки dS на плоскость, нормальную оси х. Искомая величина  при

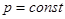
.                                 (49)

Линия действия силы  проходит через центр тяжести площади проекции . Таким образом, величина проекции на направлении оси x силы равномерного давления р на криволинейную поверхность S равна произведению давления и площади проекции S_x этой криволинейной поверхности на плоскость. нормальной оси х. Если такие проекции на три взаимно ортогональные оси пересекаются в одной точке, то система сил  может быть сведена только к силе давления, величина которой

,                                                        (50)

а направление определяется направляющими косинусами

; ; .                        (51)

Если составляющие не пересекаются в одной точке, система сводится к силе и моменту.

2.3. Сила неравномерного давления на плоскую стенку (, ).

Систему элементарных сил , одинаковых по направлению, но различных по величине, можно свести в данном случае к одной силе давления

,                                                                      (52)

где S – площадь стенки.

Величина этой силы

                                                             (53)

зависит от закона распределения давления Р по площади S. При воздействии на S капельной жидкости эти законы могут быть различными. Их конкретный вид зависит от ориентации площадки и действующих на жидкость массовых сил при абсолютном и относительном покое.

Вычислим силу  для плоской стенки, наклоненной к горизонту под углом a и подверженной  воздействию  тяжелой жидкости, находящейся в состоянии абсолютного покоя (рис. 8).

Определим результирующую силу избыточных давлений , которые создаются внешним избыточным  и весовым  давлениями. Заменим внешнее давление  воздействием эквивалентного слоя жидкости, толщина, которого  определяется высотой поднятия жидкости в пьезометре . Таким образом, внешнее давление из рассмотрения исключается, и свободная поверхность СП заменяется пьезометрической плоскостью ПП. Продолжим плоскость стенки до пересечения с пьезометрической плоскостью. Вдоль линии их пересечения направим ось х, а ось у расположим в плоскости стенки. Затем для наглядности повернем плоскость стенки на 90° вокруг оси у и совместим стенку с плоскостью чертежа.

Величину силы вычислим по формуле (53):

.

В рассматриваемом случае (см. рис. 8) давление

,                                                     (54)

что при подстановке в формулу (53) дает

.

Интеграл  представляет собой статический момент площади S относительно оси Ох, равный, как известно, произведению S на координату  ее центра тяжести.

Поэтому

.                (55)

Формула (55) может быть записана в двух видах

,                                                                          (56)

где  – избыточное давление в центре тяжести площади S, или

.                                                           (57)

Согласно (56) величина силы избыточного давления покоящейся жидкости на плоскую стенку равна произведению площади стенки на избыточное давление в ее центре тяжести.

Вектор силы  направлен по нормали к стенке S:

,

а линия действия этой силы пересекает стенку в некоторой точке D, называемой центром давления. Для отыскания координат этой точки () используем теорему о равенстве момента равнодействующей и суммы моментов составляющих, которая в данном случае выражается уравнением

,                                                         (58)

где  и  – радиус-векторы соответственно центра давления D и произвольной точки (ху) площади S.

По правилам составления проекций векторного произведения находим

; .

Учитывая выражения (54) и (55), получим

                                                                     (59)

Более удобные выражения для  и  получим, если воспользуемся теоремой о соотношении между моментами второй степени, взятыми относительно параллельных осей

; ,

где – оси координат, проходящие через центр тяжести С площадки S параллельно осям х и у;  и  – координаты центра тяжести С в системе xу;  – центробежный момент площади S относительно осей х и у ;  – момент инерции площади S относительно оси х (см. рис. 8). Окончательно,

; .                                     (60)

Вторая из формул (60) показывает, что центр давления расположен ниже центра тяжести на величину .

Возвращаясь к формуле (57), заметим, что силу давления в рассматриваемом случае можно получить, складывая независимо вычисленные две силы:  и , где – сила внешнего избыточного давления, – сила весового давления. При таком способе определения силы  следует помнить, что линии действия сил  и  не совпадают, и центр давления D определяется линией действия суммарной силы .

2.4. Неравномерное давление на криволинейную твердую поверхность (, ) может быть создано тяжелой жидкостью при абсолютном или относительном покое. Элементарные силы  составляют в этом случае самую общую систему, которая должна сводиться к силе давления  (46) и моменту  (47). Однако существуют частные случаи,, когда система сводится к одной силе давления , например, если линии действия элементарных сил  пересекаются в одной точке (сферическая стенка).

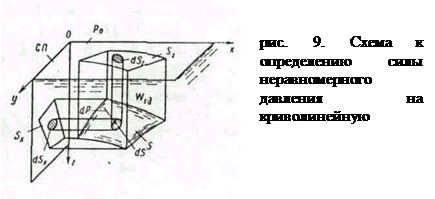
Рассмотрим криволинейную поверхность S, находящуюся под воздействием внешнего избыточного давления  и весового давления  (рис.9). Как было показано в предыдущем пункте, задачу отыскания силы давления можно расчленить, определяя раздельно силы весового и внешнего давлений. Эту же задачу можно свести к задаче об определении только весового давления, заменив внешнее давление действием эквивалентного слоя жидкости.

Силу весового давления  определим по ее проекциям. Горизонтальная проекция

,

где  – проекция площадки dS на вертикальную плоскость, нормальную к оси х. Последний интеграл представляет  собой  статический  момент площади  относительно оси y. Следовательно,

,                                                                   (61)

где – координата центра тяжести площади .

Аналогично получим

,                                                                   (62)

где – площадь проекции криволинейной поверхности на плоскость, нормальную оси y.

Таким образом, чтобы вычислить горизонтальную проекцию  силы весового давления на криволинейную поверхность, следует площадь проекции  этой поверхности на плоскость, нормальную к рассматриваемой горизонтальной оси, умножить на давление в центре тяжести площади .

Проекция силы весового давления на вертикальную ось определится соотношением

,                                    (63)

где – проекция на плоскость х0у поверхности S.

Последний интеграл представляет собой объем тела , ограниченного поверхностью S, цилиндрической боковой поверхностью  с вертикальными образующими и проекцией  криволинейной поверхности S на свободную поверхность жидкости. Это тело называется телом давления, а величина  есть вес жидкости в его объеме.

Таким образом, вертикальная проекция силы весового давления на криволинейную поверхность равна весу жидкости в объеме тела давления.

Величина  силы  определится формулой

,                                                         (64)

а направление линии ее действия – направляющими косинусами

; ; .                    (65)

Если ,  и  пересекаются в одной точке, то система сводится к силе давления, проходящей через эту точку.

В лекции "Лекция №8 Правовые и организационные основы безопасности" также много полезной информации.

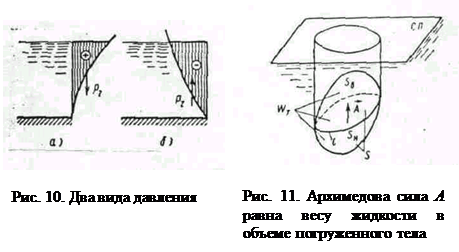
Возможны два случая расположения криволинейной поверхности (рис. 10 а и б) под уровнем жидкости. В первом случае жидкость расположена над твердой поверхностью; тело давления заполнено жидкостью и считается положительным, а вертикальная составляющая силы направлена вниз. Во втором случае тело давления не заполнено жидкостью и считается отрицательным; вертикальная сила давления направлена вверх.

Если криволинейная поверхность S замкнута и полностью погружена под уровень абсолютно покоящейся жидкости (рис. 11), то воздействие жидкости сводится к одной вертикальной силе. Действительно, для любой горизонтальной оси существуют две противоположно направленные и равные по величине силы, действующие на тело; поэтому результирующая горизонтальных сил равна нулю. Чтобы найти вертикальную силу, проектируем S на свободную поверхность жидкости. Проектирующие вертикали отметят на поверхности тела замкнутую линию l, которая делит поверхность на две части  и . Для верхней части  тело давления положительно и соответствующая ему сила направлена вертикально вниз, а для нижней  – тело давления отрицательно и сила направлена вверх. Обозначив объемы этих тел давления соответственно через  и , найдем величину результирующей вертикальной силы А:

,                                                 (66)

где – объем тела.

Таким образом, сила давления покоящейся жидкости на погруженное в нее тело направлена вертикально вверх и равна весу жидкости в объеме тела. Этот результат составляет содержание закона Архимеда: сила А называется архимедовой или гидростатической подъемной силой. Если G – вес тела, то его плавучесть определяется соотношением сил А и G. При  тело тонет, при  – всплывает, при G = А – плавает в состоянии безразличного равновесия. Следует иметь в виду, что линии действия сил G и А могут не совпадать, так как линия действия веса G проходит через центр тяжести тела, а линия действия архимедовой силы А – через центр его объема. При неравномерном распределении плотности тела может появиться момент, способствующий опрокидыванию тела.

В заключение отметим, что сила давления жидкости по криволинейной поверхности в случаях относительного покоя может быть определена общим способом суммирования элементарных сил давления, применительно к заданной форме поверхности и условиям относительного покоя.