Статически определимые фермы
Основные понятия и определения.
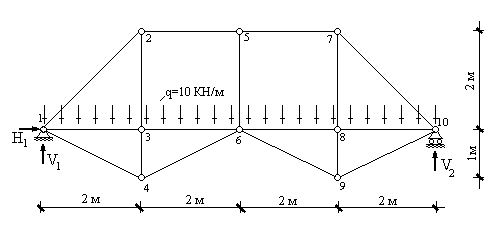
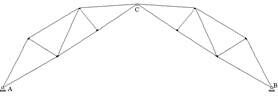
Ферма - такая стержневая система, которая сохраняет геометрическую неизменяемость в случае если во всех местах соединения ее стержней (узлах фермы) врезать шарниры (рис.1). Стержни, представляющие собой верхнюю часть контура фермы, называют верхним поясом фермы, нижнюю часть - нижним поясом фермы. Расстояние между двумя соседними узлами любого из поясов фермы называется панелью фермы. Вертикальные стержни в ферме называют стойками, наклонные - раскосами. Совокупность раскосов и стоек образует решетку фермы.
|
|
|
Рис. 2 |
|
Рис. 3 |
В зависимости от конфигурации решетки различают фермы различных типов. Наиболее распространенными являются раскосные фермы (рис.2) и фермы с треугольной решеткой (рис.3). Раскосы, идущие вверх от опор к середине фермы, называют восходящими раскосами (рис.1), идущие наоборот - нисходящими раскосами (рис.2). Фермы, усиленные дополнительными стержнями (шпренгелями), называют шпренгельными фермами (рис.4).
Фермы, как правило, проектируют таким образом, чтобы основная нагрузка на них передавалась через узлы верхнего или нижнего пояса. Наличие шпренгелей позволяет увеличить количество узлов в этом поясе, что может потребоваться для облегчения конструкций, с помощью которых внешняя нагрузка передается на узлы фермы или, например, для уменьшения ширины плит перекрытий, опирающихся на стропильные фермы здания. (рис.5).
|
|
|
|
|
Рис. 7 |
|
Рис. 9 |
|
Рис. 10 |
|
Рис. 8 |
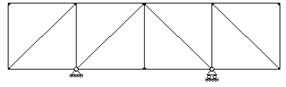
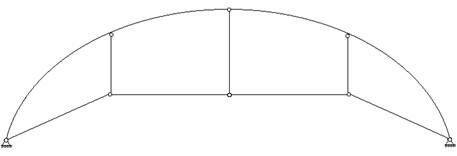
В зависимости от характера опорных закреплений различают балочные фермы (рис.6), консольные фермы (рис.7), консольно-балочные фермы (рис.8) и арочные фермы (рис.9). Кроме того, отдельно рассматриваются различные висячие системы (рис.10) и комбинированные системы (рис.11).
|
Рис. 11 |
Если нагрузка на узлы верхнего или нижнего пояса фермы подвижная, например от действия движущегося подвижного состава в фермах пролетных строений мостов, то этот пояс фермы называют ездовой линией или проезжим поясом.
В качестве расчетной схемы фермы применяют шарнирную схему, в которой все узлы фермы считаются идеальными шарнирами.
Фермы используются в качестве пролетных строений мостов, стропильных конструкций зданий, опор линий элекропередач, радио- и телемачт, каркасов зданий, а также в различных машиностроительных конструкциях, например, в качестве стрел подъемных кранов.
Статическая работа ферм.
Фермы часто используются для перекрытия пролетов, т.е. имеют такое же назначение, что и балки сплошного сечения.
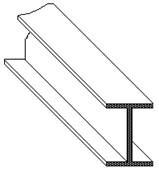
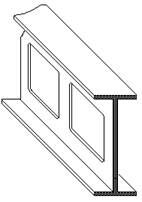
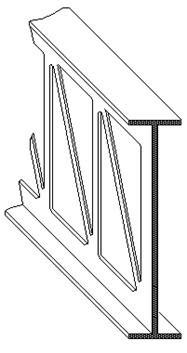
Известно, что при изгибе балки нормальные напряжения в ее поперечных сечениях достигают максимальных значений в верхних и нижних точках сечения. Желание использовать материал балки наиболее экономичным образом заставляет сосредотачивать большую часть материала в наиболее напряженных зонах, что достигается применением балок двутаврового поперечного сечения (рис.12). При увеличении пролета и нагрузок высоту балки приходится увеличивать. Следовательно, количество материала в стенке, где напряжения малы, будет расти. Это приведет не только к перерасходу материала в малозагруженной зоне, но и значительно увеличит собственный вес конструкции. Поэтому для экономии материала и облегчения конструкции в вертикальной стенке устраивают вырезы (рис.13). С дальнейшим ростом пролета и нагрузок высота сечения конструкции еще увеличивается, и стенка двутавра постепенно переходит в систему стоек. Для того, чтобы полученная конструкция сохраняла геометрическую неизменяемость, т.е. не “сложилась” при действии горизонтальных нагрузок, к системе стоек добавляют систему раскосов, в результате чего и образуется решетка фермы (рис.14).
|
Рис. 12 |
|
Рис. 13 |
|
Рис. 14 |
Таким образом, фермы могут быть использованы для перекрытия больших пролетов при действии высоких нагрузок, когда использование балок сплошного сечения оказывается невыгодным или невозможным.
Как и при изгибе балки на двух опорах под действием нагрузки, направленной вниз, стержни верхнего пояса балочной фермы будут сжатыми, а нижнего - растянутыми. В консольной ферме (рис.7) ситуация будет обратной.
Узлы фермы, как правило, конструктивно выполняются жесткими. Однако, как показал опыт расчетов, напряжения в стержнях ферм, определенные с учетом жесткости узлов, и напряжения, определенные по шарнирной схеме, обычно отличаются не более, чем на несколько процентов. Поскольку выполнять расчет во втором случае значительно легче, жесткостью узлов фермы пренебрегают и расчет ведут по шарнирной схеме. Иными словами, при расчете фермы все ее узлы считают идеальными шарнирами.
|
Рис. 15 |
Если все нагрузки на ферму приложены исключительно к узлам, а стержни ферм являются прямыми, то в стержнях ферм действуют только продольные усилия, а изгибающие моменты и перерезывающие усилия отсутствуют. Действительно, вырежем мысленно любой стержень из фермы, заменив действие остальных стержней на него усилиями, передаваемыми через шарниры (рис.15). Поскольку других нагрузок на стержень нет, равнодействующие этих сил должны быть направлены по оси стержня. Если бы это было не так, стержень не мог бы находиться в равновесии, в чем легко убедиться, составив уравнение моментов относительно любого из шарниров. Очевидно, единственным усилием, которое в этом случае будет возникать в стержне, будет постоянное по его длине продольное усилие.
Геометрическая неизменяемость ферм.
Для обеспечения геометрической неизменяемости необходимо, во-первых, чтобы связей, наложенных на перемещение узлов фермы было достаточно, во-вторых, они были правильно размещены. Следовательно, исследование геометрической неизменяемости фермы состоит из двух шагов: проверки достаточности числа связей и анализе правильности их размещения (структурном анализе фермы).
Как обычно, при анализе геометрической неизменяемости смещения, вызванные деформированием стержней в расчет не берутся. Иными словами, при анализе геометрической неизменяемости ферм, как и любых других стержневых систем, будем считать стержни абсолютно жесткими.
Каждый узел плоской фермы имеет две степени свободы, т.е. имеет возможность линейного смещения, например, в вертикальном и горизонтальном направлениях. Следовательно, минимальное количество связей, необходимых для закрепления узлов фермы от смещений, должно равняться удвоенному числу узлов. Часть из этих связей должна обеспечивать закрепление фермы относительно основания. Таким образом, минимальное число стержней в ферме, необходимое для обепечения ее геометрической неизменяемости определяется по формуле:
|
| (1) |
где  -число стержней в ферме,
-число стержней в ферме,  - число узлов , а
- число узлов , а  -число опорных связей.
-число опорных связей.
Условие (1) одновременно является условием статической определимости фермы. Действительно, для каждого узла можно составить два уравнения равновесия- условия равенства нулю проекций на вертикальную и горизонтальную оси всех действующих на узел внешних сил и сил, действующих со стороны стержней и реакций опор. Неизвестными же являются продольные усилия в каждом стержне и реакции в опорах. Записав все эти  уравнений, получим систему уравнений, которую в матричной форме можно записать в виде:
уравнений, получим систему уравнений, которую в матричной форме можно записать в виде:
| AX=B, | (2) |
где Х - вектор неизвестных усилий в стержнях и опорных связях, В - вектор проекций внешних нагрузок на узлы, А-матрица системы.
Для того, чтобы система (2) была замкнутой, необходимо чтобы число уравнений  совпадало с числом неизвестных, т.е. выполнялось условие (1).
совпадало с числом неизвестных, т.е. выполнялось условие (1).
Если количество стержней в ферме будет больше, чем требуется согласно (1), то ферма будет статически неопределимой, если меньше - то геометрически изменяемой.
При этом, важно отметить, что условие (1) является необходимым, но не достаточным для обеспечения геометрической неизменяемости. Как уже упоминалось, кроме обеспечения необходимого числа связей, требуется их правильное размещение.
|
Рис. 16 |
Систему, в которой невозможны взаимные смещения узлов, в предположении, что все стержни абсолютно жесткие, называют жестким диском. В шарнирном треугольнике (например, ABC на рис.16) взаимное смещение узлов будет невозможным, следовательно он является жестким диском. Присоединение к такому треугольнику еще одного узла двумя не лежащими на одной прямой связями приведет к образованию системы, в которой также взаимные смещения узлов будут невозможны. Если продолжить этот процесс, то полученная система также будет жеским диском. Примером жесткого диска является простейшая ферма, т.е. ферма, состоящая из шарнирных треугольников (рис.16). Взаимные смещения узлов в такой фермы невозможны. Остается только позаботиться о прикреплении полученной простейшей фермы к основанию.
Для того, чтобы обеспечить неподвижность простейшей фермы относительно основания, необходимы как минимум три опорных связи, линии действия которых не параллельны и не пересекаются в одной точке.
Рассмотрим в качестве примера ферму, изображенную на рис.1. Очевидно, она относится к простейшим фермам. В ней  ,
,  ,
, . Равенство (1) выполняется: 25=2×14-3=25. Линии действия трех опорных связей (опорных реакций на рис.1) не параллельны и не пересекаются в одной точке, следовательно ферма геометрически неизменяема.
. Равенство (1) выполняется: 25=2×14-3=25. Линии действия трех опорных связей (опорных реакций на рис.1) не параллельны и не пересекаются в одной точке, следовательно ферма геометрически неизменяема.
Теперь выполним перестановку опорных связей. Отбросим на левой опоре одну связь, сделав неподвижную опору катковой, но добавим еще одну катковую опору в центре пролета фермы (рис.17).
|
Рис. 17 |
В результате, количество опорных связей не изменилось, а осталось равным трем, т.е. равенство (1) осталось справедливым. Однако линии действия опорных связей стали параллельными - направленными вертикально вверх. В результате система получила возможность смещения в горизонтальном направлении, т.е. стала геометрически изменяемой.
|
Рис. 18 |
Если же в ферме, изображенной на рис.1, выполнить перестановку стержней, как показано на рис.18, равенство (1) останется неизменным, но система окажется геометрически изменяемой за счет неправильного распределения связей. Это очевидно, т.к. шарнирами C, D, E и F образуется шарнирный квадрат, который при приложении малейшей нагрузки обращается в ромб.
Если ферма образована из двух жестких дисков, то для того, чтобы исключить взаимные смещения узлов в полученной системе, необходимо, чтобы они соединялись между собой как минимум тремя связями, линии действия которых не параллельны и не пересекаются в одной точке.
В ферме на рис.18 два жестких диска ABCD (он представляет собой простейшую ферму) и FEGH (ферма, образованная из простейшей добавлением одной “лишней” связи) соединются между собой только двумя связями DF и CE, что и приводит к геометрической изменяемости фермы, в чем мы уже убедились.
Рассмотрим арочную ферму, изображенную на рис.9. Здесь  ,
,  ,
, . Условие (1) выполняется: 18=11×2-4=18. Эта ферма также образована двумя жесткими дисками (простейшими фермами). Они соединяются между собой шарниром С, т.е., на первый взгляд, только двумя связями, т.к. шарнир препятствует взаимному смещению соединяемых им узлов в вертикальном и горизонтальном направлениях. Однако, поскольку опоры А и В неподвижны, взаимных горизонтальных смещений точек А и В быть не может. Значит, роль третьей связи играет основание. Поэтому рассматриваемая система геометрически неизменяема, а в обеих опорах возникнут горизонтальные распорные реакции.
. Условие (1) выполняется: 18=11×2-4=18. Эта ферма также образована двумя жесткими дисками (простейшими фермами). Они соединяются между собой шарниром С, т.е., на первый взгляд, только двумя связями, т.к. шарнир препятствует взаимному смещению соединяемых им узлов в вертикальном и горизонтальном направлениях. Однако, поскольку опоры А и В неподвижны, взаимных горизонтальных смещений точек А и В быть не может. Значит, роль третьей связи играет основание. Поэтому рассматриваемая система геометрически неизменяема, а в обеих опорах возникнут горизонтальные распорные реакции.
Выполним перестановку связей в этой ферме. Сделаем одну из опор катковой, сняв таким образом ограничение на взаимные горизонтальные смещения точек А и В. Однако, добавим стержень, который возьмет на себя роль третьей связи, соединяющей простейшие фермы (рис.19). Равенство (1) при этом не нарушится: 19=11×2-3=19, система останется геометрически неизменяемой, а роль основания по восприятию горизонтального усилия перейдет введенному стержню, работающему в качестве затяжки.
|
Рис. 19 |
|
Рис. 20 |
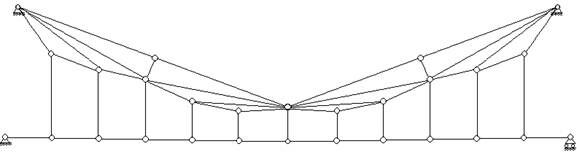
В качестве еще одного примера рассмотрим ферму Шухова[1] (рис.20). В ней  ,
,  ,
, . Условие (1) выполняется: 9=6×2-3=9.
. Условие (1) выполняется: 9=6×2-3=9.
Ферма образована двумя шарнирными треугольниками ABC и DEF, связанными между собой тремя связями- AF, BE, и DC, линии действия которых не параллельны и не пересекаются в одной точке. Прикрепление образованного в результате жесткого диска к основанию выполнено при помощи одной неподвижной и одной катковой опоры, т.е. также при помощи трех связей, линии действия которых не параллельны и не пересекаются в одной точке. Следовательно, ферма геометрически неизменяема.
В случаях, когда простым структурным анализом не удается доказать геометрическую неизменяемость фермы, приходится пользоваться более сложными методами. Одним из них является статический метод анализа геометрической неизменяемости ферм. Идея метода заключается в следующем. Для геометрически изменяемой фермы система уравнений (2) не должна иметь решений, следовательно матрица А должна быть особенной, т.е. ее определитель должен быть равен нулю. Как известно, если в однородной системе линейных алгебраических уравнений АХ=0 определитель матрицы А равен нулю, то система кроме тривиального решения Х=0 допускает и ненулевое решение. Поэтому, в стержнях статически определимой, но геометрически изменяемой фермы при нулевой нагрузке может возникнуть система самоуравновешенных сил.
Для того, чтобы доказать геометрическую неизменяемость фермы, необходимо доказать, что при отсутствии внешней нагрузки в ее стержнях не может возникнуть усилий. Если же оказывается, что при отсутствии нагрузки в стержнях фермы могут существовать ненулевые усилия, то это указывает на равенство определителя матрицы А нулю, а значит и на геометрическую изменяемость фермы.
При выполнении анализа подобного рода, как и при выполнении статического расчета фермы, оказываются полезными правила определения нулевых стержней. Нулевым стержнем называется стержень, в котором при рассматриваемой нагрузке усилие равно нулю. Приведем эти правила.
|
Рис. 21 |
1. Если в незагруженном узле под углом соединяются два стержня, то оба стержня - нулевые (рис.21). В этом легко убедиться, составив уравнения проекций сил на оси, совпадающие с направлением стержней.
|
Рис. 22 |
2. Если в незагруженном узле сходятся сходятся три стержня, причем два лежат на одной прямой, то третий стержень - нулевой (рис.22). В этом легко убедиться, составив уравнение проекций сил на ось, перпендикулярную двум стержням, лежащим на одной прямой.
|
Рис. 23 |
3. Если к узлу, в котором сходятся два стержня, приложена сила, направление действия которой совпадает с одним из них, то второй стержень - нулевой (рис.23). В этом легко убедиться, составив уравнение проекций сил на ось, перпендикулярную линии действия внешней силы.
4. Если в узле сходятся три и более стержней, то те из них, о которых заранее известно, что они являются нулевыми, при определении остальных нулевых стержней и нахождении усилий в стержнях, очевидно, могут быть мысленно отброшены.
5. Если обо всех стержнях кроме одного, сходящихся в незагруженном узле, известно, что они нулевые, то и последний стержень тоже будет нулевым. В этом легко убедиться, составив уравнение проекций сил на ось, совпадающую с направлением этого стержня.
Рассмотрим в качестве примера ферму, изображенную на рис.24.
|
Рис. 24 |
Для нее  ,
,  ,
, . Условие (1) выполняется: 22=15×2-8=22. Сделать вывод о ее геометрической неизменяемости на основе структурного анализа не удается, поэтому приходится пользоваться статическим методом анализа геометрической неизменяемости фермы, т.е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отстутсвии внешней нагрузки.
. Условие (1) выполняется: 22=15×2-8=22. Сделать вывод о ее геометрической неизменяемости на основе структурного анализа не удается, поэтому приходится пользоваться статическим методом анализа геометрической неизменяемости фермы, т.е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отстутсвии внешней нагрузки.
Из рассмотрения узлов 5 и 7, согласно признаку 2 нулевых стержней следует, что стержени 3-5 и 7-6 - нулевые. Далее, из рассмотрения узла 3, согласно признакам 4 и 2 следует, что стержень 2-3 нулевой. Далее, из рассмотрения узла 2, согласно признакам 4 и 1 следует, что стержни 1-2 и 2-6 - нулевые. Далее, из рассмотрения узла 6, согласно признакам 4 и 2 следует, что стержень 3-6 нулевой, а значит, в соответствии с признаком 5, нулевым будет и стержень 6-8. Далее, из рассмотрения узла 3, согласно признаку 5 следует, что стержень 1-3 нулевой. Аналогично доказывается, что соответствующие стержни на правой стороне фермы, а именно стержни 8-10, 10-14, 14-15, 9-10, 11-12, 12-14, 10-12 и 12-15 тоже будут нулевыми. Рассмотрим теперь узел 8. В соответствии с признаками 4 и 1 стержень 7-8 будет нулевым. Далее, последовательно рассматривая узлы 7 и 5, пользуясь признаком 5, докажем, что стержни 5-7 и 4-5 - нулевые. Аналогично доказывается, что соответствующие стержни на правой стороне фермы, а именно 8-9, 9-11,11-13, тоже будут нулевыми. Итак, нам удалось доказать, что все стержни фермы при отсутствии нагрузки являются нулевыми. Следовательно, в этом случае в них не может возникнуть ненулевые усилия, а значит ферма геометрически неизменяема.
Теперь рассмотрим ферму, изображенную на рис.25.
|
Рис. 25 |
Для нее  ,
,  ,
, . Условие (1) выполняется: 10=7×2-4=10. Сделать вывод о ее геометрической неизменяемости на основе структурного анализа не удается, поэтому приходится пользоваться статическим методом анализа геометрической неизменяемости фермы, т.е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отстутсвии внешней нагрузки.
. Условие (1) выполняется: 10=7×2-4=10. Сделать вывод о ее геометрической неизменяемости на основе структурного анализа не удается, поэтому приходится пользоваться статическим методом анализа геометрической неизменяемости фермы, т.е. проанализировать возможность существования самоуравновешенной системы усилий в ее стержнях при отстутсвии внешней нагрузки.
Рассмотрим узел 1. Поскольку на него может действовать только вертикальная опорная реакция, в соответствии с признаком 3 нулевых стержней стержень 1-3 является нулевым. Из рассмотрения узла 7 тот же вывод можно сделать о стержне 5-7. Рассмотрим далее узел 3. На основании признаков 2 и 4 нулевых стержней можно заключить, что стержень 3-5 нулевой.
Предположим, что в стержне 1-2 возникло растягивающее усилие N1-2=N. Рассмотрим равновесие узла 2 (рис.26). Составим для него уравнения проекций действующих на узел усилий на вертикальную и горизонтальную оси:  ,
,  , откуда следует, что
, откуда следует, что  , а
, а  . Рассмотрим далее равновесие ула 6 (рис.27). Из аналогичных уравнений равновесия, составленных для этого узла, получим:
. Рассмотрим далее равновесие ула 6 (рис.27). Из аналогичных уравнений равновесия, составленных для этого узла, получим: ,
,  . Отсюда следует, что
. Отсюда следует, что  , а
, а  .
.
|
|
|
Рис. 27 |
|
Рис. 26 |
Рассмотрим далее равновесие опорных узлов. Учитывая отсутствие усилий в стержнях 1-3, 3-5 и 3-7, из рассмотрения равновесия узлов 3 и 5 (из уравнения проекций сил на оси, совпадающие с направлением стержней 2-3 и 6-5) легко заключить, что  и
и  . Из уравнения равновесия проекций сил на вертикальную ось для узла 4 (рис.28), получим:
. Из уравнения равновесия проекций сил на вертикальную ось для узла 4 (рис.28), получим:  , где V4-вертикальная опорная реакция. Отсюда следует, что
, где V4-вертикальная опорная реакция. Отсюда следует, что  .
.
Легко убедиться, что в каждой их двух других опор действует вертикальная реакция величиной N, направленная вверх. Составим для фермы уравнение проекций всех сил на вертикальную ось. Поскольку внешняя нагрузка отсутствует, в него будут входить только опорные реакции. Очевидно, их равнодействующая равна нулю, а значит система находится в равновесии.
Таким образом, мы доказали, что в стержнях фермы при отсутствии внешней нагрузки может иметься система самоурановешенных сил, что говорит о том, что ферма геометрически изменяема.
Если бы в процессе подобных рассуждений мы столкнулись с противоречием (например, невозможностью удовлетворить уравнениям равновесия) или доказали бы, что все стержни фермы - нулевые, то отсюда следовала бы невозможность существования такой системы усилий, а значит ферма была бы геометрически неизменяемой.
Статический расчет фермы
Статический расчет фермы заключается в определении реакций в ее опорах и нахождении усилий в ее стержнях.
Для статически определимых ферм для решения данной задачи, как известно, достаточно только уравнений равновесия. Составив для каждого узла по два уравнения равновесия проекций всех сил на вертикальную и горизонтальную оси, получим замкнутую систему уравнений (2), решив которую найдем усилия во всех стержнях фермы и реакции опор. Данный алгоритм может быть относительно просто реализован в виде программы для ЭВМ. Кроме того, статический расчет фермы может быть выполнен с применением программных комплексов на основе метода конечных элементов, о котором речь пойдет во второй части учебника.
В то же время, при расчете ферм с небольшим количеством стержней, а также при проверке результатов расчетов, полученных на ЭВМ, может потребоваться использование простейших приемов определения усилий в стержнях ферм. К ним относятся вырезание узлов и сечения.
Способ вырезания узлов уже использовался нами при статическом анализе геометрической неизменяемости фермы. Он заключается в мысленном вырезании узла фермы с заменой действия на него стержней соответствующими усилиями. Эти усилия связаны между собой и приложенной к стержню внешней нагрузкой (или опорными реакциями) посредством статических уравнений равновесия. Для любого узла можно составить два таких уравнения - равенства нулю суммы проекций всех сил, например, на вертикальную и горизонтальную оси. Очевидно, если в узле сходятся два стержня (например, рис.21 и рис.23), то из этих уравнений могут быть найдены усилия в обоих из них. Если узел соединяет три стержня, но усилие в одном из них уже найдено из рассмотрения равновесия другого узла или использованием способа сечений, то из этих двух уравнений могут быть найдены усилия в двух оставшихся стержнях.
Способ сечений состоит в мысленном рассечении фермы на две части и рассмотрении равновесия одной из них. При этом действие отбрасываемой части на рассматриваемую должно быть заменено усилиями в стержнях ферм. Если провести сечение таким образом, чтобы оно проходило через три стержня, то можно составить уравнения равновесия для рассматриваемой части фермы таким образом, чтобы найти усилия во всех трех стержнях.
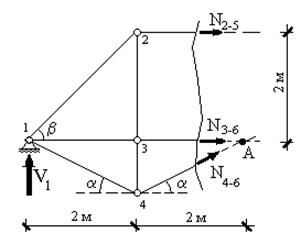
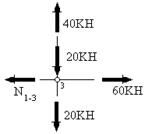
В качестве примера рассмотрим ферму, изображенную на рис.1. Для определения усилия в любом из ее раскосов, а также в любом стержне верхнего или нижнего пояса достаточно провести вертикальное сечение в соответствующей панели фермы и рассмотреть равновесие любой отсеченной части. Очевидно, выгоднее рассматриваить равновесие той части, для которой проще составить уравнение равновесия (рис.29).
|
Рис. 29 |
Если составить уравнение равновесия моментов относительно точки А, то в это уравнение войдет только одно неизвестное усилие - усилие NНП в стержне нижнего пояса. Следовательно, это усилие может быть определено из этого уравнения. Если составить уравнение равновесия моментов относительно точки В, то в это уравнение также войдет только одно неизвестное усилие - усилие NВП в стержне верхнего пояса. Следовательно, это усилие может быть определено из этого уравнения. Если составить уравнение равновесия проекций всех сил на вертикальную ось, то в это уравнение войдет только одно неизвестное усилие - усилие в раскосе NР. Следовательно, это усилие может быть определено из этого уравнения. Для определения усилия в стойке сечение нужно выполнять так, чтобы оно проходило через нее (рис.30).
|
Рис. 30 |
Если составить уравнение равновесия проекций всех сил на вертикальную ось, то в это уравнение войдет только одно неизвестное усилие - усилие в стойке NС. Следовательно, это усилие может быть определено из этого уравнения.
Если в сечение попадает количество стержней превышающее три, то чаще всего приходится комбинировать способ сечений и способ вырезания узлов, определяя усилия в части из стержней в сечении из рассмотрения равновесия узлов или при выполнении других сечений.
Таким образом, усилие в любом стержне статически определимой фермы может быть определено в один или несколько шагов путем последовательных вырезаний узлов и/или рассмотрением равновесия отсеченных определенным образом частей фермы.
Очевидно, при использовании этих способов необходимо предварительное определение опорных реакций из уравнений равновесия фермы.
Пример расчета фермы на неподвижную нагрузку.
Выполним статический расчет фермы, изображенной на рис.31.
|
|
Для данной фермы  ,
,  ,
, . Условие (1) выполняется: 17=10×2-3=17. Следовательно, необходимое условие статической неопределимости и геометрической неизменяемости фермы выполняется.
. Условие (1) выполняется: 17=10×2-3=17. Следовательно, необходимое условие статической неопределимости и геометрической неизменяемости фермы выполняется.
Теперь исследуем правильность расстановки связей в ферме. Данная ферма образована двумя жесткими дисками. Контур первого из них ограничен узлами 1,4,6,5,2. Действительно, жесткий диск образован тремя шарнирными треугольниками, к которым двумя стержнями, не лежащими на одной прямой, присоединен узел 5. Второй диск, контур которого ограничен узлами 6,8,7,10,9, также образован тремя шарнирными треугольниками, т.е. представляет собой простейшую ферму. Два диска соединены между собой тремя связями, линии действия которых не параллельны и не пересекаются в одной точке,- в узле 6 и стержнем 5-7. Таким образом, вся конструкция также представляет собой жесткий диск. Он прикреплен к основанию тремя связями, линии действия которых не параллельны и не пересекаются в одной точке. Следовательно, на основе структурного анализа можно сделать вывод, что данная ферма является геометрически неизменяемой.
Определим опорные реакции в ферме. Горизонтальная нагрузка на систему отстутствует, следовательно горизонтальная реакция в левой опоре равна нулю  . Поскольку данная ферма симметрична и находится под действием симметричной нагрузки, очевидно, вертикальные реакции
. Поскольку данная ферма симметрична и находится под действием симметричной нагрузки, очевидно, вертикальные реакции  и
и  должны быть равными. Найдем их из уравнения проекций всех действующих на систему сил на вертикальную ось:
должны быть равными. Найдем их из уравнения проекций всех действующих на систему сил на вертикальную ось:  . Следовательно,
. Следовательно,  .
.
Теперь приступим к определению усилий в стержнях фермы. Прежде всего выделим нулевые стержни. Из рассмотрения узла 5 на основании признака 2 нулевых стержней следует, что стержень 5-6 нулевой.
Мысленно рассечем ферму сечением, изображенным на рис.32 и рассмотрим равновесие левой части. Напомним, что положительное значение продольного усилия соответствует растяжению стержня, а отрицательное - сжатию. Поэтому при составлении уравнений равновесия будем считать неизвестные стержневые усилия растягивающими.
|
Рис. 32 |
Из уравнения моментов относительно точки А  находим
находим  , а из уравнения моментов относительно точки В (ее положение легко определяется из подобия треугольников А43 и АВС)
, а из уравнения моментов относительно точки В (ее положение легко определяется из подобия треугольников А43 и АВС)  находим N3-6=60КН.
находим N3-6=60КН.
Усилие N4-6 можно определить из уравнения проекций всех сил на вертикальную ось  . Угол
. Угол  можно определить, например, из треугольника АВС:
можно определить, например, из треугольника АВС:  . Следовательно,
. Следовательно,  .
.
Усилия в остальных стержнях левой половины фермы можно найти, например вырезанием узлов 2, 3 и 4.
|
Рис. 33 |
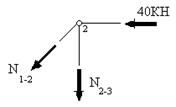
Рассотрим равновесие узла 2 (рис.33). Он соединяет три стержня, но в одном из них усилие уже найдено - усилие в стержне 2-5 является сжимающим и равно 40КН. Следовательно, двух уравнений равновесия этого узла будет достаточно, чтобы определить усилия в двух других стержнях. Из треугольника 123 следует, что  . Составим уравнения проекций сил на горизонтальную и вертикальную оси:
. Составим уравнения проекций сил на горизонтальную и вертикальную оси:  и
и  . Сопоставляя эти два уравнения, учитывая, что
. Сопоставляя эти два уравнения, учитывая, что  , получим:
, получим:  и
и  .
.
|
Рис. 34 |
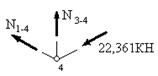
Рассмотрим равновесие узла 4 (рис.34). Он также соединяет три стержня, но в одном из них усилие уже найдено - усилие в стержне 4-6 является сжимающим и равно 22,361КН. Следовательно, двух уравнений равновесия этого узла будет достаточно, чтобы определить усилия в двух других стержнях. Из уравнения проекций сил на горизонтальную ось  следует:
следует:  . Из уравнения проекций сил на вертикальную ось
. Из уравнения проекций сил на вертикальную ось  следует:
следует: 
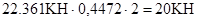
|
Рис. 35 |
Теперь рассмотрим равновесие узла 3 (рис.35). Усилия в трех стержнях из четырех, соединяющихся в этом узле, уже известны. Из уравнения проекций всех сил на горизонтальную ось находим  . Запишем уравнение проекций сил на вертикальную ось:
. Запишем уравнение проекций сил на вертикальную ось:  . Полученное равенство является истинным, что подтверждает правильность полученных значений усилий в стержнях ферм.
. Полученное равенство является истинным, что подтверждает правильность полученных значений усилий в стержнях ферм.
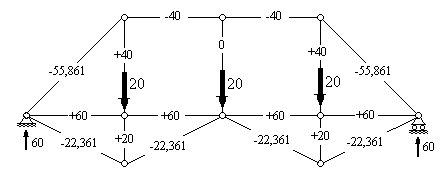
Итак, значения усилий в стержнях левой половины фермы определены. Усилия в стержнях на правой половине фермы находятся исходя из симметрии фермы и симметричности приложенной к ней нагрузки. Значения усилий (КН), определенные в результате расчета, приводятся на рис.36.
|
Рис. 36 |
Проверки правильности определения усилий в стержнях фермы также можно осуществить вырезанием узлов или использованием способа сечений.
Сопоставление балочных ферм различных типов.
Перед проектировщиком может встать задача выбора фермы наиболее рациональной конструкции. Под наиболее рациональной понимается такая конструкция, при которой усилия в стержнях фермы оказываются минимальными, что позволяет уменьшить расход материала, а значит и ее собственный вес. Кроме того, необходимо принимать во внимание вопросы, связанные с технологией изготовления, транспортировки и монтажа конструкций ферм.
Рассмотрим четыре фермы, перекрывающие один и тот же пролет -30м, имеющие одинаковую высоту в середине пролета - 5м, характеризующиеся одним и тем же числом панелей- 6 и находящиеся под действием одной и той же нагрузки - ко всем узлам верхнего пояса приложены напрвленные вертикально вниз силы величиной 10КН, а ко всем узлам нижнего пояса - 30КН.
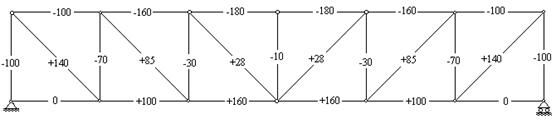
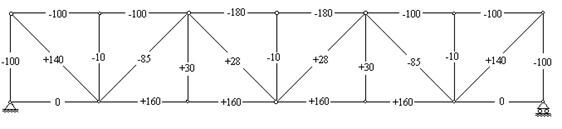
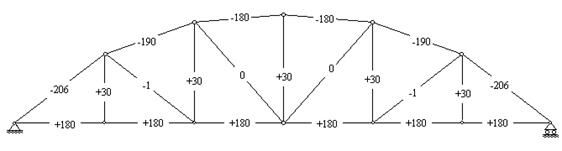
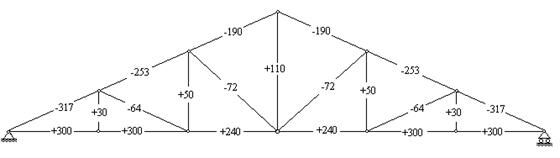
Первая ферма - с параллельными поясами и нисходящими раскосами (рис.37), вторая - с параллельными поясами и треугольной решеткой с дополнительными вертикальными стойками (рис.38), третья - с параболическим очертанием верхнего пояса и нисходящими раскосами (рис.39), четвертая - треугольная стропильная ферма с нисходящими раскосами (рис.40). На рисунках приводятся значения усилий (КН) в стержнях ферм, полученные в результате их статического расчета[2].
|
Рис. 37 |
|
Рис. 38 |
|
Рис. 39 |
|
Рис. 40 |
Как и следовало ожидать, стержни верхнего пояса во всех четырех случаях оказались сжатыми, а нижнего - растянутыми.
В балочных фермах с параллельными поясами в стержнях верхнего и нижнего поясов усилия увеличиваются от опор к центру пролета. Поэтому, если стержни верхнего и нижнего поясов выполняются постоянного по длине пролета сечения, то материал стержней поясов вблизи опор используется нерационально. Изготовление же стержней поясов фермы переменного по длине фермы сечения обычно является нерациональным из технологических соображений. Поэтому фермы с параллельными поясами не используют при очень больших пролетах и нагрузках, когда задача экономии материала и облегчения конструкции фермы приобретает особую важность.
Нисходящие раскосы в фермах с параллельными поясами работают на растяжение, восходящие - на сжатие, причем замена раскоса с нисходящего на восходящий приводит к изменинению знака усилия в нем, но абсолютная величина усилия остается постоянной.
Балочные фермы с параболическим очертанием верхнего пояса лишены основного недостатка ферм с параллельными поясами. Усилия в стержнях нижнего пояса постоянны по длине пролета, а верхнего пояса - меняются незначительно. Раскосы в такой ферме вообще практически не работают. То есть ферма этого типа представляется наиболее выгодной с точки зрения напряженного состояния. В то же время технология такой фермы несколько сложнее. Поэтому фермы с параболическим или близким к нему, трапецеидальным очертанием верхнего пояса используют для перекрытия весьма больших пролетов и при действии достаточно высокой нагрузки.
В треугольной ферме величины усилий в стержнях заметно выше, чем в фермах других типов. Усилия в верхнем и нижнем поясах распределены крайне неравномерно по длине пролета, увеличиваясь от середины пролета к опорам. Таким образом, треугольные фермы являются наименее выгодными по сравнению с фермами других типов. Их имеет смысл использовать там, где применение ферм других типов нерационально по конструктивным соображениям, например, в качестве стропильных ферм в двускатных зданиях небольшой ширины.
Расчет ферм на подвижную нагрузку.
Подвижной нагрузкой будем называть такую, как правило, вертикальную нагрузку, которая может перемещаться в пределах сооружения. Подобная нагрузка создается, например, движущимся по мосту транспортом или перемещающимися по подкрановым путям мостовыми кранами. При этом усилия, возникающие в сооружении, будут зависеть от положения нагрузки. Будем считать, что нагрузка перемещается по сооружению с небольшими ускорениями, поэтому динамическими эффектами, возникающими при этом можно пренебречь.
Задача расчета сооружений на подвижную нагрузку состоит в определении внутренних усилий в ее сечениях при любом ее положении. В частности, важно найти невыгоднейшее или опасное положение нагрузки, т.е. такое положение, при котором усилие в данном элементе конструкции достигает максимального по модулю значения. По усилиям, возникающим при невыгоднейшем положении груза, и выполняется подбор сечения стержней в системе.
Поскольку фермы часто используются в пролетных строениях мостов, в качестве несущих конструкций эскалаторов в метрополитенах, как стрелы подъемных кранов, их часто приходится расcчитывать на действие подвижной нагрузки.
Расчет стержневых систем на подвижную нагрузку выполняется при помощи линий влияния. Линия влияния внутреннего усилия в каком -либо сечении стержня - график зависимости этого усилия от положения единичной вертикальной силы на ездовой линии.
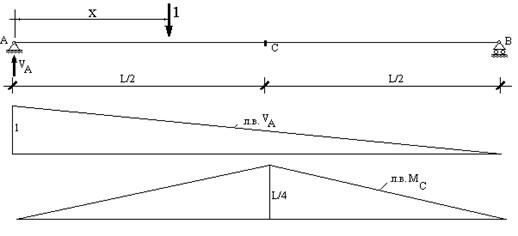
Рассмотрим вначале простую балку на двух опорах, перекрывающую пролет L (рис.41). Построим линии влияния реакции в левой опоре  и изгибающего момента
и изгибающего момента  в сечении в центре балки.
в сечении в центре балки.
Пусть единичная сила приложена на расстоянии х от левой опоры. Из условия равенства нулю суммы проекций всех действующих на систему сил на вертикальную ось имеем  . Из условия равенства нулю суммы всех приложенных к системе моментов относительно точки А имеем
. Из условия равенства нулю суммы всех приложенных к системе моментов относительно точки А имеем  . Отсюда следует, что
. Отсюда следует, что  . График данной зависимости и представляет собой линию влияния опорной реакции
. График данной зависимости и представляет собой линию влияния опорной реакции  (рис.41). При построении линий влияния ее положительные ординаты принято откладывать вверх.
(рис.41). При построении линий влияния ее положительные ординаты принято откладывать вверх.
|
Рис. 41 |
Итак, при перемещении груза от левой опоры к правой величина опорной реакции  уменьшается от единицы до нуля по линейному закону.
уменьшается от единицы до нуля по линейному закону.
Для построения линии влияния изгибающего момента  необходимо рассмотреть два случая, когда груз находится левее и правее рассматриваемого сечения С. В первом случае (
необходимо рассмотреть два случая, когда груз находится левее и правее рассматриваемого сечения С. В первом случае ( ) выражение для изгибающего момента имеет вид
) выражение для изгибающего момента имеет вид 
 . Во втором случае
. Во втором случае 
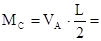
 . Соответственно, линия влияния
. Соответственно, линия влияния  состоит из двух ветвей (рис.41). Изгибающий момент в центре пролета балки равен нулю при нахождении груза на опорах и достигает максимального значения, когда положение единичной силы совпадает с рассматриваемым сечением (при
состоит из двух ветвей (рис.41). Изгибающий момент в центре пролета балки равен нулю при нахождении груза на опорах и достигает максимального значения, когда положение единичной силы совпадает с рассматриваемым сечением (при 
 ).
).
Важно четко уяснить разницу между эпюрой и линией влияния. При построении эпюры определяются внутренние усилия в различных сечениях системы при неподвижной нагрузке, а при построении линии влияния определяется усилие в каком-то одном сечении при разных положениях единичной силы, действующей на систему.
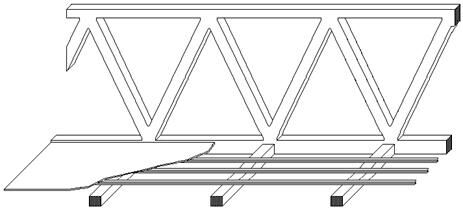
В фермах нагрузка обычно передается на узлы посредством вспомогательных конструкций, например через настил и систему продольных и поперечных балок (рис.42). То есть, если единичная сила находится на ездовой линии и не над узлом фермы, то все равно имеет место узловая передача нагрузки, а значит в стержнях фермы не возникает никаких усилий, кроме продольных.
|
Рис. 42 |
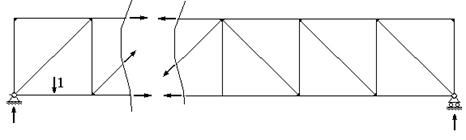
Для построения линий влияния в стержнях ферм применяют те же приемы, что и при определении усилий в них от действия неподвижной нагрузки, в частности способ сечений. Необходимо только задаться координатой единичной силы на ездовой линии и проанализировать зависимость величины усилия в стержне от ее изменения.
В некоторых фермах со сложной решеткой, например шпренгельных, линии влияния могут иметь довольно сложный вид.
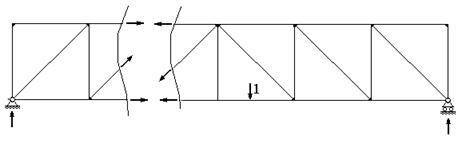
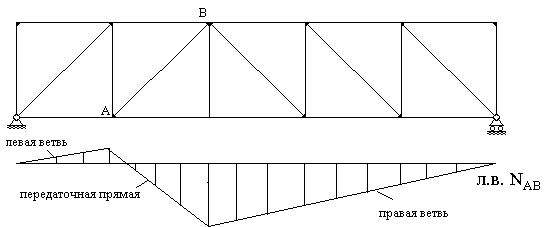
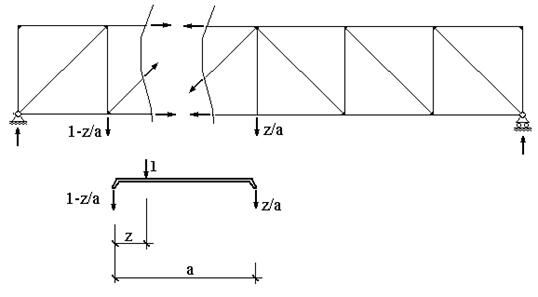
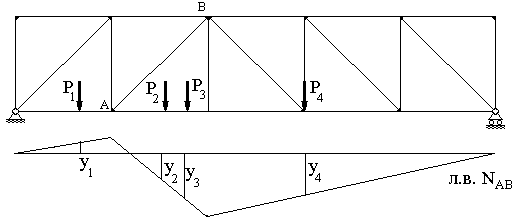
В раскосных фермах и фермах с треугольной решеткой ситуация несколько проще. Усилие в стержне при нахождении единичной силы слева от панели (рис.43), в которой находится этот стержень, будет меняться по одному закону, при нахождении справа от нее (рис.44) - по другому закону, а при нахождении в пределах данной панели (рис.45) - по третьему закону. В последнем случае необходимо учитывать, что часть от единичного усилия через вспомогательные конструкции передается на узел, лежащий на ездовой линии, слева от рассматриваемой панели, т.е. на часть фермы слева от сечения, а оставшаяся часть - на узел справа от рассматриваемой панели, т.е. с другой стороны от сечения. Таким образом, линии влияния продольного усилия в стержнях таких ферм в общем случае имеют три участка (рис.46), причем часть линии влияния в пределах панели, которой принадлежит данный стержень, носит название передаточной прямой.
|
Рис. 43 |
|
Рис. 44 |
После того, как для стержня построена линия влияния, с ее помощью можно решить следующие задачи.
|
Рис. 46 |
|
Рис.45 |
1. Пусть на ездовой линии находится груз величиной Р. Тогда усилие в стержне составит  , где y - ордината линии влияния под точкой приложения силы Р. Действительно, y -усилие, возникающее в стержне от действия приложенной в данной точке единичной силы. В силу линейности задачи, при увеличении нагрузки в Р раз, усилие в стержне тоже возрастет во столько-же раз.
, где y - ордината линии влияния под точкой приложения силы Р. Действительно, y -усилие, возникающее в стержне от действия приложенной в данной точке единичной силы. В силу линейности задачи, при увеличении нагрузки в Р раз, усилие в стержне тоже возрастет во столько-же раз.
На основании принципа независимости действия сил, если на ездовой линии имеется система из n сил, то усилие в стержне будет определяться по формуле:
|
| (3) |
где  - ордината линии влияния под i-ой силой величиной Pi (рис.47). Таким образом, линии влияния могут быть использованы и для определения усилий в стержнях ферм и при действии неподвижной нагрузки. Это может быть удобно, если нужно выполнить большое число расчетов для различных комбинаций нагрузок, приложенных к ферме.
- ордината линии влияния под i-ой силой величиной Pi (рис.47). Таким образом, линии влияния могут быть использованы и для определения усилий в стержнях ферм и при действии неподвижной нагрузки. Это может быть удобно, если нужно выполнить большое число расчетов для различных комбинаций нагрузок, приложенных к ферме.
|
Рис. 47 |
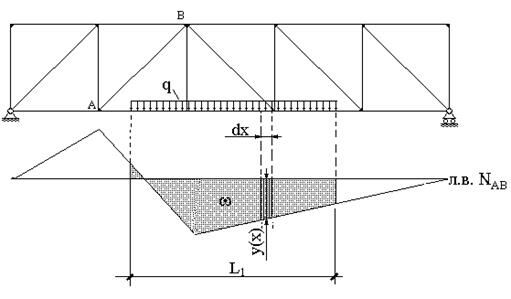
2. Пусть на участке длиной  ездовой линии действует равномерно распределенная нагрузка интенсивностью q. Во избежание недоразумений подчеркнем, что здесь как и ранее, так и далее, считается, что нагрузка приложена к вспомогательным конструкциям, а с них - передается на узлы фермы. В этом случае усилие в стержне фермы определяется по формуле:
ездовой линии действует равномерно распределенная нагрузка интенсивностью q. Во избежание недоразумений подчеркнем, что здесь как и ранее, так и далее, считается, что нагрузка приложена к вспомогательным конструкциям, а с них - передается на узлы фермы. В этом случае усилие в стержне фермы определяется по формуле:
|
| (4) |
где  - площадь, ограниченная линией влияния под зоной действия нагрузки q (рис.48). Действительно, выделим в зоне действия нагрузки q участок бесконечно малой длиной dx (рис.48). Элементарная равнодействующая сила, действующая на ферму, с этого участка составляет
- площадь, ограниченная линией влияния под зоной действия нагрузки q (рис.48). Действительно, выделим в зоне действия нагрузки q участок бесконечно малой длиной dx (рис.48). Элементарная равнодействующая сила, действующая на ферму, с этого участка составляет  , а усилие, возникающее от ее действия в стержне, в соответствии с формулой (3) составит
, а усилие, возникающее от ее действия в стержне, в соответствии с формулой (3) составит  .Для того, чтобы найти усилие в стержне от действия всей нагрузки, необходимо проинтегрировать dN по длине
.Для того, чтобы найти усилие в стержне от действия всей нагрузки, необходимо проинтегрировать dN по длине  :
: .
.
Очевидно, площадь в (4) необходимо определять с учетом знака. То есть, часть площади w снизу от горизонтальной оси учитывается со знаком “минус”.
|
Рис. 48 |
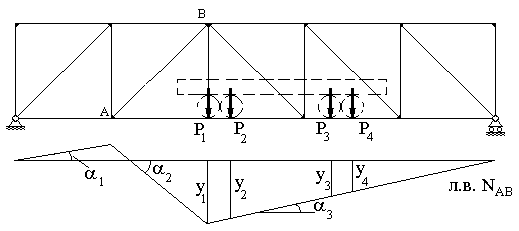
3. Пусть система грузов перемещается по ездовой линии, причем расстояния между грузами остаются постоянными. Такая ситуация имеет место, например, при движении поезда или мостового крана по пролетному строению моста или по подкрановым путям. Невыгоднейшее положение данной системы грузов возможно только при условии, что один из грузов находится над какой-либо вершиной линии влияния (рис.49). Подчеркнем, что это условие необходимое, но недостаточное. Иными словами, не при любом подобном положении нагрузки усилие в стержне имеет экстремальное значение.
|
Рис. 49 |
Например, для случая, приведенного на рис.49, усилие от системы грузов в соответствии с (3) составляет  . При сдвиге системы грузов вправо на величину
. При сдвиге системы грузов вправо на величину  такую, что ни одна из сил, приложенных к системе, не перейдет при этом через какую-либо вершину линии влияния и не выйдет за пределы фермы, усилие в стержне АВ составит:
такую, что ни одна из сил, приложенных к системе, не перейдет при этом через какую-либо вершину линии влияния и не выйдет за пределы фермы, усилие в стержне АВ составит:
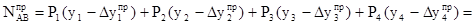
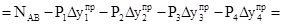
 .
.
При сдвиге влево на ту же величину  оно составит
оно составит 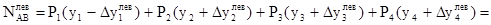
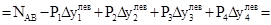
 .
.
Здесь  и
и  - абсолютные значения изменения ординаты линии влияния под i-м грузом при сдвиге системы грузов вправо и влево соответственно,
- абсолютные значения изменения ординаты линии влияния под i-м грузом при сдвиге системы грузов вправо и влево соответственно,  - абсолютное значение угла наклона линии влияния на i-м ее участке (рис.49).
- абсолютное значение угла наклона линии влияния на i-м ее участке (рис.49).
Таким образом, изменение величины усилия в стержне при сдвиге груза вправо составит  , а при сдвиге влево
, а при сдвиге влево  . Очевидно, эти значения могут быть как одного так и разных знаков. Если
. Очевидно, эти значения могут быть как одного так и разных знаков. Если  и
и  оказываются одного знака, то это значит, что при сдвиге системы грузов как вправо так и влево усилие в стержне либо уменьшается, либо увеличивается, то есть оно имеет локальный экстремум.
оказываются одного знака, то это значит, что при сдвиге системы грузов как вправо так и влево усилие в стержне либо уменьшается, либо увеличивается, то есть оно имеет локальный экстремум.
В то же время, для случая когда ни один из грузов не находится над вершиной линии влияния, величины и
и  могут быть только разных знаков, а значит эктремум усилия в стержне в этом случае невозможен.
могут быть только разных знаков, а значит эктремум усилия в стержне в этом случае невозможен.
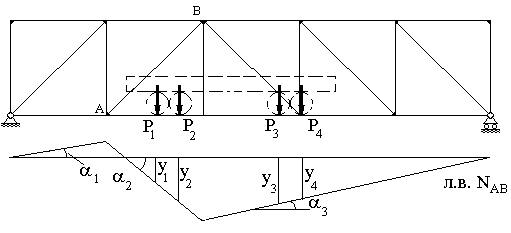
Действительно, рассмотрим в качестве примера ситуацию, изображенную на рис.50. В этом случае при сдвиге вправо:
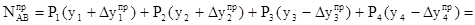
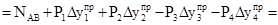
 ,
,  .
.
А при сдвиге влево:
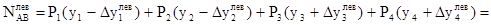
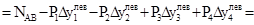
 ,
,  .
.
|
Рис. 50 |
Сопоставляя выражения для  и
и  , можно сделать вывод, что они не могут быть одного знака.
, можно сделать вывод, что они не могут быть одного знака.
Итак, для поиска максимально и минимально возможных усилий в стежнях фермы при действии на нее подвижной системы грузов достаточно рассматривать только такие положения этой системы, при которых хотя бы один из грузов находится над какой-либо вершиной линии влияния.
Пример расчета фермы на подвижную нагрузку.
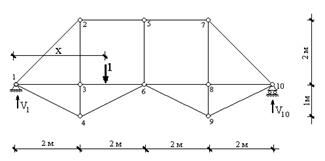
Рассмотрим ферму, изображенную на рис.31. Необходимо:
1. Используя теорию линий влияния, определить усилие в стержне фермы 2-3 от действия неподвижной системы сил, изображенной на рис.31.
2. Определить максимальное и минимальное усилия в стержне фермы 2-3 при движении по ездовой линии (по горизонтали от узла 1 к узлу 10) системы из двух сил (рис.51).
|
Рис. 51 |
3. Определить усилие от постоянной равномерно распределенной нагрузки q=10КН/м, приложенной к поясу фермы, совпадающему с ездовой линией (рис.52).
|
Рис. 52 |
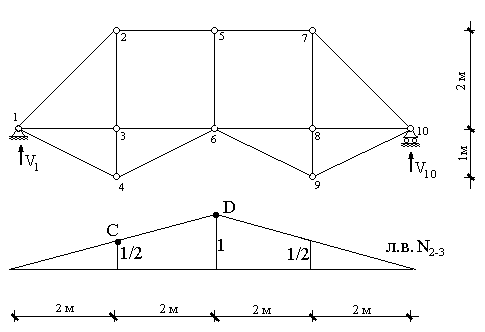
Построим линию влияния для стержня фермы 2-3[3]. Для этого достаточно определить усилие в этом стержне при различных положениях единичной силы на ездовой линии.
Если единичная сила находится на расстоянии х от левой опоры, то реакция в последней будет составлять  , а в правой опоре -
, а в правой опоре -  (рис.53).
(рис.53).
|
Рис. 53 |
|
Рис. 54 |
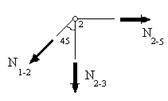
Cоставим уравнения равновесия узла 2 (рис.54):
 ,
,  , откуда следует, что
, откуда следует, что  . Поскольку , нагрузки к узлу 2 не приложены, т.к. он не лежит на ездовой линии, это уравнение справедливо при любом положении грузов на ней. Для определения
. Поскольку , нагрузки к узлу 2 не приложены, т.к. он не лежит на ездовой линии, это уравнение справедливо при любом положении грузов на ней. Для определения  воспользуемся способом сечений, причем рассмотрим два случая, когда единичный груз находится слева от панели, в которой располагается стержень 2-5 (рис.55), и справа от нее (рис.56).
воспользуемся способом сечений, причем рассмотрим два случая, когда единичный груз находится слева от панели, в которой располагается стержень 2-5 (рис.55), и справа от нее (рис.56).
|
Рис. 55 |
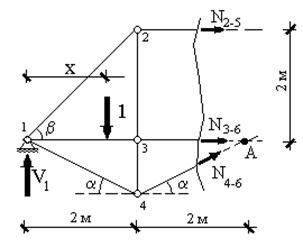
Для первого случая (рис.55) уравнения равновесия моментов относительно точки А примет вид:
|
Рис. 56 |
 , откуда:
, откуда:  . Следовательно, при нахождении единичного груза слева от рассеченной панели (x<2м)
. Следовательно, при нахождении единичного груза слева от рассеченной панели (x<2м)  , а
, а  .
.
Согласно этой формуле, при x=0 ордината линии влияния, как и следовало ожидать, равна нулю, а при x=2м она равна 1/2. По этим точкам строится левая ветвь линии влияния (до точки С на рис.57)
Для второго случая (рис.56) из аналогичных рассуждений получим:  , откуда:
, откуда:  . Следовательно, при нахождении единичного груза справа от рассеченной панели (x>4м)
. Следовательно, при нахождении единичного груза справа от рассеченной панели (x>4м)  , а
, а  . Таким образом, при x=4м ордината линии влияния равна 1 (точка D на рис.57), а на правой опоре, как и следовало ожидать -нулю. По этим точкам строится правая ветвь линии влияния, и далее передаточная прямая CD. В рассматриваемом случае ее направление, как мы видим, совпадает с направлением левой ветви линии влияния, а сама линия влияния оказалась симметричной.
. Таким образом, при x=4м ордината линии влияния равна 1 (точка D на рис.57), а на правой опоре, как и следовало ожидать -нулю. По этим точкам строится правая ветвь линии влияния, и далее передаточная прямая CD. В рассматриваемом случае ее направление, как мы видим, совпадает с направлением левой ветви линии влияния, а сама линия влияния оказалась симметричной.
Теперь приступим к определению усилий в стержне 2-3.
Для заданной неподвижной узловой нагрузки (рис.31) в соответствии с формулой (3) найдем величину усилия в стержне:  . Этот же ответ был получен нами ранее в разделе “Пример расчета фермы на неподвижную нагрузку” без использования линий влияния, что подтверждает правильность проделанных вычислений.
. Этот же ответ был получен нами ранее в разделе “Пример расчета фермы на неподвижную нагрузку” без использования линий влияния, что подтверждает правильность проделанных вычислений.
|
Рис. 57 |
|
Рис. 58 |
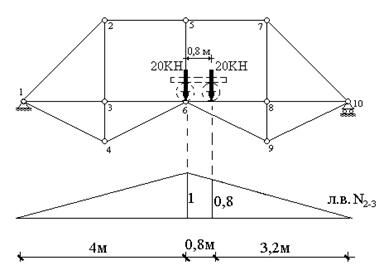
Наиневыгоднейшим положением подвижной системы двух сил на ездовой линии (рис.51) будет положение, когда одна из них находится ровно посередине пролета фермы (рис.58), т.к. в этом случае одна из сил оказывается над единственной в рассматриваемом случае вершиной линии влияния. Ордината линии влияния под силой в центре фермы равна 1, ординату под точкой приложения второй силы легко определить из подобия треугольников:  , откуда y=0,8 (рис.58). В соответствии с (3) усилие в стержне составит
, откуда y=0,8 (рис.58). В соответствии с (3) усилие в стержне составит  . В силу симметрии линии влияния, в случае, когда над ее вершиной в центре пролета фермы окажется не левая, а правая сила, результат будет тем же.
. В силу симметрии линии влияния, в случае, когда над ее вершиной в центре пролета фермы окажется не левая, а правая сила, результат будет тем же.
Построенная линия влияния не имеет отрицательных ординат, следовательно, при любом положении системы сил на ездовой линии в стержне будут возникать только растягивающие усилия. Поэтому, максимальным возможным усилием в стержне 2-3 для рассматриваемой подвижной нагрузки является 36КН, минимальным -0 КН.
Наконец, определим усилие в стержне от действия неподвижной равномерно распределенной по всей длине ездовой линии нагрузки (рис.52) q=10 КН/м. Площадь фигуры, ограниченной линией влияния (рис.57) составляет  . Размерность площади фигуры оказалась такой, поскольку единичная сила, а следовательно и ординаты линии влияния продольного усилия не имеют размерности.
. Размерность площади фигуры оказалась такой, поскольку единичная сила, а следовательно и ординаты линии влияния продольного усилия не имеют размерности.
Теперь, в соответствии с формулой (4), определим усилие в стержне:  .
.
Глоссарий
Висячие системы
Ездовая линия
Жесткий диск
Комбинированные системы
Линия влияния
Невыгоднейшее положение нагрузки
Нулевой стержень
Опасное положение нагрузки
Панель фермы
Передаточная прямая
Подвижная нагрузка
Пояс фермы верхний
Пояс фермы нижний
Проезжий пояс
Раскос
Раскос восходящий
Раскос нисходящий
Решетка фермы
Статический метод анализа геометрической неизменяемости ферм
Стойка
Структурный анализ фермы
Узлы фермы
Ферма
Ферма арочная
Ферма балочная
Ферма консольная
Ферма консольно-балочная
Ферма простейшая
Ферма раскосная
Ферма с треугольной решеткой
Лекция "Моделирование поведения потребителей" также может быть Вам полезна.
Ферма шпренгельная
Шарнирная схема
Шпренгель
[1] В.Г.Шухов (1853-1939) - выдающийся русский инженер, автор конструкций легких и экономичных перекрытий различных типов, высотной мачты первой радиотелеграфной станции в Москве (1921), известной как башня Шухова, автор многочисленных конструкторских решений в области добычи, переаботки, хранения и транспортировки нефти.
[2] Данные и результаты расчетов взяты из книги: Шишман Б.А. Статика сооружений: Учебник для техникумов.-М.:Стройиздат, 1989.-384с.”
[3] В состав настоящего учебника входит программа для ЭВМ “Построение линий влияния в фермах”, разаработанная кафедрой строительной механики и теории упругости СПбГТУ.

 Рис. 1
Рис. 1
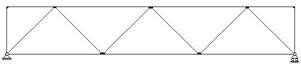
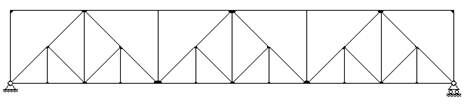
 Рис. 5
Рис. 5 Рис. 6
Рис. 6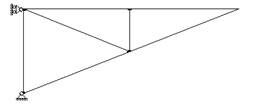

 ,
,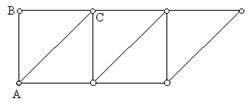
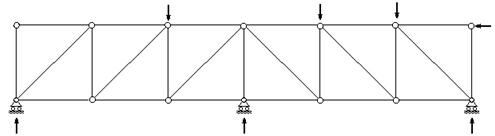
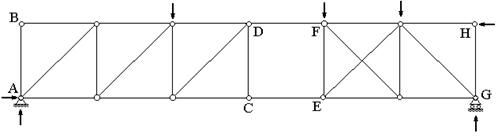
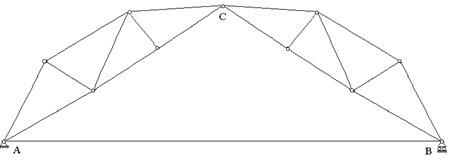
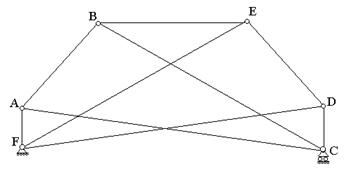
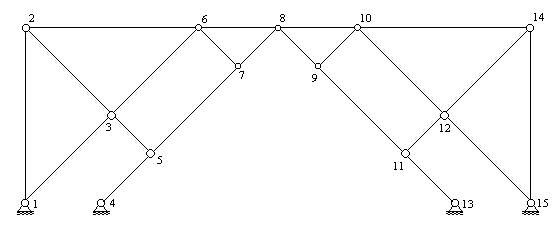
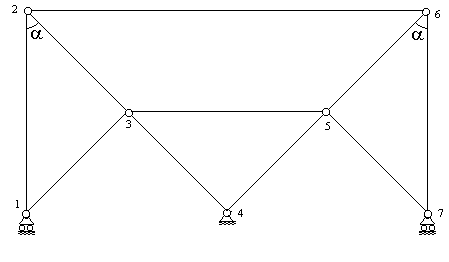
 Рис. 28
Рис. 28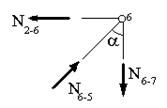
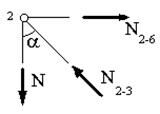
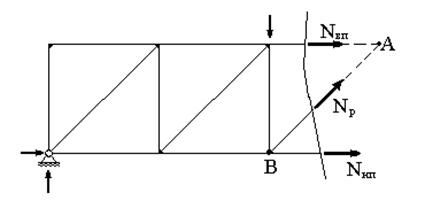
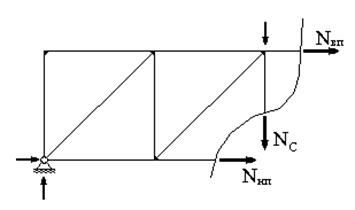
 Рис. 31
Рис. 31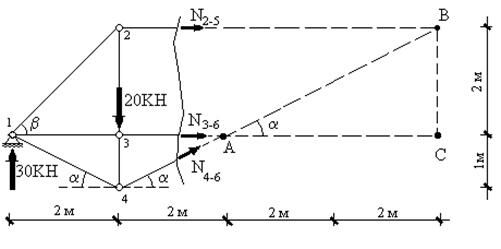
 ,
,
 ,
,