Дисперсия и поглощение света

Лекция № 11

Дисперсия и поглощение света

Исследования показали, что показатель преломления среды зависит от частоты или длины волны, т.е. n=f(ω). Эта зависимость и называется дисперсией света. Очень наглядный метод исследования дисперсии материала был применен Ньютоном. Это метод скрещенных призм. Пучок света проходит через две призмы установленные таким образом, чтобы преломляющие ребра их были расположены перпендикулярно друг другу. Цветная полоса, получающаяся после прохождения света одной призмы, отклоняется второй призмой. На экране получается окончательная форма, определяемая величиной дисперсии обеих призм. Зависимость между показателем преломления и частотой света может быть весьма сложной. Если показатель преломления увеличивается с увеличением частоты ω, то дисперсия называется нормальной, если зависимость имеет обратный характер, то дисперсия называется аномальной. Аномальную дисперсию наблюдать очень трудно, так как она обычно располагается в области поглощения света веществом.

Рождественский, используя интерферометр и спектрограф, предложил метод крюков, позволивший значительно повысить точность измерения дисперсии в непосредственной близости к полосе поглощения.

Объяснение явления дисперсии света удалось объяснить только после более глубокого рассмотрения взаимодействия световых волн с веществом.

Для вывода зависимости показателя преломления от частоты нужно найти как зависит диэлектрическая проницаемость от частоты (длины) переменного электрического поля. Дело в том, что показатель преломления связан с фазовой скоростью , а скорость определяется из электромагнитной теории Максвелла . Откуда . Для большинства прозрачных тел μ=1 и следовательно .

Будем рассматривать молекулы или атомы диэлектрика как систему,  в которую входят электроны, находящиеся в молекулах (атомах) в положении равновесия. Под влиянием внешнего поля эти заряды смещаются из положения равновесия на расстояние r, превращая атом в электрический диполь с моментом . Если в единице объема среды находится N атомов, то электрический момент единицы объема (поляризация) среды будет . Зная поляризацию среды можно вычислить ее диэлектрическую проницаемость ε, так как индукция . Следовательно

                                                  (1)

Таким образом, задача сводится к определению смещения электрона r под действием внешнего периодически меняющегося поля при учете сил действующих на электрон, входящий в состав атома, со стороны частей этого атома и окружающих атомов. 

Рекомендуемые материалы

В связи с этим, запишем уравнение движения электрона. Световую волну запишем в виде , следовательно, сила со стороны этого поля на электрон будет меняться таким же образом. На смещенный электрон со стороны атома будет действовать упругая сила, пропорциональная смещению, т.е. – . Кроме того, необходимо учесть и силу, приводящую к затуханию возникающих колебаний электрона (сила сопротивления), которая будет пропорциональна скорости электрона, т.е. – .

Таким образом, уравнение движения запишется следующим образом

                                                        (2)

Разделим на m и перенесем все слагаемые с  в левую сторону, получим

,

обозначим  и , тогда уравнение перепишется в виде

                                             (3)

Это уравнение колебания, собственная частота которого .

Собственные колебания такой связанной системы в твердом теле быстро затухают и остаются только вынужденные, которые происходят по закону вынуждающей силы. Поэтому решением этого уравнения будет . Подставляя значения смещения  в уравнение (3), получим

.                                        (4)

Подставляя его в выражение для n (1) получим

.                                  (5)

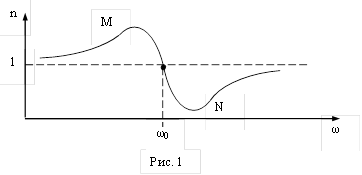
Таким образом, показатель преломления зависит от частоты ω внешнего поля. В области ω=0 до ω=ω₀ n>1 и возрастает при возрастании ω (нормальная дисперсия). От ω=ω₀ до ω= ∞ n<1 и также возрастает от -∞ до 1 (нормальная дисперсия).

График зависимости n(ω) представлен на рис. 1. В области ω₀ (MN) показатель преломления с увеличением частоты уменьшается. Это область аномальной дисперсии. Она связана с поглощением света.

Если учесть, что в веществе может быть несколько сортов заряженных частиц с массами m_i и собственными частотами ω_0i и зарядами е_i, то уравнение дисперсии запишется следующим образом

                                         (6)

Рассмотрим связь дисперсии и поглощения, т.е. показателя преломления n и коэффициента поглощения a.

Эмпирический закон поглощения Бугера имеет вид I=I₀e^-αl, где a – коэффициент поглощения. Комплексный показатель преломления связан с коэффициентом экстиниции æ, , волновой вектор . Падающая световая волна , а выходящая из вещества толщиной х будет

,                    (7)

где амплитудное значение  (8). Для интенсивности, следовательно,

                                                (9)

Сравнивая с эмпирическим законом, запишем выражение для коэффициента поглощения

                                                  (10)

Фазовая и групповая скорости света

Измерения скорости света Майкельсоном методом вращающегося зеркала в сероуглероде дали для отношения . Однако это же отношение, определенное по показателю преломления оказалось n=1,64. Объяснение этого различия дал Рэлей, предложивший ввести понятие двух скоростей света: фазовой и групповой.

Если записать световую волну в виде Е=Е₀sin(ωt-кх), то фазовую скорость найдем из условия постоянства фазы ωt-кх=const. Продифференцировав, найдем ωdt-кdх=0 или. Учитывая  и  получим , т.е. скорость фазы.

Естественный свет представляет собой сложный пакет цугов волн. В вакууме скорости для всех волн одинаковы и этот пакет имеет такую же скорость. В среде, обладающей дисперсией, световые волны распространяются с различными фазовыми скоростями, для каждой волны – своя. Пакет деформируется, и, если мы следим за максимумом амплитуды, то его скорость уже не будет совпадать с фазовыми скоростями волн, образующих этот пакет. Для простоты рассмотрения будем представлять пакет, состоящий из двух близких по частоте синусоид одинаковой амплитуды (рис. 2). 

Наложение таких близких синусоид дает импульс, форма которого представляет биение близких по частоте колебаний.

Запишем эти волны Е₁=Е₀sin(ω₁t-к₁х) и Е₂=Е₀sin(ω₂t-к₂х). Считаем, что

ω₁=ω₀+δω и ω₂=ω₀-δω                                      (10)

  к₁=к₀+δк и к₂=к₀-δк

Запишем суммарный импульс

Е=Е₁+Е₂=Е₀sin(ω₁t-к₁х)+Е₀sin(ω₂t-к₂х)=

==

=2Е₀cos(tδω-хδк)sin(ω₀t-к₀х).

Выражение 2Е₀cos(tδω-хδк)=А является амплитудой импульса. Тогда импульс запишется в виде Е=А sin(ω₀t-к₀х). Здесь А не является постоянной, а меняется во времени и в пространстве однако меняется медленно, т.к. dω и dк малы по сравнению c ω₀ и к₀. Выбираем А – максимальную и определим ее скорость, которая называется групповой. Это скорость переноса энергии. Запишем условие постоянства амплитуды t·δω-xδк=const. Дифференцируя, находим

δωd t-δxdx=0 или                                    (11)

Найдем связь между скоростями u и υ. . Учитывая,; ;  тогда

 – формула Рэлея                        (12)

Если  (нормальная дисперсия), то u<υ, если  (аномальная дисперсия), то u>υ. При отсутствии дисперсии , u=υ.

Рассеяние света

Вторичные волны, вызываемые вынужденными колебаниями электронов, рассеивают в стороны часть энергии переносимой световой волной. Поэтому распространение света в веществе должно сопровождаться рассеянием света. Однако, как правило, мы чаще всего не наблюдаем этого. Это объясняется тем, что вторичные волны когерентны между собой и взаимно интерферирует. Поэтому волны, идущие в стороны, в значительной степени или полностью компенсируют друг друга.

Опыт показывает, что необходимым условием явление рассеяния света является нарушение однородности среды. Выясним, что необходимо для однородности среды. Оптическая однородность определяется постоянством показателя преломления n, который связан с диэлектрической проницаемостью среды , а εE=E+4πP, поляризация среды P=Np , где N – число молекул в единице объема. Электрический момент молекулы p=кЕ, где к – коэффициент поляризации. Следовательно, P=NкE , D=εE=E+4πNкE или

ε=1+4πNк.                                                        (12)

Таким образом, постоянство показателя преломления определяется произведением Nк. Среда будет неоднородной, если она представлена из разных молекул (разные к) или при равных к, но разная плотность N. Если неодинаковое к, то рассеивающие среды называются мутными средами.

Исследование рассеяния в мутных средах, когда размеры частиц сравнимы с длиной волны, привело к установлению некоторых закономерностей.

1) Интенсивность рассеянного света зависит от длины волны

 – закон Рэлея.

2) Рассеянный свет поляризован. Направление электрического вектора перпендикулярно плоскости, проходящей через направление первичного пучка и направления наблюдения.

3) Индикатриса рассеяния выражается в виде I_φ=I_π/2(1+cos²φ). φ – угол направления наблюдателя.

При одном к, но разном по объему N имеет место молекулярное рассеяние. Это рассеяние обусловлено флуктуациями плотности. Интенсивность молекулярного рассеяния возрастает с повышением температуры. Молекулярным рассеянием объясняется голубой цвет неба.

Комбинационное рассеяние света

Тщательное изучение показало, что в спектре рассеянного света наблюдаются кроме линий, характеризующих падающий свет, еще добавочные линии – спутники, сопровождающие каждую из линий первичного света. При этом необходимо, чтобы первичный спектр был линейчатым. Опыты показали, что:

Бесплатная лекция: "2.1 Однокристалльные микропроцессоры" также доступна.

1) Спутники сопровождают каждую линию первичного света.

2) Различие Δν в частотах возбуждающей первичной линии ν₀ и линии каждого из спутников характерно для рассеивающего вещества и равно частотам собственных инфракрасных колебаний νⁱ его молекул. Δν₁=ν₀–ν'=ν₁ⁱ, Δν₂=ν₀–ν''=ν₂ⁱ; Δν₃=ν₀–ν'''=ν₃ⁱ.

3) Спутники представляют собой две системы линий, лежащих симметрично по обе стороны от возбуждающей линии, т.е. ν₀–ν_кр=ν_ф–ν₀ (красные и фиолетовые спутники).

С повышением температуры интенсивность «фиолетовых» спутников возрастает.

Объяснение комбинационного рассеяния находит в квантовой теории света.

Если падающий свет имеет частоту ν₀, то квант энергии hν₀ света при столкновении с молекулами, обладающими частотой колебаний ν_i, могут ими частично поглотиться hν'=hν₀–hν_i; ν'=ν₀–ν_i или отобрать от молекулы энергию hν_i, т.е. hν'=hν₀+hν_i; ν'=ν₀–ν_i, т.е. возникают или красные или «фиолетовые» спутники. С повышением температуры, увеличивается число возбужденных молекул и, при этом, будет возрастать интенсивность «фиолетовых» спутников.