Геометрические характеристики плоских сечений
1.2 Геометрические характеристики плоских сечений
Геометрические характеристики – числовые величины (параметры), определяющие размеры, форму, расположение поперечного сечения однородного по упругим свойствам деформируемого элемента конструкции (и, как следствие,
характеризующие сопротивление элемента различным видам деформации).
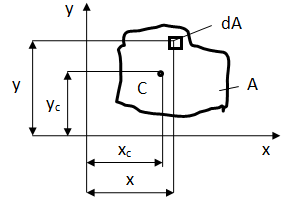
Площадь поперечного сечения

 - площадь поперечного сечения. Размерность м2.
- площадь поперечного сечения. Размерность м2.
Статические моменты
 - статический момент относительно оси х,
- статический момент относительно оси х,
 - статический момент относительно оси y.
- статический момент относительно оси y.
Рекомендуемые материалы
Статический момент относительно данной оси – сумма произведений элементарных площадей dA на их расстояние до данной оси, взятая по всей площади сечения А.
На основании теоремы Вариньяна (из курса теоретической механики) следует, что
 ,
,  , (1.4)
, (1.4)
а для сложного сечения (состоящего из нескольких простых, каждое из которых имеет площадь Аi и координаты собственного центра тяжести yci , xci)
 ,
,  . (1.5)
. (1.5)
Статический момент относительно какой-либо оси равен произведению всей площади фигуры на расстояние от ее центра тяжести до этой оси.
Размерность статических моментов площади м3. Статические моменты площади могут быть положительны, отрицательны и равные нулю. Оси, относительно которых статические моменты площади равны нулю, называются центральными осями (это две взаимноперпендику-лярные оси, проходящие через центр тяжести поперечного сечения).
Осевые моменты инерции
 - осевой момент инерции относительно оси х,
- осевой момент инерции относительно оси х,
 - осевой момент инерции относительно оси y.
- осевой момент инерции относительно оси y.
Осевой момент инерции относительно рассматриваемой оси – сумма произведений элементарных площадей dA на квадрат их расстояний до этой оси, взятая по всей площади сечения А.
Осевые моменты инерции имеют размерность м4 и всегда положительны
Центробежный момент инерции
 - центробежный момент инерции.
- центробежный момент инерции.
Центробежный момент инерции относительно осей координат – сумма произведений элементарных площадей dA на их расстояния до этих осей, взятая по всей площади сечения А.
Центробежный момент инерции имеют размерность м4 и может быть положительным, отрицательным и равным нулю. Оси, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями.
Главные центральные оси – это оси, осевые моменты инерции относительно которых принимают свои экстремальные значения (максимум и минимум).
Полярный момент инерции
 (1.6)
(1.6)
 . (1.7)
. (1.7)
Полярный момент инерции относительно данной точки – сумма произведений элементарных площадей dA на квадраты их расстояний ( ) до этой точки, взятая по всей площади сечения А.
) до этой точки, взятая по всей площади сечения А.
Моменты сопротивления
Осевой момент сопротивления относительно рассматриваемой оси – величина равная моменту инерции относительно той же оси отнесенному к расстоянию до наиболее удаленной от этой оси точки
 ;
;  . (1.8)
. (1.8)
Полярный момент сопротивления
 (1.9)
(1.9)
Осевой и полярный моменты инерции имеют размерность м3.
Радиус инерции
Радиусом инерции сечения относительно некоторой оси, называется величина, определяемая из соотношения:
 ;
;  . (1.10)
. (1.10)
Вычисление геометрических характеристик простых фигур
Прямоугольное сечение.
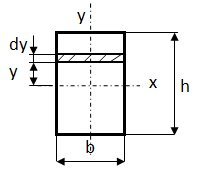
Определим осевой момент инерции прямоугольника относительно оси х.
 Разобьем площадь прямоугольника на элементарные площадки с размерами b (ширина) и dy (высота). Тогда площадь такого элементарного прямоугольника (заштрихована) равна
Разобьем площадь прямоугольника на элементарные площадки с размерами b (ширина) и dy (высота). Тогда площадь такого элементарного прямоугольника (заштрихована) равна  . Подставляя значение dA в формулу для определения осевого момента инерции, получим:
. Подставляя значение dA в формулу для определения осевого момента инерции, получим:
 (1.11)
(1.11)
По аналогии запишем
 . (1.12)
. (1.12)
Рекомендация для Вас - Выбор экономического критерия.
Круглое сечение
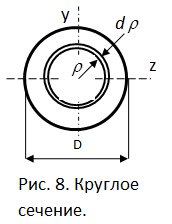
Сначала удобно найти полярный момент инерции. Затем, учитывая, что для круга  , а
, а  , найдем
, найдем  .
.
Разобьем круг на бесконечно малые кольца толщиной d и радиусом
и радиусом  ; площадь такого кольца
; площадь такого кольца  . Подставляя выражение для площади кольца в выражение для
. Подставляя выражение для площади кольца в выражение для  и интегрируя, получим:
и интегрируя, получим:  Тогда
Тогда
 (1.13)
(1.13)





















