Индуктивный элемент в цепи синусоидального тока

2.6. Индуктивный элемент в цепи синусоидального тока.

Индуктивный элемент учитывает явления накапливания энергии магнитного поля и характеризуется зависимостью потокосцепления  от тока i:

, измеряется в генри (Гн).

2.6.1. Мгновенное значение напряжения на индуктивности:

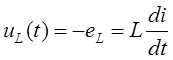
Здесь  - ЭДС, наводимая изменяющимся во времени магнитным потоком.

Если принять ток в катушке , то напряжение запишется в виде:

.

Рекомендуемые материалы

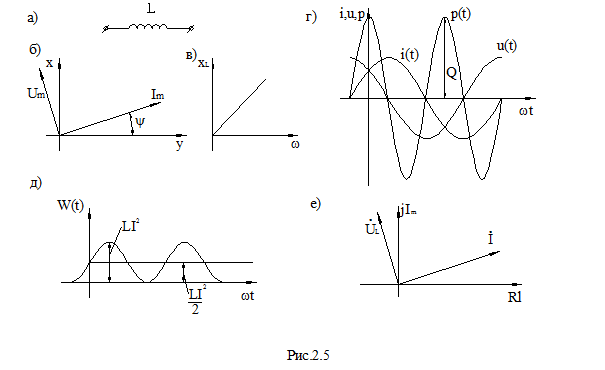
Векторы тока и напряжения показаны на рис. 2.5б. Напряжение опережает ток в катушке на угол . Закон Ома для индуктивности:

          или             ,

где  - индуктивное сопротивление катушки, измеряется в Омах (Ом). Сопротивление  - частично зависимая величина, увеличивается с ростом частоты, рис. 2.5в.

2.6.2. Мгновенная мощность:

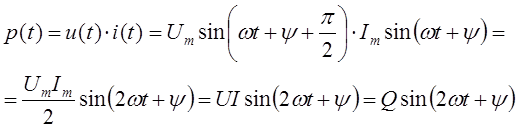
Мощность  называется реактивной и измеряется в вольт-амперах реактивных (ВАр). Временные диаграммы w(t), i(t) и p(t) для катушки приведены на рис. 2.5г. Средняя мощность равна нулю, т.е. рассеивание мощности или потери отсутствуют. Энергия магнитного поля катушки равна:

Временная диаграмма W(t), приведена на рис. 2.5д. Максимальная энергия магнитного поля катушки:

.

2.6.3. Напряжение на индуктивности в комплексной форме.

Так как напряжение на катушке:

,

Инвестиционный менеджмент и риск - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

то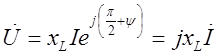     

Здесь  - индуктивное сопротивление в комплексной форме.

Оператор  отражает дифференцирование напряжения на индуктивности.

Закон Ома в комплексной форме:

              или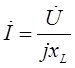            

Вектора тока и напряжения на комплексной плоскости приведены на рис. 2.5е.