Магнитный и механический момент электрона
§ 5.3. Магнитный и механический момент электрона.
Движение электрона вокруг ядра эквивалентно круговому току. Магнитный момент тока определяется по известной формуле:  , где
, где  – ток, протекающий по контуру, а
– ток, протекающий по контуру, а  – площадь контура. В случае электрона
– площадь контура. В случае электрона  , где
, где  – заряд электрона, а
– заряд электрона, а  – период его обращения вокруг ядра. Таким образом,
– период его обращения вокруг ядра. Таким образом,  , здесь
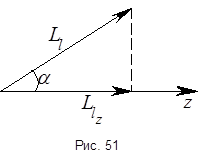
, здесь  – площадь, охватываемая орбитой электрона. Как уже было сказано выше, электрон движется в поле центральных сил. В поле центральных сил момент импульса является интегралом движения1. Поэтому в полярной системе координат:
– площадь, охватываемая орбитой электрона. Как уже было сказано выше, электрон движется в поле центральных сил. В поле центральных сил момент импульса является интегралом движения1. Поэтому в полярной системе координат:  . Пусть начало координат совпадает с ядром. Площадь орбиты электрона есть:
. Пусть начало координат совпадает с ядром. Площадь орбиты электрона есть:  . Из предыдущей формулы найдём
. Из предыдущей формулы найдём  :
:  . Тогда:
. Тогда:  ;
;  . Тогда магнитный момент электрона:
. Тогда магнитный момент электрона:  ,
,  . Для положительно заряженной частицы вектора
. Для положительно заряженной частицы вектора  и
и  коллинеарны. В общем же случае:
коллинеарны. В общем же случае:  . Применительно же к электрону,
. Применительно же к электрону,  ,
,  . Таким образом, мы получили связь между магнитным и механическим моментом электрона. Совершим некоторые преобразования. Умножим последнюю формулу на дробь
. Таким образом, мы получили связь между магнитным и механическим моментом электрона. Совершим некоторые преобразования. Умножим последнюю формулу на дробь  . Получим:
. Получим:  . Введём следующее обозначение:
. Введём следующее обозначение:  . Величину
. Величину  называют магнетоном Бора. Тогда последняя формула перепишется так:
называют магнетоном Бора. Тогда последняя формула перепишется так:  . В системе СИ
. В системе СИ  . По аналогии квантово-механический магнитный момент связан с квантово-механическим орбитальным моментом таким же соотношением:
. По аналогии квантово-механический магнитный момент связан с квантово-механическим орбитальным моментом таким же соотношением:  . Найдём выражение для проекции магнитного
. Найдём выражение для проекции магнитного
момента на какую-либо ось, например, на ось  :
:  , где
, где  – проекция орбитального момента на заданное направление. Так как
– проекция орбитального момента на заданное направление. Так как  может принимать только
может принимать только  значение:
значение:  , то существует
, то существует  способа ориентации магнитного момента. Так как в сферически симметричной системе координат в качестве оси
способа ориентации магнитного момента. Так как в сферически симметричной системе координат в качестве оси  можно выбрать любую, то и полученное соотношение будет справедливо для проекции магнитного момента на любую ось.
можно выбрать любую, то и полученное соотношение будет справедливо для проекции магнитного момента на любую ось.
Рассмотрим углы, которые образует орбитальный момент с осью  .
.  . Максимальное значение, которое может принимать орбитальное квантовое число –
. Максимальное значение, которое может принимать орбитальное квантовое число –  , поэтому
, поэтому  , так как
, так как  – величина положительная. Таким образом, квантово-механический орбитальный момент никогда не может быть сонаправленым с осью, относительно которой он рассматривается. Вообще говоря, он не может быть ориентирован строго по какой-либо определённой оси. Причём
– величина положительная. Таким образом, квантово-механический орбитальный момент никогда не может быть сонаправленым с осью, относительно которой он рассматривается. Вообще говоря, он не может быть ориентирован строго по какой-либо определённой оси. Причём  может принимать только различные дискретные значения, в зависимости от
может принимать только различные дискретные значения, в зависимости от  . Эта дискретность в ориентации момента импульса называется пространственным квантованием.
. Эта дискретность в ориентации момента импульса называется пространственным квантованием.
Отношение  модуля магнитного момента к модулю механического момента, выраженное в единицах
модуля магнитного момента к модулю механического момента, выраженное в единицах  , называется гиромагнитным отношением:
, называется гиромагнитным отношением:  . Очевидно, что для орбитального и магнитного и механического моментов электрона гиромагнитное соотношение равно единице, т. е.
. Очевидно, что для орбитального и магнитного и механического моментов электрона гиромагнитное соотношение равно единице, т. е.  . Для собственного магнитного момента электрона, обусловленного наличием спина:
. Для собственного магнитного момента электрона, обусловленного наличием спина:  . Тогда гиромагнитное отношение для спинового магнитного момента и механического момента
. Тогда гиромагнитное отношение для спинового магнитного момента и механического момента  .
.
Итак, электрон обладает в атоме четырьмя моментами:
1. Механическим (орбитальным и спиновым);
2. Магнитным (орбитальным и спиновым).
Рекомендуемые материалы
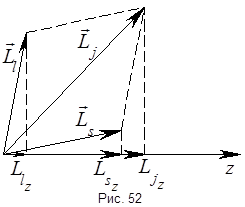
Полный механический момент импульса электрона является векторной суммой орбитального механического момента и спинового механического момента:  . Так как модули каждого момента всегда квантуются:
. Так как модули каждого момента всегда квантуются:  ,
,  то и их сумма должна квантоваться:
то и их сумма должна квантоваться:  , где
, где  – квантовое число полного механического момента электрона. Найдём его. Рассмотрим значения проекций на ось
– квантовое число полного механического момента электрона. Найдём его. Рассмотрим значения проекций на ось  :
:  –
–  значение;
значение;  . Тогда
. Тогда  ;
;  , где
, где  –
–  значение. Так как
значение. Так как  ,
,
В лекции "Наблюдение сущность и порядок проведения" также много полезной информации.
то тогда  . Определим угол между орбитальным и спиновым моментами электрона. Так как
. Определим угол между орбитальным и спиновым моментами электрона. Так как  , то, возводя это выражение в квадрат, получим:
, то, возводя это выражение в квадрат, получим:  . Отсюда
. Отсюда  , или
, или  . Так как возможно лишь
. Так как возможно лишь  – 2 состояния, то существует 2 возможных угла между орбитальным и спиновым моментами. Так как направление момента относительно любой оси не определено, то возникает вопрос, что же понимать под углом между этими моментами? Смысл данного угла в том, что в отсутствии внешних сил полный момент импульса сохраняется, орбитальный и спиновой моменты прецессируют вокруг полного момента, а их проекции на направление полного момента имеют вполне определённые значения (рис. 53).
– 2 состояния, то существует 2 возможных угла между орбитальным и спиновым моментами. Так как направление момента относительно любой оси не определено, то возникает вопрос, что же понимать под углом между этими моментами? Смысл данного угла в том, что в отсутствии внешних сил полный момент импульса сохраняется, орбитальный и спиновой моменты прецессируют вокруг полного момента, а их проекции на направление полного момента имеют вполне определённые значения (рис. 53).
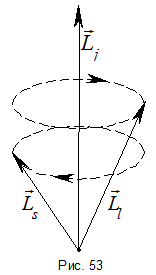
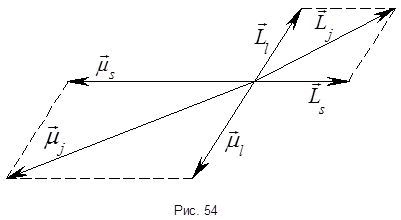
Полный магнитный момент электрона равен сумме векторов орбитального магнитного момента и спинового магнитного момента:  . Так как
. Так как  . Таким образом, гиромагнитное отношения для механических и магнитных моментов различны. Поэтому полный механический и полный магнитный момент не коллинеарны.
. Таким образом, гиромагнитное отношения для механических и магнитных моментов различны. Поэтому полный механический и полный магнитный момент не коллинеарны.
1 См. лекции по теоретической механике под редакцией Ерыкалина А. В.






















