- Основные этапы моделирования

Основные этапы моделирования.

При изучении сложных систем, исследованный объект может быть заменен другим, более простым, но сохраняющим основное более существенное для данного исследования свойства. Такой объект- модель. Моделирование- это метод, при котором производится замена изучения некоторого сложного объекта исследованием его модели. Основные этапы моделирования:

1. Первичные сбор информации; для построения моделирования необходимо получить как можно больше информации о разнообразных характеристиках данного объекта, о его свойствах, закономерностях поведения при различных внешних условиях;

2. Постановка задач; формируется цепь исследования, основные его задачи, определяется какие новые значения может получить исследователь в результате моделирования;

3. Обоснование основных упрощений; выделяется существенное для данных целей характеристики, а так же те факторы, которыми можно пренебречь;

4. Создание модели и ее исследование;

5.  Проверка адекватности модели реальному объекту, указание границ применимости модели.

В биофизике, биологии, медицине принимают физические, биологические, математические модели, так же используется аналоговое моделирование. Физическая модель имеет физическую природу, часто такую же, что и исследуемого объекта, например, течение крови по сосудам моделируется течением жидкости по трубкам. Физические устройства, вероятно, заменяющие органы живого организма, так же можно отнести к моделям. Направление в технике, использование физической модели для технических решений называется бионикой. Биологические модели представляют собой биологические объекты, удобные для экспериментальных исследований, ан которых изучаются свойства, закономерности биофизических пространств в реальных сложных объектах. Математические модели представляют собой описание процессов в реальных объектах с помощью математических уравнений, как правило дифференциальных. Для реализации математических моделей широко используются компьютеры. При помощи системы моделей можно легко изменить масштаб времени, ускорить и замедлить течение пространств, рассмотреть процессы в стационарном режиме, либо изменить конфигурацию зоны патологии. Изменяя коэффициенты или вводя новые параметры в дифференциальные уравнения можно учитывать различные свойства моделирующего объекта или теоретически создать объекты с с новыми свойствами. С помощью компьютера можно решать сложные уравнения и прогнозировать поведение системы: течение заболевания, эффективность лечения, действие лекарственных препаратов. Если процессы в моделировании имеют другую физическую природу, чем у оригинала, но описывается таким же математическим аппаратом, то такая модель называется аналоговой. Основные требования, которым должна отвечать модель:

Рекомендуемые материалы

1. адекватность- соответствие модели объекту. Это значит, что модель должна с заданной степенью точности воспринимать закономерности изучающих явлений. Анализ адекватности должен производится как при выборе модель, так и при сравнении результатов моделирования с реальным поведением объекта.

2.  Должны быть устранены границы применяемости модели, т.е. четко заданы условия, при которых выбранная модель адекватна исследуемому объекту.

Результатом моделирования является получение новых данных о протекании изучаемого процесса и его свойствах. Результаты моделирования не дают исчерпывающих сведений об изучаемом объекте, но углубляют знания о его свойствах. В медико-биологических исследованиях применяют «метод черного ящика», т.е изучая только входящие и выходящие параметры исследуемого объекта без учета его внутренней структуры и внутренних процессов. В этом случае изучается зависимость выходных параметров от входных, т.е получают передаточную информацию. В основе процессов обмена клетки со средой и внутренних параметров жизнедеятельности лежит сложная сеть различных реакций. В биологической системе каждый элемент находит в постоянном и неразрывном взаимодействием друг с другом, что в основном определяет природу динамического поведения структур, механизмы их саиорегуляции и управления. В результате динамических процессов изменяется концентрация различных веществ, численность отдельных клеток, биомасса организма, могут изменится и другие параметры. Например, мембранный потенциал клетки. Изменение переменных величин в каждый момкнт времени могут быть описаны соответствующими дифференциальными уравнениями. Рассмотрим пример замкнутой популяции клеток, в которой одновременно происходят процессы размножения и гибели клеток. Пусть в некоторый момент времени концентрация клоток в среде ровна N, тогда скорость изменения числа клеток определяется   

Решая д.у. можно ответить на вопрос как меняется численность клеток, возможно ли в такой системе устронение стационарного состояния, когда численность клеток не меняется. В простом случае скорость размножения, скорость гибели будет пропорционально числу клеток: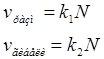

 И д.у. будет иметь вид

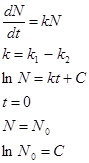
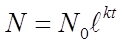
В зависимости соотношение констант скорости гибели и скорости размножения судьба этой замкнутой популяции будет различна:

1. Если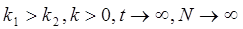 

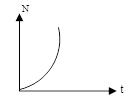
  2.Если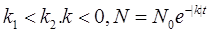

   3.Если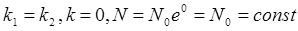

В отличие от обычной химической кинематики, биологическая кинематика характеризуется следующими особенностями:

1. В качестве переменных рассматривается не только концентрация веществ, но и другие велечины.

2. Перемещения изменяется не только во времени, но и в пространстве,

3. Биологическая система гетерогенна, т.е.в разных точках системы условия взаимодействия между величинами могут быть различными,

4. Существует специальный механизм саиорегуляции действующие по принципу обратные связи.

Обычно в качестве модели открытой системы используется гидродинамическая модель сосуда, в который одновременно вливается и вытекает жидкость. Уровень жидкости в сосуде зависит от соотношения скоростей притока и оттока жидкости. При равенстве этих скоростей, уровень жидкости постоянен, т.е. возникает стационарное состояние. Изменение скорости притока и оттока приводит к выходу системы из стационарного состояния. Используем такую систему для описания существования клетки, в которой происходит обмен веществ с окружающей средой. Пусть происходит поступление в клетку вещества из резервуара с постоянной концентрацией.

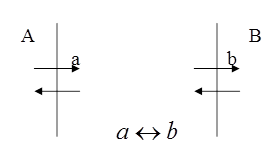
а и b переменные концентрации вещества внутри системы, А B постоянные концентрации этих же веществ во внешних резеркуаарах. Кроме того, существуют константы скоростей процессов поступления вещества в клетку  и оттока продукции реакции продукта , а  так же константы скоростей взаимодействия. Уравнения кинетики для этой системы можно представить в виде д.у.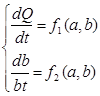

Поскольку в стационарном состоянии a u b принимают постоянные значения, то левая часть этого уравнения обращается в 0.

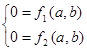
Система алгебраических уравнений, решением которой будут стационарное значение концентраций веществ  и . Эти величины не зависят от начальных условий и определяются только величинами констант и концентрацией вещества во внешних резервуарах. это означает, что в каком бы начальном состоянии не находилась бы система е ней устанавливается один стационарный режим. Т.о. анализ кинематической задачи сводится не к точному решению д.у., а к поиску тех стационарных режимов в которых система может находится. Т.о. качественный анализ модели заключается в получении характеристик динамического поведения системы, т.е. в определению устойчивых и не устойчивых стационарных состояний, переходов между ними, выявление колебательных режимов. Важной характеристикой решения является установленной стационарной точки. Рассматривая малые отклонения параметров стационарного состояния и разлогая в ряд Тейлора функцию по данному параметру можно ввести условие устойчивости.

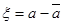
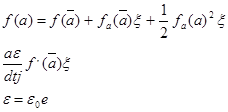
Если произведение правой части уравнения стационарной точки отрицательно, то отклонение от стационарного состояния  

1)         

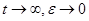
Если произведение положительно, то данное состояние является неустойчивым при  длительном отклонении от стационарного состояния стпнет  но большем. Т.о. знак произведений правой части д.у. в стационарной точке указывает на характер установленного стационарного состояния. Т.о. важное свойство системы можно выявить изучая свойство правых частей д.у., не прибегая к их точному аналитическому решению. Однако такой подход возможен при исследовании моделей, содержащие не большое число переменных, отражающих наиболее важное динамическое свойство. Кроме того, редукция числа уравненийоснована на принципе «узкого шеста  или принципа разделение всех переменных во всех системах на быстрые и медленнее». Медленные процессы можно считать постоянными и число уравнений в этом случае сокращается  т.о. производится редукция только тех уравнений которые оказываюм воздействие на переменные в данный момент времени. Современная практика математического моделирования показывает, что наиболее содержимыми являются модели, использующие как правило, два уравнения. Т.е. пользуясь редукцией системы уравнения исходную модель можно свести к виду:

Для такой системы используются конечные методы исследование системы д.у. Одним из методов исследования системы Д.У - метод фазовых плоскостей для системы с двумя переменными эта плоскость ху. Такая плоскость является фазовой, а точка - изображения. В каждый момент времени каждая точка будет двигается в соответствии системы Д.у.

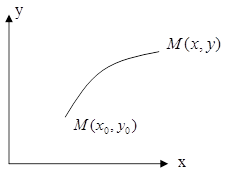
 Совокупность этих точек образует фазовую траекторию. Наиболее важным является характер фазовой траектории в близи стационарной точки. Согласно определению стационарного состояния в особой точки правой части уравнения равны 0. Для нахождения особой точки, необходимо построить на фазовой плоскости кривые p(x,y)=0 и Q(х,у)=0, точка пересекающая эти кривые и будет особой точкой, а ее координаты определяют стационарное значение переменных. Важной характеристикой системы являются устойчивость стационарных состояний. Для получения решения этой задачей необходимо задать небольшое отклонение от переменных для стационарных состояний и подставить их в Д.У; разложить в ряд Тейлора каждую из функций получен для малого параметра:

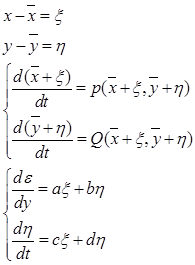
для определения характера устойчивости, необходимо одновременного учитывать поведение во время отклонений по обеим переменным. Однако, эти отклонения изменяются со временем по разным законам. И следовательно, в окрестностях с собой точках фазные траектории будут изменятся в зависимости от характера изменения обеих переменных. Решение системы уравнений будет  В виде exp-m.

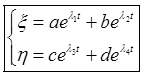
показатели exp-m будут определяться из характерного уравнения. В зависимости от знака и величины покрытия exp-m поведение переменных в близи окрестности особой точки будут разлины. В случае если действительные части покрывающей exp-m положительны, то амплитуда колебаний со временем нарастает и особая точка имеет вид неустраненого фокуса.

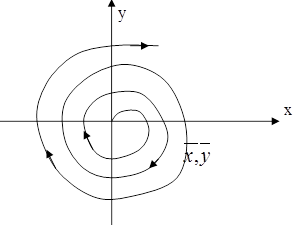
В случае если Re части покрывающей exp-m раны нулю, то сами покрытия являются .... числами, которые не проходят через особую точку. Небольшие возмущения переводят в систему с одной эксцентрической траектории на другую, при этом изменяется амплитуда колебаний. В этом случает особая точка - центр.

Бесплатная лекция: "2 Тенденции развития СМИ в Вологодской области" также доступна.

Первые пять типов особых точек описывают соотношения равновесия, не меняющиеся при изменении правой части уравнения в случае "центра" небольшие изменения правых частей Д.У легко нарушают условия равновесия, тем самым изменяя сам тип устойчивости, приводя к появлению в системе других особых точек. Первичное возмущение системы возникает неустановленных моделях за счет случайных процессов, нарастает по амплитуде и ограничивается за счет нескольких процессов. В итоге система может проходить в установленное стационарное состояние. Сам процесс перехода из одного установленного состояния в другое в результате неустановлености первого состояния называется бифуркацией. Процесс бифуркации лежит в основе самоорганизации биологических систем, т.е самопроизвольного возникновения установленных структур. Условия необходимые для возникновения самоорганизации систем:

1.Система должна быть открытой

2.Динамическое уравнение, описывающее процессы в системе, должны быть не линейным.

3. Отклонение от установленного состояния должно превышать критическое значение.

4.Микроскопические процессы в системе происходят самосогласованно, т.е коллективно.

Наука изучающая процессы саморегуляции, т.е механизмы описывающих возникновения и распространения структур в однородной системе с диффузией, либо с другими процессами релаксации. Примерами самоорганизации является реакция Жопотинского - Белоусова в химии.