Оценка коэффициента интенсивности напряжений

Оценка коэффициента интенсивности напряжений

14.1. Аналитические методы

В настоящее время аналитическими методами теории упругости решено большое количество задач для различных конфигураций твердого тела, трещины и условий нагружения.

Плоские статические задачи. В задачах о плоской деформации и плоском напряженном состоянии КИН определяются по асимптотике комплексного потенциала Ф(z) в конце разреза.

Разрезы вдоль одной и той же прямой или вдоль одной и той же окружности в бесконечной упругой плоскости. Если совокупность математических разрезов расположена вдоль одной и той же прямой или вдоль одной и той же окружности и других границ упругое тело не имеет, то могут быть решены следующие краевые задачи:

а) на разрезах произвольно задана нормальная и касательная нагрузка;

б) на разрезах заданы произвольные смещения;

в) на одном берегу разрезов задаются смещения, а на другом берегу – нагрузки;

г) участки с произвольно заданными смещениями или нагрузками чередуются любым образом вдоль нижнего и верхнего берегов разрезов;

Рекомендуемые материалы

д) берега разрезов взаимодействуют, причем касательное напряжение взаимодействия произвольным образом зависит от нормального давления;

е) касательное напряжение на разрезах обращается в нуль, участки с произвольно заданным нормальным смещением  или с нормальной нагрузкой расположены произвольно на берегах разрезов.

Для указанных типов задач можно найти КИН; некоторые случаи рассмотрены ниже.

Если в упругой плоскости имеется один прямолинейный разрез и сосредоточенные сила и момент приложены симметрично к верхнему и нижнему берегам щели (рис. 47), то

.

Для распределенных на некотором участке верхнего берега щели нагрузок (рис. 48) имеем

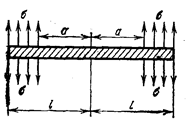
Рис. 47                                       Рис. 48                                     Рис. 49

.

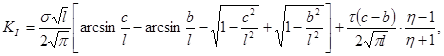
В случае, изображенном на рис. 49, имеем

.

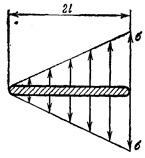
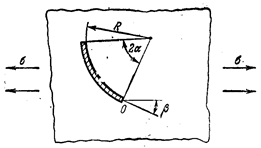
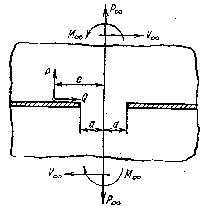
Рис. 50                                     Рис. 51                                   Рис.  52

Для примера на рис. 50 на правом и левом конце соответственно

.

Для щели, располагающейся вдоль длины окружности (рис. 51), КИН в наиболее опасной точке О имеют вид

.

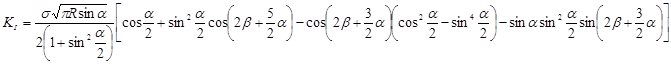
В случае перешейка между двумя полубесконечными щелями имеют место следующие формулы

- у левого конца перешейка

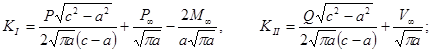
- у правого конца перешейка

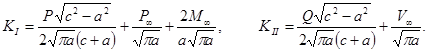
Разрез в полуплоскости. Задача о растяжении упругой полуплоскости с краевой щелью (рис. 53) рассматривалась многими авторами. Ее решение получено многими способами – как точными аналитическими методами, так и приближенными:

.

Коэффициент 1.12 вычислен с погрешностью 1%. Как видно, влияние свободной границы тела приводит к увеличению КИН на 12%.

Для задачи на рис. 54

.

Коэффициент 0.68 вычислен с ошибкой 3%.

В случае полубесконечного разреза, приближающегося к свободному краю полуплоскости (рис. 55) КИН равен

.

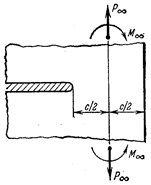
Рис. 53                                Рис. 54                                      Рис. 55

Разрезы, исходящие из круглого отверстия. Решена задача о всестороннем и одностороннем растяжении плоскости с одной и двумя щелями, исходящими из кругового отверстия (рис. 56).

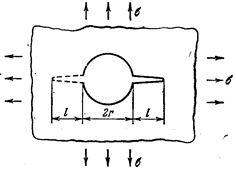
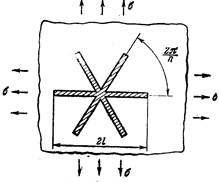
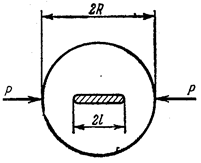
Рис. 56                                           Рис. 57                                   Рис. 58

Имеем

.

Решена задача о всестороннем растяжении плоскости со звездообразной щелью (рис. 57). Окончательный результат имеет вид

,

где x(т) – коэффициент, зависящий от числа разрезов n.

Для круглого диска с внутренней щелью, раздавливаемого двумя сосредоточенными силами (рис. 58),

.

 Рис.  59.

Тела сложной формы. Изучены многие случаи различных криволинейных отверстий со щелями. В случае всестороннего растяжения упругой плоскости с гипоциклоидальным отверстием, контур которого описывается уравнениями

,

где n – целое положительное число, КИН равен

.

Гипоциклоида имеет n+1 точку возврата, каждая из которых с точки зрения концентрации напряжений эквивалентна концу трещины (на рис. 59 изображена астроида с n=3).

Пространственные задачи. В силу сложности решения пространственных задач готовых решений накоплено значительно меньше, чем для плоского случая. Приведем окончательные результаты вычисления КИН в пространственных задачах.

Дискообразная щель. В общем осесимметричном случае дискообразного разреза вдоль z=0, x²+y²<a² в безграничном пространстве (рис. 60) имеем

 Рис. 60.

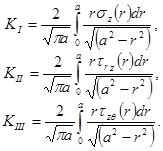
Здесь предполагается, что нагрузки симметрично приложены к верхнему и нижнему берегам щели, а на бесконечности напряжения исчезают.

При чистом изгибе стержня с дискообразной щелью (рис. 61) КИН будет следующим

.

Здесь J_y – соответствующий момент инерции поперечного сечения стержня, b – расстояние центра щели от нейтральной линии.

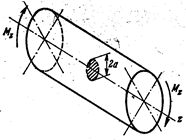
Рис. 61                                                        Рис. 62

При скручивании круглого цилиндрического стержня с дискообразной щелью (рис. 62) имеем (здесь предполагается, что центр щели лежит на оси стержня, а плоскость щели перпендикулярна этой оси)

.

Итак, имеется большое количество решенных аналитическим способом задач по определению КИН для тел с трещинами различной конфигурации, но все же число этих задач ограничено.

14.2. Метод конечных элементов

В настоящее время известны различные методы расчета КИН, использованные на использовании МКЭ. Они имеют свои преимущества и недостатки. Рассмотрим некоторые из них.

14.2.1.Прямой метод

В этом случае для определения КИН в асимптотические формулы для компонент напряжений и перемещений в вершине трещины непосредственно подставляют возникающие в окрестности вершины трещины напряжения или перемещения, полученные с помощью МКЭ. При использовании напряжений этот способ называется прямым методом напряжений, а при использовании перемещений – прямым методом перемещений. Значения напряжений или перемещений, которые необходимо подставить в формулы, следует выбирать такими, чтобы они были определяющими для рассматриваемого типа деформирования. Например, в случае трещины типа I необходимо подставить компоненту напряжения s_y, которая действует на оси х в направлении оси у. По сравнению с методом напряжений метод перемещений дает более надежные результаты с точки зрения точности.

Расчет КИН прямым методом требует, чтобы решение для напряжений и перемещений имело достаточно высокую точность в окрестности вершины трещины. При использовании обычных элементов нельзя отразить особенность при приближении непосредственно к вершине трещины. Поэтому нельзя ожидать, что точность расчета напряжений и деформаций в окрестности вершины трещины будет высокой. Следовательно, установленные по этим параметрам КИН также будут иметь не слишком хорошую точность. Поэтому при определении КИН с помощью обычных элементов необходимо предусмотреть меры, позволяющие улучшить точность решения. К таким мерам можно отнести следующие.

(1) У вершины трещины, насколько это возможно, желательно использовать разбиение на малые элементы (мелкую дискретизацию).

(2) Часто могут возникать ситуации, например при решении трехмерных задач, когда разбиение на мелкие элементы оказывается нерациональным с точки зрения вычислительных ресурсов. В таких случаях сначала находят решения для грубого разбиения, а затем выделяют окрестность вершины трещины, выполняют мелкое разбиение и решают задачу. При этом в качестве граничных условий используют перемещения узлов и узловые силы, полученные в предыдущем решении. Такой способ решения называют поэтапным.

(3) Используя асимптотические формулы для компонент напряжений и перемещений в вершине трещины, в точках, расположенных на различных расстояниях r от вершины трещины, расчетным путем определяют значения К и строят график зависимости К от r. Искомое значение К, соответствующее рассматриваемой трещине, принимают равным тому значению, которое получается в результате экстраполяции при  r ® 0 (рис. 63). Следует иметь в виду, что значения К, соответствующие точкам, наиболее близко расположенным к трещине, обладают не очень хорошей точностью. Поэтому при проведении экстраполяции эти значения исключают.

1.

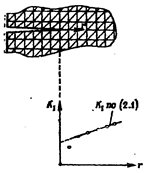
2. Рис. 63. Оценка КИН путем экстраполяции

(4) Используют всевозможные разбиения от грубых до мелких и определяют значения К, проводя так же, как в п. 3, экстраполяцию при r ® 0.

В пп. (1) и (3) дискретизация выполняется один раз, а в пп. (2) и (4) – несколько раз, что затрудняет решение задачи. Пункты (1) и (3), а также их сочетание можно отнести к таким методам оценки К, когда необходимо, используя обычные элементы и не выделяя особенностей, довольно быстро определить КИН. В других случаях необходимо использовать специальную дискретизацию.

14.2.2. Энергетический метод

Известно несколько энергетических методов, наиболее распространенным из которых является метод полной энергии. Интенсивность G освобождения энергии, которое имеет место при распространении трещины в упругом теле, связана с КИН зависимостью

.

При распространении трещины на величину dА изменение энергии деформации составляет dU. Интенсивность освобождения энергии можно также представить как G=dU/dА. Таким образом, если в результате использования МКЭ установить интенсивность освобождения энергии G, можно определить КИН. Однако видно, что найденный таким образом КИН должен относиться к трещине одного из типов, т.е. для этих типов трещин расчет К возможен только порознь.

При определении интенсивности освобождения энергии можно воспользоваться изложенными ниже двумя способами.

А. Методом конечных элементов проводят численное решение для трещины площадью А. При этом определяют энергию упругой деформации U(A). Затем рассматривают рост трещины на один элемент. При тех же граничных условиях вновь МКЭ решают задачу и определяют U(A+dА). Тогда G=( U(A+dА) - U(A))/ dА. Энергию упругой деформации можно установить путем интегрирования энергий деформации в отдельных точках по всей рассматриваемой области. Полученное значение должно быть равно работе внешних сил. Однако расчет работы внешних сил довольно прост и позволяет исключить сложности, связанные с интегрированием.

Б. Можно не рассматривать рост трещины на один элемент, а за счет соответствующего смещения координаты вершины трещины задавать ее распространение (рис. 64). В результате такой операции будет происходить изменение жесткости. При этом можно считать, что жесткость меняется лишь у тех элементов, которые окружают вершину трещины. Если принять это во внимание и путем исключения решать систему линейных уравнений, можно за одно решение определить dU= U(A+dА) - U(A). При этом необходимо в процессе исключения вначале соответствующим образом вводить указанную операцию распространения трещины.

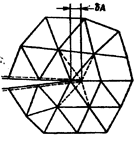
3. Рис. 64. Виртуальный рост трещины

В случае использования метода А необходимо по отдельности дважды проводить решение. В рассматриваемом же методе в этом нет необходимости. Его можно эффективно использовать при большом числе уравнений, в частности при решении трехмерных задач. Метод Б носит название метода виртуального роста трещины, а метод А – метода податливости.

14.2.3. Использование специальных элементов

4. Методы, использующие аналитические решения.  На рис. 65 изображен треугольный элемент с трещиной, предложенный Бисковым. В качестве решения вводится решение, полученное из функции напряжений Мусхелишвили. При этом аналитическое решение имеет особенность напряжений, характерную для вершины трещины. В случае такого элемента восьми степеням свободы узлов соответствует восемь независимых переменных: три переменные, характеризующие перемещения твердого тела, три средних напряжения и КИН К_I  и К_II.

5.

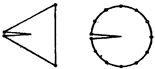
6. Рис. 65. Специальные элементы Бискова и Уилсона

Руководствуясь аналогичными соображениями, Уилсон предложил круглый элемент с трещиной (рис. 65) и нашел решение, используя до высоких порядков разложение функции перемещения в окрестностях трещины.

Необходимо отметить, что при использовании этих элементов в реальных условиях обычно их окружение составлено из треугольных элементов. При этом обеспечиваются такие условия, при которых перемещения смежных элементов в узлах совпадают, однако в общем случае не выполняется условие неразрывности перемещений на границах элементов, за исключением узлов. Поэтому не существует теоретического обоснования сходимости. Тем не менее, численные эксперименты показали, что при этом не возникает существенных проблем.

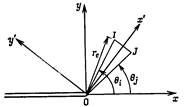
Рис. 66. Специальный элемент Уилсона

Методы, использующие простые функции для описания особенностей. На рис. 66 показан предложенный Уилсоном элемент, представляющий собой равнобедренный треугольник, вершина которого находится в вершине трещины. Для этого элемента перемещение можно представить таким образом

Лихачев Д.С. Слово о полку Игореве - героический пролог русской литературы - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.

.

Аналогично можно определить перемещение v. Такой элемент для напряжений и деформаций имеет особенность в вершине трещины.

Деформированные изопараметрические элементы. У обычного восьмиузлового изопараметрического элемента узлы находятся на серединах сторон. Если сместить узлы в точки, соответствующие ¼ длины стороны, то можно получить особенность в вершине трещины (рис. 67). Однако в этом случае будет отсутствовать сходимость решения и энергия деформации будет иметь особенность в вершине трещины. В связи с этим предложено считать длину одной из сторон четырехугольника равной нулю. В результате объединения смежных узлов удалось получить элемент, который одновременно обладал всеми необходимыми свойствами (рис. 67).

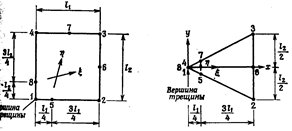
7. Рис. 67.  Деформированные элементы

Такой элемент может быть использован как для упругого тела, так и для идеально пластического без деформационного упрочнения.