Кривые второго порядка

13. Приложения определенного интеграл.

13.1. Некоторые кривые, которые будут встречаться в дальнейшем.

            В этом разделе мы рассмотрим некоторые приложения определённого интеграла, в основном, геометрические - к вычислению площадей и объёмов. Здесь мы приведём уравнения и изображения ряда кривых, которые с которыми будем работать дальше.

1. Окружности, проходящие через начало системы координат. Уравнение окружности с центром

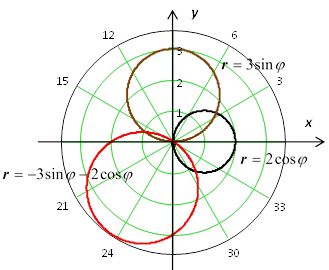
 радиуса : . Если окружность проходит через начало координат, то , и уравнение принимает вид  . В полярных координатах это уравнение выглядит так: . На рисунке справа приведены три такие окружности  (),  (), ().

2. Спирали: спираль Архимеда . На рисунке изображены спирали  и . Логарифмическая спираль . На рисунке изображены спирали  и .

Гиперболическая спираль . На рисунке изображены спирали  и . Стрелками на всех спиралях указано направление возрастания параметра .

3. Кардиоида . Три таких кривых изображены на рисунке справа.

Рекомендуемые материалы

Декартово уравнение кардиоиды: ;

Параметрические уравнения кардиоиды:

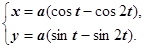
Кардиоида - частный случай улитки Паскаля .

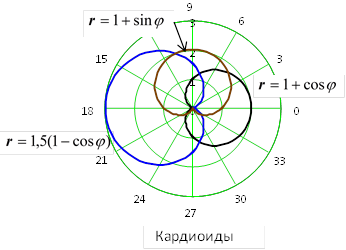
4. Лемниската Бернулли . 

Подкоренное выражение неотрицательно при  и  . Декартово уравнение лемнискаты .

Лемниската - геометрическое место точек  таких, что , где  и  - фокусы лемнискаты.

На рисунке изображена лемниската с .

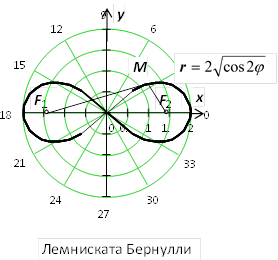
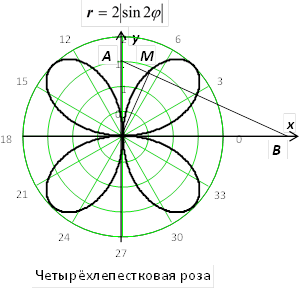
5. Четырёхлепестковая роза . Декартово уравнение .

Каждая точка  этой кривой - основание перпендикуляра , опущенного из начала координат на отрезок постоянной длины , движущийся так, что его концы находятся на осях координат.

6. Развёртка (эвольвента) окружности

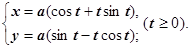
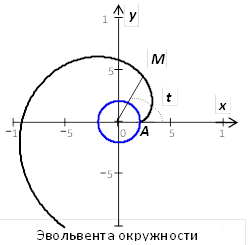
Каждая точка  этой кривой - конец нити, которая разматывается с окружности , оставаясь в натянутом состоянии. В начальный момент   конец нити находится в точка .

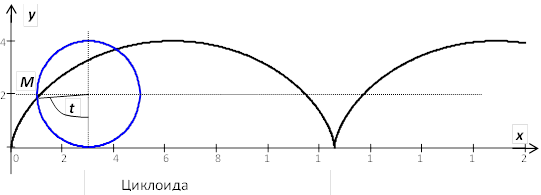
7. Циклоида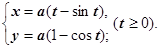

Эта кривая - траектория точки  окружности радиуса , которая без скольжения катится по оси . В начальный момент   точка находится в точка .

8. Астроида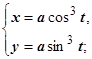

Люди также интересуются этой лекцией: Лекция 3.

Декартово уравнение . Каждая точка  этой кривой - основание перпендикуляра , опущенного из начала координат на отрезок постоянной длины , движущийся так, что его концы находятся на осях координат. Точка - вершина прямоугольника, построенного на отрезке  как диагонали. На рисунке приведена астроида с .

.

.

.

.

.