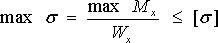Расчет заклепок на смятие и листов на разрыв

ЛЕКЦИЯ №24

Расчет заклепок на смятие и листов на разрыв.

Помимо среза заклепкам и соединяемым листам в конструкции угрожают и иные опасности.

Так как передача сил на заклепочный стержень происходит путем нажатия стенок заклепочного отверстия на заклепку, то необходимо установить, не произойдет ли наружное обмятие этого стержня или стенок отверстия, — произвести проверку на смятие.

На рис.1 указана примерная схема передачи давлений на стержень заклепки. Закон распределения этих давлений по цилиндрической поверхности нам неизвестен; он во многом зависит от неправильностей формы заклепочного отверстиями стержня, вызванных условиями изготовления конструкции. Поэтому расчет производится условно. Принято считать, что неравномерное давление, передающееся на поверхность заклепки от листа, распределяется равномерно по диаметральной плоскости сечения заклепки. При этом напряжение по этой диаметральной плоскости оказывается примерно равным наибольшему сминающему напряжению в точке А поверхности заклепки.

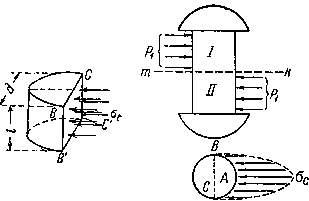
Рис.1 Передача давлений на стержень заклепки.

Чтобы вычислить это условное напряжение смятия, необходимо разделить силу, приходящуюся на заклепку, на площадь диаметрального сечения ВСС'В'. Эта площадь представляет собой прямоугольник, одной стороной которого служит диаметр заклепки, другая же равна толщине листа, передающего давление на стержень заклепки.

Так как давление на одну заклепку равно , то

Рекомендуемые материалы

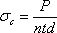
условие прочности на смятие будет иметь вид:

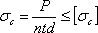
где — допускаемое напряжение на смятие. Отсюда необходимое число заклепок

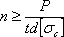
Допускаемое напряжение на смятие принимают обычно в 2 — 2,5 раза больше основного допускаемого напряжения на растяжение и сжатие , так как расчет на смятие по существу является упрощенной проверкой прочности по контактным напряжениям.

Таким образом определяется число заклепок, необходимое для прочного соединения листов. Из двух полученных значений , конечно, надо взять большее.

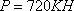
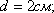
Если мы вернемся к рассмотренному ранее примеру и примем , ,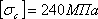то получим:

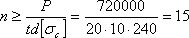
Таким образом, условие прочности заклепок на перерезывание требует постановки двадцати четырех заклепок; условие же прочности на смятие — пятнадцати заклепок. Очевидно, необходимо поставить двадцать четыре заклепки. В этом примере работа заклепок на срез оказывается опаснее работы их на смятие. Это обычно бывает в соединениях с так называемыми односрезными заклепками, в которых каждая заклепка перерезывается в одной плоскости.

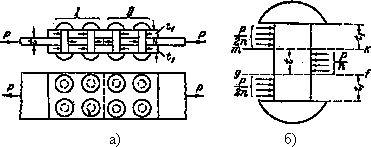
а) расчетная схема, б) действующие усилия

Рис. 2 Соединение с накладками:

В несколько других условиях будут работать заклепки соединения, показанного на Рис.2а. Здесь стык двух листов осуществлен при помощи двух накладок. Сила Р при помощи первой группы заклепок передается от левого листа обеим накладкам, а от последних при помощи второй группы заклепок передается правому листу.

Называя через число заклепок, необходимое для передачи усилия Р от листа на накладки и от накладок на другой лист, получаем, что на каждую заклепку передается усилие от основного листа . Оно уравновешивается усилиями , передающимися на заклепку от накладок (Рис.2б).

Стержень заклепки теперь подвергается перерезыванию уже в двух плоскостях; средняя часть заклепки сдвигается влево. Допускают, что срезывающая сила равномерно распределяется по двум сечениям, и gf. Напряжение и условие прочности для двухсрезной заклепки принимает вид:

и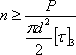

Таким образом, при двойном перерезывании число заклепок по срезыванию оказывается в два раза меньше, чем при одиночном перерезывании.

Переходим к проверке на смятие. Толщина склепываемых листов ; толщина накладок не должна быть меньше 0,5t, так как две накладки должны взять от основного листа всю силу Р. Поэтому:

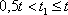
Сила сминает и среднюю часть заклепки и верхнюю с нижней. Опаснее будет смятие той части, где площадь смятия меньше.

Так как толщина среднего листа не больше суммы толщин обеих накладок, то в худших условиях по смятию будет средняя часть заклепки. Условие прочности на смятие останется таким же, как и при односрезных заклепках:

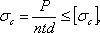
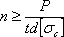
Таким образом, для рассматриваемой конструкции число заклепок в первой и во второй группах определится из полученных условий.

Пусть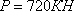

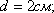
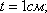
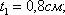
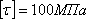
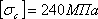
Тогда:

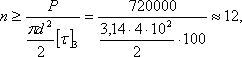
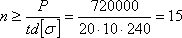
В этом случае при двухсрезных заклепках условия их работы на смятие тяжелее, чем на срезывание; следует принять .

На двух рассмотренных примерах мы установили общие методы проверки прочности заклепочных соединений. В металлических конструкциях иногда приходится склепывать целые пакеты соединяемых элементов. В таких пакетах заклепки могут работать и на большее число срезов. Однако методы расчета многосрезных заклепок не отличаются от изложенных. Для вычисления касательных напряжений следует разделить силу, относящуюся к одной заклепке, на суммарную площадь среза, воспринимающую эту силу. Для вычисления же напряжений смятия следует найти ту часть заклепки, которая находится в наиболее опасных условиях, т. е. воспринимает наибольшую силу на наименьшем протяжении. Напряжения смятия получаются делением этой силы на площадь диаметрального сечения наиболее напряженной части заклепки. Затем останется написать два условия прочности и получить .

Наличие заклепок вносит некоторые изменения и в проверку прочности на растяжение или сжатие самих склепанных листов. Опасным сечением каждого листа (Рис.3) будет теперь сечение, проходящее через заклепочные отверстия; здесь рабочая ширина листа будет наименьшей; принято говорить, что это сечение ослаблено заклепочным отверстием. Называя полную ширину листа b, получаем для него такое условие прочности:

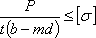
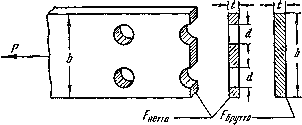
Рис. 3 Расчетная модель листа на разрыв.

где — число отверстий, попадающих в сечение (в нашем случае — два).

Отсюда можно найти величину , задавшись толщиной листа t. Площадь ослабленного сечения называется площадью нетто, площадь же полного сечения листа называется площадью брутто.

Этот учет влияния заклепочных отверстий на прочность склепываемых листов общепринят, но является весьма условным. На самом деле, влияние отверстия в листе вызывает у его краев, на концах диаметра, перпендикулярного к направлению растяжения, значительные местные напряжения, которые могут достичь предела текучести материала и вызвать остаточные деформации, захватывающие, однако, весьма небольшой объем материала листа.

Некоторую опасность в отношении образования трещин эти местные напряжения могут представить лишь при действии переменных нагрузок в материале, имеющем низкий предел усталости. Однако в обычных условиях работы заклепочных соединений эта опасность может считаться исключенной. Во избежание возможности разрушения листов заклепками заклепки размещаются на определенных расстояниях друг от друга и от края листа.

Расположение заклепок в плане производится как по условиям обеспечения прочности и плотности соединения, так и по чисто производственным соображениям. Расстояния между центрами заклепок принимаются не менее 3d и не более 7d. Расстояния до края листов должны быть не менее (Рис.4). Чтобы длина стыка была возможно меньше, берут , а в целях меньшего ослабления сечения расстояние е берут возможно большим (до 7d), что позволяет уменьшить число рядов, а следовательно, и ослабление.

Рис.4 Практические рекомендации по расположению заклепок в соединении.

При проектировании заклепочных соединений для котлов и резервуаров, где добиваются плотных швов, помимо расчета на срез производят проверку сопротивления скольжению за счет трения. Однако допускаемое напряжение по скольжению дается в МПа поперечного сечения заклепки; таким образом, проверка на трение при односрезных заклепках сводится к проверке на срез лишь с другим допускаемым напряжением. При двухсрезных заклепках в расчет на трение вводится, конечно, одна площадь сечения заклепки, но зато повышается почти вдвое допускаемое напряжение на трение за счет двух накладок.

Поэтому так называемый расчет заклепок на трение является, по существу, проверкой прочности на срез с другими лишь допускаемыми напряжениями на квадратный сантиметр площади поперечного сечения заклепки.

Правильнее было бы сохранить лишь один метод проверки заклепочных соединений на смятие и срез, учитывая влияние сил трения при назначении допускаемых напряжений в зависимости от способа клепки, качества отверстий и требований, предъявляемых ко шву в отношении плотности.

В заклепочных соединениях для котлов принимают обычно допускаемое напряжение на скольжение (на 1 см² площади заклепки):

· от 50 до 70 МПа при швах внахлестку,

· 90 120 с двумя накладками.

При проверке по этим данным, очевидно, надо вести расчет, как при заклепках одиночного перерезывания, с допускаемым напряжением от 50 до 70 или от 90 до 120МПа.

Прямой поперечный изгиб стержня

При прямом поперечном изгибе в сечениях стержня возникает изгибающий момент М_х и поперечная сила Q_y рис. 1), которые связаны с нормальными и касательными напряжениями

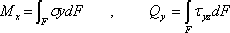
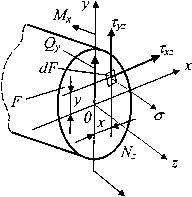
Рис.1 Связь усилий и напряжений

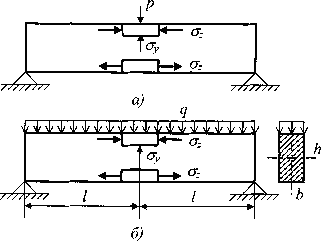
а) сосредоточенная сила, б) распределенная

Рис.2 Модели прямого поперечного изгиба:

Выведенная в случае чистого изгиба стержня формула для прямого поперечного изгиба, вообще говоря, неприменима, поскольку из-за сдвигов, вызываемых касательными напряжениями , происходит депланация поперечных сечении (отклонение от закона плоских сечений). Однако для балок с высотой сечения h<l/4 (рис. 2) погрешность невелика и ее применяют для определения нормальных напряжений поперечного изгиба как приближенную. При выводе условия прочности при чистом изгибе использовалась гипотеза об отсутствии поперечного взаимодействия продольных волокон. При поперечном изгибе наблюдаются отклонения от этой гипотезы:

а) в местах приложения сосредоточенных сил. Под сосредоточенной силой напряжения поперечного взаимодействия могут быть достаточно велики и во много раз превышать продольные напряжения , убывая при этом, в соответствии с принципом Сен-Венана, по мере удаления от точки приложения силы;

б) в местах приложения распределенных нагрузок. Так, в случае, приведенном на рис. 2, б, напряжения от давления на верхние волокна балки . Сравнивая их с продольными напряжениями , имеющими порядок

,

приходим к выводу, что напряжения при условии, что h² <<l², так как .

Получим формулу для касательных напряжений . Примем, методика расчета нормальных напряжений известна, что касательные напряжения равномерно распределены по ширине поперечного сечения (рис. 3). Эта предпосылка выполняется тем точнее, чем уже поперечное сечение стержня. Точное решение задачи для прямоугольного поперечного сечения показывает, что отклонение от равномерного распределения , зависит от отношения сторон b/h. При (b/h) =1,0 оно составляет 12,6%, при (b/h) =0,5 — только 3,3%.

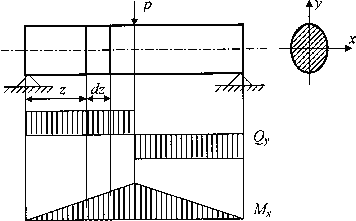
Рис.3. Расчетная модель поперечного прямого изгиба

Непосредственное определение напряжений затруднительно, поэтому находим равные им (вследствие закона парности) касательные напряжения , возникающие на продольной площадке с координатой у элемента длиной dz, вырезанного из балки, (рис. 3). Сам элемент показан на рис. 4. От этого элемента продольным сечением, отстоящим от нейтрального слоя на у, отсекаем верхнюю часть, заменяя действие отброшенной нижней части касательными напряжениями (индекс гу в дальнейшем опускаем), равнодействующая которых показана на рис. 5. Здесь, согласно второй предпосылке

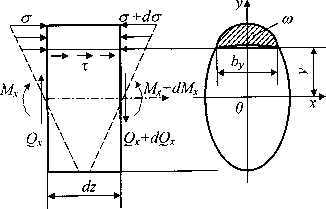
Рис.4 Расчетный элемент бруса

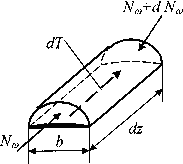
Рис.5 Фрагмент расчетного элемента бруса

по ширине элемента b. Нормальные напряжения и , действующие на торцевых площадках элемента, также заменим их равнодействующими

,

.

Согласно первой предпосылке нормальные напряжения определяются уже известным способом, , где —статический момент отсеченной части площади поперечного сечения относительно оси Ох.

Рассмотрим условие равновесия элемента (рис. 5) составив для него уравнение статики :

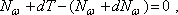
откуда после несложных преобразований, учитывая, что

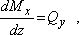
получаем формулу для касательных напряжений при нормальном поперечном изгибе призматического стержня которая называется формулой Журавского.

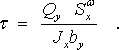
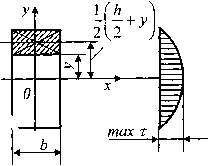
Рис. 6 Распределение касательных напряжений по контуру прямоугольного сечения

В этой формуле b_y — ширина сечения в том месте, где определяются касательные напряжения, а статический момент, подставляемый в эту формулу, может быть вычислен как для верхней, так и для нижней части (статические моменты этих частей сечения относительно его центральной оси Ох отличаются только знаком, так как статическим момент всего сечения равен нулю).

В качестве примера применения формулы Журавского построим эпюру касательных напряжений для случая прямоугольного поперечного сечения балки (рис. 6.). Учитывая, что для этого сечения

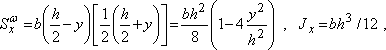
получаем

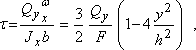
где F=bh—площадь прямоугольника.

Как видно из формулы, касательные напряжения по высоте сечения меняются по закону квадратичеокой параболы, достигая максимума на нейтральной оси

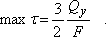
Сделаем несколько замечаний, касающихся расчетов на прочность при прямом поперечном изгибе. В отличие от простых видов деформации, когда в поперечных сечениях стержня возникает лишь один силовой фактор, к которым относятся и изученные выше растяжение (сжатие) и чистый изгиб, прямой поперечный изгиб должен быть отнесен к сложным видам деформации. В поперечных сечениях стержня при поперечном изгибе возникают два силовых фактора: изгибающий момент М_х и поперечная сила Q_y (рис. 7), напряженное состояние является упрощенным плоским, при котором в окрестности произвольно выбранных точек поперечного сечения действуют нормальные и касательные напряжения. Поэтому условие прочности для таких точек должно быть сформулировано на основе какого-либо уже известного критерия прочности.

Однако учитывая, что наибольшие нормальные напряжения возникают в крайних волокнах, где касательные напряжения отсутствуют (рис. 7), а наибольшие касательные напряжения во многих случаях имеют место в нейтральном слое, где нормальные напряжения равны нулю, условия прочности в этих случаях формулируются раздельно по нормальным и касательным напряжениям

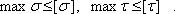
Рис.7 Распределение нормальных и касательных напряжений по контуру сечения

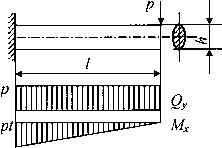
Рис. 8 К сравнительной оценке модулей напряжения

Покажем, что доминирующая роль в расчетах на прочность балки, подвергнутой поперечному изгибу, будет принадлежать расчету по нормальным напряжениям. Для этого оценим порядок max и max на примере консольной балки, показанной на рис. 8:

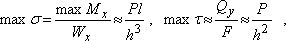
В лекции "8 Методы и средства количественного и качественного учета нефти и нефтепродуктов" также много полезной информации.

так как

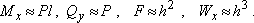
Тогда

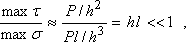
откуда max <<max, а поскольку то доминирующим в этом случае будет расчет по нормальным напряжениям и условие прочности, например, для балки из пластичного материала, работающей на прямой изгиб, как и в случае чистого изгиба будет иметь вид: