Однофакторные производственные функции
Лекция 1. Однофакторные производственные функции
Возможности любого производства отражаются характером зависимости между объемом выпускаемой продукции и соответствующими ему затратами сырья, полуфабрикатов, энергии, капиталовложений, труда и т.д. Всевозможные виды затрат называются факторами производства или ресурсами. Факторы производства имеют различные измерения (тонны, метры, киловатт-часы и др.). Общей единицей измерения всех ресурсов может служить рубль или другая денежная единица. Поэтому удобно иметь дело со стоимостным выражением как факторов производства, так и выпускаемой в результате их использования продукции.
Определение. Функцию, выражающую зависимость между стоимостью выпускаемой продукции и стоимостью суммарных затрат на ее производство, называют однофакторной производственной функцией.
Функция, в которой роль независимой переменной играют затраты, а зависимая переменна определяет уровень выпуска, называется функцией выпуска. В функции затрат, наоборот, независимая переменная- выпуск, а зависимая- затраты.
Пример 1. Если затраты  прямо пропорциональны объему выпуска
прямо пропорциональны объему выпуска  , то функция затрат имеет вид
, то функция затрат имеет вид
 .
.
С помощью однофакторных производственных функций описывается также зависимость объема выпускаемой продукции от затрат некоторого специфического вида ресурса (трудовые ресурсы, основные производственные фонды, объем капиталовложений, различные виды сырья и др.). При этом затраты всех других участвующих в производстве ресурсов считаются постоянными.
Пример 2. С помощью функции вида
Рекомендуемые материалы
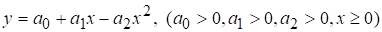
можно охарактеризовать зависимость урожайности  некоторой сельскохозяйственной культуры от количества
некоторой сельскохозяйственной культуры от количества  внесенных удобрений.
внесенных удобрений.
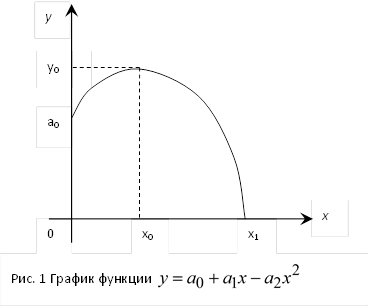
При отсутствии удобрений урожайность составляет  единиц. С увеличением объема используемых удобрений урожай сначала возрастает и при
единиц. С увеличением объема используемых удобрений урожай сначала возрастает и при  достигает наибольшего значения.
достигает наибольшего значения.
Дальнейшее наращивание затрат удобрений оказывается неразумным, так как приводит к снижению урожая и даже полной его потере при  (рис.1).
(рис.1).
 |
Пример 3. Гиперболическая зависимость
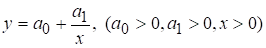
применяется, например, для моделирования зависимости затрат  на единицу выпускаемой продукции от объема производства
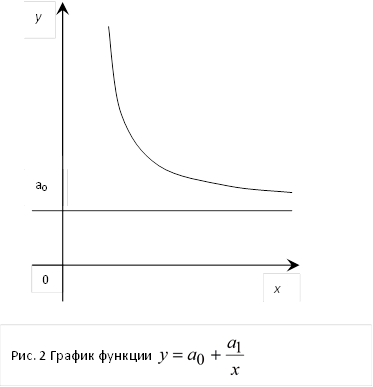
на единицу выпускаемой продукции от объема производства  (рис.2). Величина
(рис.2). Величина  уменьшается с увеличением
уменьшается с увеличением  , это означает, что с увеличением объема производства доля затрат неограниченно убывает.
, это означает, что с увеличением объема производства доля затрат неограниченно убывает.
При большом объеме производства ( ) удельные затраты лишь незначительно отличаются от
) удельные затраты лишь незначительно отличаются от  (
( ).
).
Пример 4. Экспоненциальная производственная функция
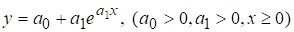
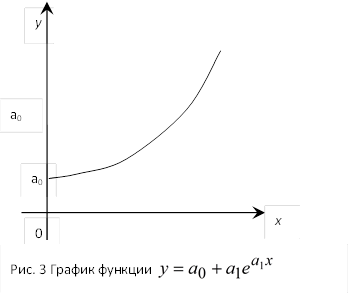
используется, например, для исследования динамики изменения объема производств  с течением времени
с течением времени  (рис.3).
(рис.3).
В начальный момент времени  объем производства
объем производства  . Крутизна кривой на рис. 3 зависит от коэффициентов
. Крутизна кривой на рис. 3 зависит от коэффициентов  .
.
 |
Зависимость  имеет место ив следующей ситуации. Если на банковский счет кладется сумма
имеет место ив следующей ситуации. Если на банковский счет кладется сумма  , то через
, то через  лет на счете будет сумма
лет на счете будет сумма  , если банк выплачивает
, если банк выплачивает  % годовых.
% годовых.
Пример 5. Показательная функция
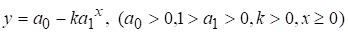
может моделировать влияние затрат переменного ресурса  на выпуск
на выпуск  продукции, если уровень выпуска не может быть больше некоторой предельной величины
продукции, если уровень выпуска не может быть больше некоторой предельной величины  . Так как
. Так как  , то с ростом
, то с ростом 
 неограниченно убывает, а
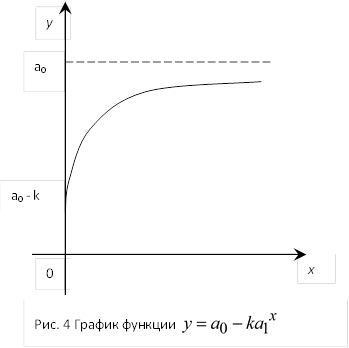
неограниченно убывает, а  возрастает. Если
возрастает. Если  , то
, то  . При
. При  выпуск равен
выпуск равен  (рис.4).
(рис.4).
 |
Пример 6. Степенная производственная функция
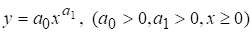
обычно описывает ситуации, в которых рост затрат  некоторого ресурса
некоторого ресурса  ведет к неограниченному увеличению выпуска
ведет к неограниченному увеличению выпуска  . Насколько быстро растет
. Насколько быстро растет  зависит от величины параметров
зависит от величины параметров  (рис. 5).
(рис. 5).
 |
Лекция 2. Экономический смысл производной и некоторых теорем дифференциального исчисления
Пусть функция  выражает количество произведенной продукции
выражает количество произведенной продукции  за время
за время  . Необходимо найти производительность труда в момент времени
. Необходимо найти производительность труда в момент времени  .
.
За период времени от  до
до  количество произведенной продукции изменится от значения
количество произведенной продукции изменится от значения  до значения
до значения  . Тогда средняя производительность труда за этот период времени равна
. Тогда средняя производительность труда за этот период времени равна  . Очевидно, что производительность труда в момент времени
. Очевидно, что производительность труда в момент времени  можно определить как предельное значение средней производительности за период времени от
можно определить как предельное значение средней производительности за период времени от  до
до  при
при  , т.е. равна
, т.е. равна
 .
.
Экономический смысл производной: производительность труда есть производная объема произведенной продукции по времени.
Производная логарифмической функции  называется логарифмической производной, а так же относительной скоростью изменения функции или темпом изменения функции.
называется логарифмической производной, а так же относительной скоростью изменения функции или темпом изменения функции.
Пример 7. Объем продукции  , произведенной бригадой рабочих, может быть описан уравнением
, произведенной бригадой рабочих, может быть описан уравнением  ,
,  , где
, где  - рабочее время в часах. Вычислить производительность труда, скорость и темп ее изменения через час после начала работы и за час до ее окончания.
- рабочее время в часах. Вычислить производительность труда, скорость и темп ее изменения через час после начала работы и за час до ее окончания.
Производительность труда выражается производной
 ,
,
а скорость и темп изменения производительности – соответственно производной  и логарифмической производной
и логарифмической производной 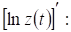
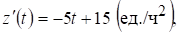
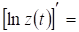
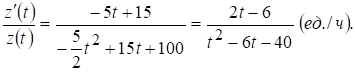
В заданные моменты времени  соответственно имеем:
соответственно имеем: 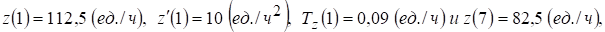
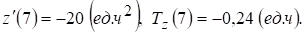
Итак, к концу работы производительность труда существенно снижается; при этом изменение знака  и логарифмической производной с плюса на минус свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется её снижением в последние часы.
и логарифмической производной с плюса на минус свидетельствует о том, что увеличение производительности труда в первые часы рабочего дня сменяется её снижением в последние часы.
Рассмотрим еще одно понятие, иллюстрирующее экономический смысл производной.
Обозначим через  объем производства некоторой продукции, через
объем производства некоторой продукции, через  - суммарные затраты или издержки производства. Производственная функция (функция затрат) описывает зависимость издержек производства
- суммарные затраты или издержки производства. Производственная функция (функция затрат) описывает зависимость издержек производства  от объема
от объема  выпускаемой продукции:
выпускаемой продукции:
 .
.
Если объем производства увеличится на  единиц, то затраты возрастут на
единиц, то затраты возрастут на  единиц.
единиц.
Среднее приращение издержек выражается отношением  .
.
Под предельными издержками производства понимают предел среднего приращения издержек при безграничном уменьшении  , т.е.
, т.е.
 . (1)
. (1)
Предел (1) выражает дополнительные затраты на производство продукции при увеличении объема производства на малую единицу, если исходный объем производства составляет  единиц.
единиц.
Экономический смысл производной в данной точке: производная выражает предельные издержки производства при данном объеме и характеризует приблизительно дополнительные затраты на производство единицы дополнительной продукции.
Пример 8. Допустим, функция затрат имеет вид:
 .
.
Определим предельные издержки производства при данном объеме выпуска  .
.
Решение.  , тогда
, тогда  .
.
Видим, что  и, вообще,
и, вообще,  , если
, если  . То есть с увеличением объема производства предельные издержки (дополнительные затраты на следующую за
. То есть с увеличением объема производства предельные издержки (дополнительные затраты на следующую за  -овой малую единицу выпуска) убывают.
-овой малую единицу выпуска) убывают.
Увеличение выпуска на малую единицу требует все меньших дополнительных затрат.
Пример 9. Пусть зависимость спроса на товар от цены на него выражается формулой  . Определим скорость изменения спроса, когда цена на товар составляет 1 ден.ед., 4 ден. ед.
. Определим скорость изменения спроса, когда цена на товар составляет 1 ден.ед., 4 ден. ед.
Решение. Скорость изменения любой функции равна ее производной. В данном случае
 .
.
Отсюда  .
.
Знак “минус” показывает, что с увеличением цены спрос на товар падает.
Экономический смысл теоремы Ферма
Теорема Ферма. Если дифференцируемая на промежутке  функция
функция  достигает наибольшего или наименьшего значения во внутренней точке
достигает наибольшего или наименьшего значения во внутренней точке  этого промежутка, то производная функции в этой точке равна нулю, т.е.
этого промежутка, то производная функции в этой точке равна нулю, т.е. 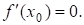
Один из базовых законов теории производства звучит так: оптимальный для производства уровень пуска товара определяется равенством предельных издержек и предельного дохода.
Обозначим функцию прибыли за  . Тогда
. Тогда  , где
, где  - функция дохода,
- функция дохода,  - функция издержек. Очевидно, что оптимальным уровнем производства является тот, при котором прибыль максимальна, т.е. такое значение выпуска
- функция издержек. Очевидно, что оптимальным уровнем производства является тот, при котором прибыль максимальна, т.е. такое значение выпуска  , при котором функция
, при котором функция  имеет экстремум (максимум). По теореме Ферма в этой точке
имеет экстремум (максимум). По теореме Ферма в этой точке  . Но
. Но  , поэтому
, поэтому  , т.е. предельные издержки
, т.е. предельные издержки  и предельный доход
и предельный доход  равны при оптимальном выпуске
равны при оптимальном выпуске  .
.
Другое важное понятие теории производства- это уровень наиболее экономичного производства, при котором средние издержки по производству минимальны. Соответствующий экономический закон гласит: уровень наиболее экономичного производства определяется равенством средних и предельных издержек.
Получим это условие как следствие теоремы Ферма. Средние издержки определяются как  , т.е. издержки по производству товара, деленные на произведенное количество товара. Минимум этой величины достигается в критической точке функции
, т.е. издержки по производству товара, деленные на произведенное количество товара. Минимум этой величины достигается в критической точке функции  , т.е. при условии
, т.е. при условии  , откуда
, откуда  , т.е.
, т.е.  . Что и требовалось доказать.
. Что и требовалось доказать.
Экономический смысл теоремы Лагранжа
Теорема Лагранжа. Если функция  непрерывна на промежутке
непрерывна на промежутке  и дифференцируема в
и дифференцируема в  , то существует по крайней мере одна точка
, то существует по крайней мере одна точка  , такая, что справедливо неравенство:
, такая, что справедливо неравенство:
 .
.
Экономический смысл теоремы Лагранжа. Пусть  описывает зависимость выпуска
описывает зависимость выпуска  от затрат
от затрат  некоторого специфического ресурса. Если объем затрат увеличили с
некоторого специфического ресурса. Если объем затрат увеличили с  до
до  единиц, то разность
единиц, то разность  выражает соответствующее изменение выпуска.
выражает соответствующее изменение выпуска.
Отношение
 (2)
(2)
показывает на сколько единиц в среднем изменяется выпуск продукции, если затраты возросли на одну единицу. Другими словами, (4)- средняя производительность ресурса на промежутке  .
.
Предельная производительность ресурса равна значению производной функции выпуска при данном уровне затрат. Если затраты ресурса  составляют
составляют  единиц, то
единиц, то  - соответствующая им предельная производительность
- соответствующая им предельная производительность  .
.
На основании теоремы Лагранжа можно утверждать, что для процесса производства описываемого функцией выпуска  , которая непрерывна на
, которая непрерывна на  и дифференцируема в
и дифференцируема в  , существует, по крайней мере, один уровень затрат
, существует, по крайней мере, один уровень затрат  , при котором предельная производительность соответствующего ресурса совпадает с его средней производительностью на
, при котором предельная производительность соответствующего ресурса совпадает с его средней производительностью на  .
.
Экономический смысл выпуклости функции
Закон убывающей доходности: с увеличением производства дополнительная продукция, полученная на каждую новую единицу ресурса (трудового, технологического и т.д.), с некоторого момента убывает.
Иными словами, величина  , где
, где  - приращение ресурса, а
- приращение ресурса, а  - приращение выпуска продукции, уменьшается при увеличении
- приращение выпуска продукции, уменьшается при увеличении  . Таким образом, закон убывающей доходности формулируется так: функция
. Таким образом, закон убывающей доходности формулируется так: функция  , выражающая зависимость выпуска продукции от вложенного ресурса, является функцией выпуклой вверх.
, выражающая зависимость выпуска продукции от вложенного ресурса, является функцией выпуклой вверх.
Закон убывающей полезности: с ростом количества товара дополнительная полезность от каждой новой его единицы с некоторого момента убывает.
Функция полезности  , где
, где  - товар,
- товар,  - полезность, есть величина субъективная для каждого отдельного потребителя, но достаточно объективная для общества в целом. Очевидно, закон убывающей полезности можно переформулировать так: функция полезности является функцией выпуклой вверх.
- полезность, есть величина субъективная для каждого отдельного потребителя, но достаточно объективная для общества в целом. Очевидно, закон убывающей полезности можно переформулировать так: функция полезности является функцией выпуклой вверх.
Задания для самостоятельной работы
1. Найдите предельную производительность ресурса (скорость изменения функции), если функция выпуска имеет вид:
Индивидуальная психокоррекция - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
 ,
,
а затраты ресурса составляют: 1) 2 усл.ед., 2) 5 усл.ед.
Определите, начиная с какого момента увеличение затрат данного ресурса становится экономически невыгодным. Приведите примеры экономических ситуаций, которые могут быть описаны с помощью функций выпуска указанного вида.
2. Определите скорость изменения спроса (предельный спрос) при цене в 1 ден.ед.; 3 ден.ед.; 10 ден.ед., если зависимость спроса на товар от цены на него выражается формулой
 .
.
Сравните и объясните результаты.






















