Задачи эконометрики
Власов М. П.
конспект лекций по дисциплине
Компьютерные методы статистического анализа и прогнозирование
ТЕМА 7 Задачи эконометрики
Содержание
стр.
1. Определение эконометрики …………..……………………………… 2
2. Предмет эконометрики ………………………………….……………. 4
3. Метод эконометрики ………………………………………………….. 5
Рекомендуемые материалы
4.Спецификация модели ……………………………………………….. 14
5. Идентифицируемость и идентификация модели ………………….. 15
6. Математико-статистический инструментарий эконометрики ……. 18
Литература ……………………………………………………………… 27
Санкт-Петербург 2008
1. Определение эконометрики
Эконометрика (эконометрия) (от экономики и греч. metreo - измеряю), научная дисциплина, позволяющая на базе положений экономической теории и результатов экономических измерений придавать конкретное количественное выражение общим (качественным) закономерностям, обусловленным экономической теорией. При этом основную роль в математическом оснащении этой дисциплины играют методы математической статистики, и в первую очередь, — многомерного статистического анализа.
Таким образом, суть эконометрики - именно в синтезе экономической теории, экономической статистики и прикладного математического инструментария. Говоря об экономической теории в рамках эконометрики, будем интересоваться не просто выявлением объективно существующих (на качественном уровне) экономических законов и связей между экономическими показателями, но и подходами к их формализации, включающими методы
| Эконометрика | |||||||||||
| Методы: регрессионный анализ; обобщённый метод моментов; системы одновременных уравнений; анализ временных рядов; статистические методы классификации и снижения размерности; нспараметрпческне и полупараметрнческие методы статистического анализа. | Приложения: макроуровень (модели национальной экономики); мезоуровень (модели региональной экономики, отраслей, секторов); микроуровень (модели поведения потребителя, домашних хозяйств, фирм, предприятий). | ||||||||||
| Эконометрическая теория (макро-и микроэкономика, математическая экономика) | Социально-экономическая статистика (включая информационное обеспечение экономических исследований) | Теория вероятностей и математическая статистика | |||||||||
| ИСТОЧНИКИ БАЗОВЫХ КОМПОНЕНТОВ ЭКОНОМЕТРИКИ | |||||||||||
Рис. Эконометрика и её место в ряду других экономических и статистических дисциплин.
спецификации и идентификации соответствующих моделей с учётом решения проблемы их идентифицируемости (эти понятия приведены ниже). При рассмотрении экономической статистики как составной части эконометрики прежде всего нас будет интересовать тот аспект этой самостоятельной дисциплины, который непосредственно связан с информационным обеспечением анализируемой эконометрической модели, хотя в этих рамках специалисту по эконометрике зачастую приходится решать полный спектр соответствующих задач: выбор необходимых экономических показателей и обоснование способа их измерения, определение плана статистического обследования и т. п. Наконец, прикладной математической инструментарий эконометрики в качестве своей основной составляющей содержит ряд специальных разделов многомерного статистического анализа:
· линейные (классическая и обобщённая) и некоторые специальные модели регрессии;
· методы и модели анализа временных рядов;
· обобщённый метод моментов;
· так называемые системы одновременных уравнений;
· статистические методы классификации и снижения размерности анализируемого признакового пространства.
Однако эконометрика использует понятия, постановки и методы решения задач и из многих других разделов математики: теории вероятностей, математического программирования, численных методов решения задач линейной алгебры, систем нелинейных уравнений, теории нахождения неподвижных точек отображений.
Представленная на рисунке схема при всей своей условности и неполноте в целом даёт общее наглядное представление об эконометрике и её месте в ряду других экономических и статистических дисциплин.
Именно «приземление» экономической теории на базу конкретной экономической статистики и извлечение из этого приземления с помощью подходящего математического аппарата вполне определённых количественных взаимосвязей являются ключевыми моментами в понимании сущности эконометрики. Это, в частности, обеспечивает разграничение эконометрики с такими дисциплинами как математическая экономия, описательная экономическая статистика и математическая статистика. Так, математическая экономия, которая часто определяется как математически сформулированная экономическая теория, изучает взаимосвязи между экономическими переменными на общем (неколичественном) уровне. Она преобразуется в эконометрику, когда символически представленные в этих взаимосвязях коэффициенты заменяются конкретными численными оценками, полученными на базе соответствующих экономических данных.
2. Предмет эконометрики
Из определения эконометрики следует, что предметом этой дисциплины являются экономические и социально-экономические приложения, а именно модельное описание конкретных количественных взаимосвязей, существующих между анализируемыми показателями.
К числу типовых экономических моделей, конструируемых и изучаемых с помощью эконометрических методов, относятся:
· производственные функции, выражающие взаимосвязи между затратами и результатами производственной деятельности экономических систем различных уровней;
· модели функционирования национальной экономики;
· типологизация объектов и поведения агентов (стран, регионов, фирм, потребителей);
· целевые функции потребительского предпочтения и функции спроса;
· модели распределительных отношений в обществе;
· модели рынка и экономического равновесия;
· модели интернационализации национальных экономик;
· модели межстранового и межрегионального анализа и др.
При всём разнообразии спектра решаемых с помощью эконометрики задач их, тем не менее, было бы удобно расклассифицировать по трём направлениям:
· по конечным прикладным целям;
· по уровню иерархии;
· по профилю анализируемой экономической системы.
По конечным прикладным целям выделим две основные:
а) прогноз экономических и социально-экономических показателей (переменных), характеризующих состояние и развитие анализируемой системы;
б) имитация различных возможных сценариев социально-экономи-ческого развития анализируемой системы, когда статистически выявленные взаимосвязи между характеристиками производства, потребления, социальной и финансовой политики.
Они используются для прослеживания того, как планируемые (возможные) изменения тех или иных поддающихся управлению параметров производства или распределения скажутся на значениях интересующих нас «выходных» характеристик (в специальной литературе исследования подобного рода называют также сценарным или ситуационным анализом).
По уровню иерархии анализируемой экономической системы выделяются макроуровень (т. е. страны в целом), мезоуровень (регионы, отрасли, корпорации) и микроуровень (семьи, предприятия, фирмы).
В некоторых случаях должен быть определён профиль эконометрического моделирования: исследование может быть сконцентрировано на проблемах рынка, инвестиционной, финансовой или социальной политики, ценообразования, распределительных отношений, спроса и потребления, или на определённом комплексе проблем. Однако чем претенциознее по широте охвата анализируемых проблем эконометрнческое исследование, тем меньше шансов провести его достаточно эффективно.
3. Метод эконометрики
В общей формулировке эконометрический метод может быть описан следующим образом. Постулируется, что анализируемые переменные (экономические показатели)  являются случайными величинами, совместный закон распределения вероятностей (з. р. в.) которых не известен исследователю, но принадлежит некоторому семейству функций. В процессе функционирования анализируемой экономической системы генерируются наблюдаемые значения
являются случайными величинами, совместный закон распределения вероятностей (з. р. в.) которых не известен исследователю, но принадлежит некоторому семейству функций. В процессе функционирования анализируемой экономической системы генерируются наблюдаемые значения  (
( ) интересующих исследователя переменных. Идентификация модели (анализируемой системы) заключается в выборе из упомянутого семейства конкретного закон распределения вероятностей, наиболее хорошо (в определённом смысле) согласующегося с имеющимися в распоряжении исследователя сгенерированными системой данными. Различные спецификации (конкретизации, основанные на дополнительных исходных допущениях) этой общей постановки проблемы и приводят к широкому спектру методов и моделей эконометрического анализа: регрессии, временным рядам, системам одновременных уравнений и другим методам, используемым при решении задач экономического прогноза, ситуационного анализа, оценивания важных экономических характеристик.
) интересующих исследователя переменных. Идентификация модели (анализируемой системы) заключается в выборе из упомянутого семейства конкретного закон распределения вероятностей, наиболее хорошо (в определённом смысле) согласующегося с имеющимися в распоряжении исследователя сгенерированными системой данными. Различные спецификации (конкретизации, основанные на дополнительных исходных допущениях) этой общей постановки проблемы и приводят к широкому спектру методов и моделей эконометрического анализа: регрессии, временным рядам, системам одновременных уравнений и другим методам, используемым при решении задач экономического прогноза, ситуационного анализа, оценивания важных экономических характеристик.
Все эконометрические модели, независимо от того, относятся они ко всему хозяйству или к его элементам (т. е. к макроэкономике, отрасли, фирме или рынку), имеют некоторые общие особенности. Во-первых, они основаны на предположении, что поведение экономических переменных определяется с помощью совместных и одновременных операций с некоторым числом экономических соотношений. Во-вторых, принимается гипотеза, в силу которой модель, допуская упрощение сложной действительности, тем не менее, улавливает главные характеристики изучаемого объекта. В-третьих, создатель модели полагает, что на основе достигнутого с её помощью понимания реальной системы удастся предсказать её будущее движение и, возможно, управлять им в целях улучшения экономического благосостояния.
Пример. Предположим, что экономическая теория позволяет сформулировать следующие положения:
· потребление есть возрастающая функция от имеющегося в наличии дохода, но возрастающая, видимо, медленнее, чем рост дохода;
· объём инвестиций есть возрастающая функция национального дохода и убывающая функция некоторых характеристик государственного регулирования (например, нормы процента);
· национальный доход есть сумма потребительских, инвестиционных и государственных закупок товаров и услуг.
Первая задача - перевести эти положения на математический язык. Здесь открывается многообразие возможных решений, удовлетворяющих сформулированным априорным требованиям теории. Какие соотношения выбрать между переменными - линейные или нелинейные? Если остановиться на нелинейных, то какими они должны быть — логарифмическими, полиномиальными или какими-либо ещё? Даже после определения формы конкретного соотношения, остаётся ещё нерешённой проблема выбора для различных уравнений запаздываний по времени. Будут ли, например, инвестиции текущего периода реагировать только на национальный доход, произведённый в последнем периоде, или же на них скажется динамика нескольких предыдущих периодов? Обычный выход из этих трудностей состоит в выборе при первоначальном анализе наиболее простой из возможных форм этих соотношений. Тогда появляется возможность записать на основе указанных выше положений следующую линейную относительно анализируемых переменных и аддитивную относительно случайных составляющих модель:
 , (3.1.)
, (3.1.)
 , (3.2.)
, (3.2.)
 , (3.3.)
, (3.3.)
где априорные ограничения выражены неравенствами
 ;
;  ;
;  .
.
Эти три соотношения вместе с ограничениями образуют модель. В ней  обозначает потребление,
обозначает потребление,  - инвестиции,
- инвестиции,  - национальный доход,
- национальный доход,  - подоходный налог,
- подоходный налог,  -норму процента как инструмент государственного регулирования,
-норму процента как инструмент государственного регулирования,  - государственные закупки товаров и услуг, измеренные в «момент времени»
- государственные закупки товаров и услуг, измеренные в «момент времени»  .
.
Присутствие в уравнениях (3.1.) и (3.2.) «остаточных» случайных составляющих  и
и  обусловлено необходимостью учесть влияние соответственно на (
обусловлено необходимостью учесть влияние соответственно на ( ) и (
) и ( ) ряда неучтённых факторов. Действительно, нереалистично ожидать, что величина потребления (
) ряда неучтённых факторов. Действительно, нереалистично ожидать, что величина потребления ( ) будет однозначно определяться уровнями национального дохода (
) будет однозначно определяться уровнями национального дохода ( ) и подоходного налога (
) и подоходного налога ( ); аналогично величина инвестиций (
); аналогично величина инвестиций ( ) зависит, очевидно, не только от достигнутого в предыдущий год уровня национального дохода (
) зависит, очевидно, не только от достигнутого в предыдущий год уровня национального дохода ( ) и от величины нормы процента (
) и от величины нормы процента ( ) , но и от ряда не учтённых в уравнении (3.2.) факторов.
) , но и от ряда не учтённых в уравнении (3.2.) факторов.
Полученная модель содержит два уравнения, объясняющих поведение потребителей и инвесторов, и одно тождество. Мы сформулировали её для дискретных периодов времени и выбрали запаздывание (лаг) в один период для отражения воздействия национального дохода на инвестиции.
В дальнейшем этот пример используется для пояснения ряда основных понятий эконометрического моделирования.
Основные понятия эконометрического моделирования. В любой эконометрической модели в зависимости от конечных прикладных целей её использования все участвующие в ней переменные подразделяются на:
· экзогенные, т. е. задаваемые как бы «извне», автономно, в определённой степени управляемые (планируемые);
· эндогенные, т. е. такие переменные, значения которых формируются в процессе и внутри функционирования анализируемой социально-экономической системы в существенной мере под воздействием экзогенных переменных и, конечно, во взаимодействии друг с другом; в эконометрической модели они являются предметом объяснения;
· предопределённые, т. е. выступающие в системе в роли факторов-аргументов, или объясняющих переменных.
Множество предопределённых переменных формируется из всех экзогенных переменных (которые могут быть «привязаны» к прошлым, текущему или будущим моментам времени) и так называемых лаговых эндогенных переменных, т. е. таких эндогенных переменных, значения которых входят в уравнения анализируемой эконометрической системы измеренными в прошлые (по отношению к текущему) моменты времени, а, следовательно, являются уже известными, заданными.
Набор взаимосвязанных регрессионных уравнений, в которых одни и те же переменные могут одновременно играть роль (в различных уравнениях системы) результирующих показателей и объясняющих переменных (предикторов) называют системой одновременных уравнений (СОУ). Очевидно модель (3.1.)-(3.3.) представляет собой пример СОУ. В данном примере потребление ( ) , инвестиции (
) , инвестиции ( ) и национальный доход (
) и национальный доход ( ) в текущий момент времени
) в текущий момент времени  являются эндогенными переменными; подоходный налог (
являются эндогенными переменными; подоходный налог ( ), норма процента как инструмент государственного регулирования (
), норма процента как инструмент государственного регулирования ( ) и государственные закупки товаров и услуг (
) и государственные закупки товаров и услуг ( ) - экзогенные переменные, которые вместе с национальным доходом в предшествующий момент времени (
) - экзогенные переменные, которые вместе с национальным доходом в предшествующий момент времени ( ) образуют множество предопределённых переменных.
) образуют множество предопределённых переменных.
Таким образом, можно сказать, что эконометрическая модель служит для объяснения поведения эндогенных переменных в зависимости от значений экзогенных и лаговых эндогенных переменных.
При построении и анализе эконометрической модели следует различать её структурную и приведённую формы. Для пояснения этих понятий условимся в дальнейшем обозначать латинской буквой  вектор-столбец всех предопределённых переменных (он включает в себя все экзогенные переменные и все участвующие в модели лаговые эндогенные переменные). Пусть общее число эндогенных переменных равно
вектор-столбец всех предопределённых переменных (он включает в себя все экзогенные переменные и все участвующие в модели лаговые эндогенные переменные). Пусть общее число эндогенных переменных равно  , а общее число предопределённых переменных —
, а общее число предопределённых переменных —  . Общее число уравнений и тождеств в эконометрической модели равно числу эндогенных переменных, т. е. равно
. Общее число уравнений и тождеств в эконометрической модели равно числу эндогенных переменных, т. е. равно  . И пусть из общего числа от соотношений модели имеется
. И пусть из общего числа от соотношений модели имеется  уравнений, включающих случайные остаточные компоненты, и
уравнений, включающих случайные остаточные компоненты, и  тождеств (
тождеств ( ). Разобьём вектор эндогенных переменных
). Разобьём вектор эндогенных переменных  на два подвектора
на два подвектора  и
и  , при этом порядок, в котором перенумерованы эндогенные переменные, не имеет значения.
, при этом порядок, в котором перенумерованы эндогенные переменные, не имеет значения.
Тогда общий вид линейной эконометрической модели может быть представлен в форме
 (3.4.)
(3.4.)
где  — матрица размерности (
— матрица размерности ( ) из коэффициентов при
) из коэффициентов при  в
в  первых уравнениях;
первых уравнениях;
 - матрица из коэффициентов при
- матрица из коэффициентов при  в
в  первых уравнениях;
первых уравнениях;
 - вектор-столбец предопределённых переменных (в нём
- вектор-столбец предопределённых переменных (в нём  );
);
 — матрица размерности
— матрица размерности  из коэффициентов при предопределённых переменных в первых
из коэффициентов при предопределённых переменных в первых  уравнениях (очевидно, коэффициенты
уравнениях (очевидно, коэффициенты  играют роль свободных членов уравнений);
играют роль свободных членов уравнений);
 - матрица размерности
- матрица размерности  из коэффициентов при
из коэффициентов при  в
в  тождествах системы;
тождествах системы;
 - матрица размерности
- матрица размерности  из коэффициентов при
из коэффициентов при  в
в  тождествах системы;
тождествах системы;
 - матрица размерности
- матрица размерности  из коэффициентов при предопределённых переменных в
из коэффициентов при предопределённых переменных в  тождествах системы;
тождествах системы;
 -вектор-столбец размерности
-вектор-столбец размерности  случайных остаточных составляющих
случайных остаточных составляющих  первых уравнений системы;
первых уравнений системы;
 - вектор-столбец размерности
- вектор-столбец размерности  состоящий из нулей.
состоящий из нулей.
Заметим, что исходными статистическими данными, необходимыми для проведения статистического анализа системы (3.4.) (а именно, для оценки неизвестных коэффициентов  и
и  проверки статистических гипотез, например, о линейном характере исследуемых зависимостей и т. п.), являются матрицы
проверки статистических гипотез, например, о линейном характере исследуемых зависимостей и т. п.), являются матрицы
 и
и  (3.5.)
(3.5.)
соответственно размерностей  и
и  , а все элементы матриц В3, В4 и С2 являются известными (их числовые значения определяются содержательным смыслом соответствующих тождеств системы).
, а все элементы матриц В3, В4 и С2 являются известными (их числовые значения определяются содержательным смыслом соответствующих тождеств системы).
Система (3.4) может быть записана также в виде
 ,
,  (3.4’)
(3.4’)
или в виде
 , (3.4")
, (3.4")
где
 ,
,  ,
,  ,
,  ,
,  ,
,
а матрицы У и X определены в (3.5.).
Система уравнений и тождеств вида (3.4.) (или эквивалентных ей записей (3.4') или (3.4")) называется структурной формой линейной эконометрической модели. При этом предполагается, что коэффициент при эндогенной переменной  в структурном стохастическом уравнении
в структурном стохастическом уравнении  (
( ) равен единице (правило нормировки системы), а матрицы
) равен единице (правило нормировки системы), а матрицы  и
и  невырождены (допускаются и другие способы нормировки системы).
невырождены (допускаются и другие способы нормировки системы).
Поскольку при реализации конечных прикладных целей эко-нометрического моделирования (т. е. при прогнозе значений эндогенных переменных и при различных имитационных расчётах) главный интерес представляют соотношения, позволяющие явно выразить все эндогенные переменные  через предопределённые
через предопределённые  , то одновременно со структурной формой имеет смысл рассмотреть так называемую приведённую (редуцированную) форму линейной эконометрической модели. Требуемый результат мы получим, домножив слева обе части соотношений (3.4') на матрицу
, то одновременно со структурной формой имеет смысл рассмотреть так называемую приведённую (редуцированную) форму линейной эконометрической модели. Требуемый результат мы получим, домножив слева обе части соотношений (3.4') на матрицу  и уединив затем
и уединив затем  :
:
 ,
,  , (3.6.)
, (3.6.)
или
 ,
,  (3.6’.)
(3.6’.)
где  матрица
матрица  и вектор остаточных случайных составляющих
и вектор остаточных случайных составляющих  определяются соотношениями
определяются соотношениями
 , (3.7.)
, (3.7.)
 , (3.8.)
, (3.8.)
Система соотношений (3.6’), в которой все эндогенные переменные эконометрической модели явно линейно выражены через предопределённые переменные и случайные остаточные компоненты, называется приведённой формой линейной эконометрической модели.
Проиллюстрируем введённые понятия на примере (3.1)-(3.3).
В этом примере число эндогенных переменных, так же как и общее число всех соотношений модели, равно трём ( ). Среди этих соотношений мы имеем одно тождество (следовательно,
). Среди этих соотношений мы имеем одно тождество (следовательно,  ,
,  ). Общее число предопределённых переменных
). Общее число предопределённых переменных  , в том числе три экзогенные переменные (
, в том числе три экзогенные переменные ( ) и одна лаговая эндогенная переменная (
) и одна лаговая эндогенная переменная ( ) , которую в соответствии с принятой договорённостью кодируем как
) , которую в соответствии с принятой договорённостью кодируем как  (т. е.
(т. е.  ).
).
Структурная форма модели в данном примере задаётся соотношениями (3.1)-(3.3). В общих матричных обозначениях, использованных в (3.4), имеем:
 ,
,  ,
,  ,
,
 ,
,  ,
, 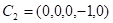
и
 .
.
Если же структурная форма записана в виде (3.4’), то в данном примере участвующие в этой записи матрицы конкретизируются в виде
 ;
;  .
.
и
 .
.
Отметим, что, во-первых, выполнено условие нормировки ( входит в уравнение
входит в уравнение  системы, i = 1,2, с коэффициентом единица); во-вторых, значения элементов матриц В3, В4 и С2 известны, они определяются содержательным смыслом тождества; в третьих, требование невырожденности матриц В4 и В соблюдено; и, наконец, в четвёртых, матрицы
системы, i = 1,2, с коэффициентом единица); во-вторых, значения элементов матриц В3, В4 и С2 известны, они определяются содержательным смыслом тождества; в третьих, требование невырожденности матриц В4 и В соблюдено; и, наконец, в четвёртых, матрицы  и
и  относительно «слабо заполнены» неизвестными (подлежащими статистическому оцениванию) коэффициентами: их всего четыре
относительно «слабо заполнены» неизвестными (подлежащими статистическому оцениванию) коэффициентами: их всего четыре  и
и  . Последняя особенность рассматриваемой эконометрической модели является достаточно общей отличительной чертой систем эконометрических уравнений. Если бы это было не так, т. е. если бы мы были вынуждены иметь дело с системами, «сильно заполненными» неизвестными коэффициентами, то задача статистического анализа таких систем оказывалась бы принципиально неразрешимой: имеющихся исходных статистических данных просто не хватало бы для корректного проведения такого анализа. Ведь при построении и анализе систем эконометрических уравнений, описывающих макроэкономические модели, исследователю зачастую приходится иметь дело с десятками и сотнями эндогенных и экзогенных переменных!
. Последняя особенность рассматриваемой эконометрической модели является достаточно общей отличительной чертой систем эконометрических уравнений. Если бы это было не так, т. е. если бы мы были вынуждены иметь дело с системами, «сильно заполненными» неизвестными коэффициентами, то задача статистического анализа таких систем оказывалась бы принципиально неразрешимой: имеющихся исходных статистических данных просто не хватало бы для корректного проведения такого анализа. Ведь при построении и анализе систем эконометрических уравнений, описывающих макроэкономические модели, исследователю зачастую приходится иметь дело с десятками и сотнями эндогенных и экзогенных переменных!
Приведённая форма модели (3.1)-(3.3) в данном примере имеет вид
 ,
,
 ,
,
 .
.
4.Спецификация модели
Эта проблема включает в себя:
а) определение конечных целей моделирования (прогноз, имитация различных сценариев социально-экономического развития анализируемой системы, оценка определённых экономических характеристик);
б) определение списка экзогенных и эндогенных переменных;
в) определение состава анализируемой системы уравнений и тождеств, их структуры и соответственно списка предопределённых переменных;
г) способ параметризации модели, т. е. определение общего вида искомых функциональных зависимостей, связывающих между собой анализируемые переменные;
д) формулировку исходных предпосылок и априорных ограничений относительно:
• стохастической природы остатков  (в классических вариантах моделей постулируются их взаимная статистическая независимость или некоррелированность, нулевые значения их средних величин и, иногда, сохранение постоянными в процессе наблюдения значений их дисперсий - гомоскедастичность);
(в классических вариантах моделей постулируются их взаимная статистическая независимость или некоррелированность, нулевые значения их средних величин и, иногда, сохранение постоянными в процессе наблюдения значений их дисперсий - гомоскедастичность);
• числовых значений отдельных параметров модели.
Итак, спецификация модели - это первый и, быть может, важнейший шаг эконометрического исследования. От того, насколько удачно решена проблема спецификации и, в частности, насколько реалистичны наши решения и предположения относительно состава эндогенных, экзогенных и предопределённых переменных, структуры и общего вида самой системы уравнений и тождеств, стохастической природы случайных остатков и конкретных числовых значений части неизвестных параметров модели, решающим образом зависит успех всего эконометрического исследования.
Спецификация опирается как на имеющиеся экономические теории, специальные знания или интуитивные представления исследователя об анализируемой экономической системе, так и на специальные методы и приёмы (в том числе, математико-статистические) так называемого разведочного анализа.
5. Идентифицируемость и идентификация модели
При анализе эконометрической модели, представленной системой уравнений вида (3.4) (или (3.4')), исследователя в конечном счёте интересует, прежде всего, поведение эндогенных переменных  . Из соответствующей приведённой формы модели (3.6) видно, что эндогенные переменные
. Из соответствующей приведённой формы модели (3.6) видно, что эндогенные переменные  являются по своей природе случайными величинами, поведение которых определяется внутренней структурой модели, а именно элементами матриц В и С и природой случайных остатков
являются по своей природе случайными величинами, поведение которых определяется внутренней структурой модели, а именно элементами матриц В и С и природой случайных остатков  . Возникает вопрос: а возможно ли, следуя в «обратном направлении», восстановить структурную форму (3.4’) (т. е. все элементы матриц В и С), располагая знанием значений коэффициентов приведённой формы (3.6) (т. е. знанием числовых значений всех элементов матрицы
. Возникает вопрос: а возможно ли, следуя в «обратном направлении», восстановить структурную форму (3.4’) (т. е. все элементы матриц В и С), располагая знанием значений коэффициентов приведённой формы (3.6) (т. е. знанием числовых значений всех элементов матрицы  и природы случайных остатков
и природы случайных остатков  )? Именно этот вопрос и отражает сущность проблемы идентифицируемости эконометрической модели (не смешивать с проблемой идентификации модели, заключающейся в выборе и реализации методов статистического оценивания её неизвестных параметров, см. ниже).
)? Именно этот вопрос и отражает сущность проблемы идентифицируемости эконометрической модели (не смешивать с проблемой идентификации модели, заключающейся в выборе и реализации методов статистического оценивания её неизвестных параметров, см. ниже).
Ответ на поставленный вопрос в общем случае, очевидно, отрицательный: без дополнительных ограничений на внутреннюю структуру модели (т. е. без соблюдения некоторых условий идентифицируемости) по  элементам матрицы
элементам матрицы  невозможно восстановить гораздо большее число элементов матриц В и С (нетрудно подсчитать, что общее число коэффициентов
невозможно восстановить гораздо большее число элементов матриц В и С (нетрудно подсчитать, что общее число коэффициентов  и
и  в структурной форме равно
в структурной форме равно  , хотя, конечно, общее число коэффициентов, подлежащих статистическому оцениванию, оказывается меньшим).
, хотя, конечно, общее число коэффициентов, подлежащих статистическому оцениванию, оказывается меньшим).
В эконометрической теории приняты следующие определения, связанные с проблемой идентифицируемости СОУ.
1) Уравнение структурной формы эконометрической модели называется точно идентифицируемым, если все участвующие в нём неизвестные (т. е. априори не заданные) коэффициенты однозначно восстанавливаются по коэффициентам приведённой формы без каких-либо ограничений на значения последних.
2) Эконометрическая модель называется точно идентифицируемой, если все уравнения сё структурной формы являются точно идентифицируемыми.
3) Уравнение структурной формы называется сверхидентифицируемым, если все участвующие в нём неизвестные коэффициенты восстанавливаются по коэффициентам приведённой формы, причем некоторые из его коэффициентов могут принимать одновременно несколько (более одного) числовых значений, соответствующих одной и той же приведённой форме.
4) Уравнение структурной формы называется неидентифицируемым, если хотя бы один из участвующих в нём неизвестных коэффициентов не может быть восстановлен по коэффициентам приведённой формы. Соответственно модель называется неидентифицируемой, если хотя бы один из коэффициентов структурной формы является неидентифицируемым.
Говоря о проблеме идентифицируемости модели, мы начали с того, что исследователя в конечном счёте интересует поведение эндогенных переменных, и с этой точки зрения может показаться несущественной, более того, надуманной проблема «однозначного возврата» от приведённой формы к структурной. Однако в действительности исследователя могут интересовать оценочные значения коэффициентов именно структурной формы как имеющие прозрачную экономическую интерпретацию (различные эластичности, мультипликаторы и т. п.). Именно поэтому проблема идентифицируемости крайне важна с позиций выработки предложений по решению следующей проблемы - проблемы идентификации эконометрической модели, т. е. проблемы выбора и реализации методов статистического оценивания участвующих в ней неизвестных параметров.
Идентификация. Решение этой проблемы предусматривает «настройку» записанной в общей структурной форме (3.4') модели на реальные статистические данные (3.5). Другими словами, речь идёт о выборе и реализации методов статистического оценивания неизвестных параметров модели (3.4) (т. е. той части элементов матриц В и С, значения которых не являются априори известными) по исходным статистическим данным (3.5).
Верификация модели. Эта проблема, так же, как и проблема идентификации, является специфичной, связанной с построением именно эконометрической модели. Собственно построение эконометрической модели завершается сё идентификацией, т. е. статистическим оцениванием участвующих в ней неизвестных коэффициентов (параметров)  и
и  . После этого, однако, возникают вопросы:
. После этого, однако, возникают вопросы:
а) насколько удачно удалось решить проблемы спецификации, идентифицируемости и идентификации модели, т. е. можно ли рассчитывать на то, что использование построенной модели в целях прогноза эндогенных переменных и имитационных расчётов, определяющих варианты социально-экономического развития анализируемой системы, даст результаты, достаточно адекватные реальной действительности?
б) какова точность (абсолютная, относительная) прогнозных и имитационных расчётов, основанных на построенной модели?
Получение ответов на эти вопросы с помощью тех или иных математико-статистических методов и составляет содержание проблемы верификации эконометрической модели.
6. Математико-статистический инструментарий эконометрики
Математико-статистический инструментарий эконометрики базируется, в основном, на избранных разделах многомерного статистического анализа и анализа временных рядов, развитых в направлении обобщений ряда традиционных для этих разделов постановок задач. Эти обобщения (подчас весьма далеко идущие) инициированы специфическими особенностями экономических приложений.
1) Регрессионный анализ. В это понятие в эконометрике вкладывается широкий смысл. Оно включает в себя, в частности,:
· классическую линейную модель множественной регрессии (КЛММР) и связанный с ней метод наименьших квадратов (МНК);
· обобщённую линейную модель множественной регрессии (ОЛММР) и связанный с ней обобщённый метод наименьших квадратов (ОМНК);
· регрессию со стохастическими объясняющими переменными и связанный с ней метод инструментальных переменных.
В рамках этого же раздела рассматриваются задачи построения регрессионной модели по неоднородным исходным данным (в связи с этим вводится понятие фиктивных переменных либо, если граница между однородными подвыборками исходных данных не определена, предлагается предварительно проводить их кластер-анализ), а также - по цензурированным или урезанным исходным данным (в связи с этим рассматриваются различные модели, учитывающие смещения статистических выводов, вызванные ограничениями на отбор элементов выборки) - тобит-модель, sample selection model.
Цензурирование или урезание результатов выборочного обследования естественным образом возникает при исследовании «длительности жизни» какого-либо процесса или элемента, времени нахождения системы (элемента) в определённом состоянии: время жизни индивида, период безотказной работы прибора, время поиска работы безработным, длительность забастовки и т. п. Модели, описывающие механизм подобных явлений, называют моделями длительности жизни. Центральным объектом исследования в подобных моделях является так называемая интенсивность отказов или коэффициент смертности  , имеющий следующий смысл: если к моменту времени t процесс ещё не завершился (индивид не умер), то вероятность его окончания (смерти) в течение следующего малого промежутка времени
, имеющий следующий смысл: если к моменту времени t процесс ещё не завершился (индивид не умер), то вероятность его окончания (смерти) в течение следующего малого промежутка времени  есть
есть  . В эконометрических исследованиях, как правило, пытаются описать, как интенсивность отказов
. В эконометрических исследованиях, как правило, пытаются описать, как интенсивность отказов  зависит от ряда экзогенных (объясняющих) переменных
зависит от ряда экзогенных (объясняющих) переменных  (например, в демографии исследуют зависимость коэффициента смертности от ряда социально-экономических характеристик индивида). В этом смысле эконометрические модели длительности жизни можно условно также отнести к разделу «Регрессионный анализ».
(например, в демографии исследуют зависимость коэффициента смертности от ряда социально-экономических характеристик индивида). В этом смысле эконометрические модели длительности жизни можно условно также отнести к разделу «Регрессионный анализ».
К этому же разделу относятся и регрессионные модели, в которых зависимая переменная имеет неколичественную природу, — так называемые модели бинарного и множественного выбора (в том числе, логит- и пробит-модели). Граничное положение (между разделами «Регрессионный анализ» и «Анализ временных рядов») занимают регрессионные модели с распределёнными лагами: постановка задачи здесь регрессионная, а исходные данные представлены в виде временных рядов.
2) Анализ временных рядов. Существенную роль в инструментарии эконометрики играют модели авторегрессии порядка  АР(
АР( ), скользящего среднего порядка
), скользящего среднего порядка  CC(
CC( ), авторегрессии - скользящего среднего APCC(
), авторегрессии - скользящего среднего APCC( ), авторегрессии - проинтегрированного скользящего среднего APTlCC(
), авторегрессии - проинтегрированного скользящего среднего APTlCC( ), наконец, различные версии их многомерных обобщений (например, векторные модели авторегрессин ВАР(
), наконец, различные версии их многомерных обобщений (например, векторные модели авторегрессин ВАР( ), векторные модели авторегрессии -скользящего среднего ВАРСС(
), векторные модели авторегрессии -скользящего среднего ВАРСС( ) и др.[1].).
) и др.[1].).
В ряде прикладных эконометрических работ, в частности, при анализе и моделировании макроэкономических данных, характеризующих процессы инфляции и внешней торговли, механизм формирования нормы процента и т. п., была выявлена некоторая общая закономерность в поведении случайных остатков (ошибок прогноза)  исследуемых моделей: их малые и большие значения группировались целыми кластерами, или сериями. Причём это не приводило к нарушению их стационарности и, в частности, их гомоскедастичности для относительно больших временных интервалов, т. е. гипотеза
исследуемых моделей: их малые и большие значения группировались целыми кластерами, или сериями. Причём это не приводило к нарушению их стационарности и, в частности, их гомоскедастичности для относительно больших временных интервалов, т. е. гипотеза  не противоречила имеющимся экспериментальным данным. Однако в рамках моделей АРСС удовлетворительно объяснить этот феномен не удавалось. Требовалась определённая модификация известных моделей.
не противоречила имеющимся экспериментальным данным. Однако в рамках моделей АРСС удовлетворительно объяснить этот феномен не удавалось. Требовалась определённая модификация известных моделей.
Такая модификация была предложена впервые Р. Энглом в 1982. Он рассматривал остатки  как условно гетероскедастичные, связанные друг с другом простейшей авторегрессионной зависимостью, а именно:
как условно гетероскедастичные, связанные друг с другом простейшей авторегрессионной зависимостью, а именно:
 , (6.1.)
, (6.1.)
или, что то же,
 ,
,
где последовательность  , t= 1,2,..., - образует стандартизованный нормальный белый шум (т. е.
, t= 1,2,..., - образует стандартизованный нормальный белый шум (т. е.  и
и  независимы при
независимы при  и
и  , а параметры
, а параметры  и
и  должны удовлетворять ограничениям, обеспечивающим безусловную гомоскедастичность
должны удовлетворять ограничениям, обеспечивающим безусловную гомоскедастичность  (такими ограничениями являются требования
(такими ограничениями являются требования  ,
,  ). При этом под [
). При этом под [ ] подразумевается, что речь идёт о случайной величине, рассматриваемой в предположении, что её значение в предшествующий момент времени зафиксировано (задано). Соответственно, её поведение будет описываться условным законом распределения вероятностей.
] подразумевается, что речь идёт о случайной величине, рассматриваемой в предположении, что её значение в предшествующий момент времени зафиксировано (задано). Соответственно, её поведение будет описываться условным законом распределения вероятностей.
В соответствии с установившейся терминологией, модель (6.1.) называется авторегрессионной условно гетероскедастичной (сокращённо АРУГ). В англоязычной литературе такие модели называют AutoRegressive Conditional Heteroscedasticity (сокращённо ARCH-model).
Использование такой модели для описания поведения остатков моделей регрессии и временных рядов в упомянутых выше типовых ситуациях оказывается более адекватным действительности и позволяет строить более эффективные оценки параметров рассматриваемых моделей, чем обычные или даже обобщённые МНК – оценки.
Естественное обобщение моделей типа (6.1.) было предложено Р. Энглом и Д. Крафтом в 1983:
 , (6.2.)
, (6.2.)
а параметры  связаны некоторыми ограничениями, обеспечивающими безусловную гомоскедастичность остатков
связаны некоторыми ограничениями, обеспечивающими безусловную гомоскедастичность остатков  .
.
Модели (6.2.) называются моделями АРУГ порядка  (сокращённо АРУГ(
(сокращённо АРУГ( )). Содержательно переход к
)). Содержательно переход к  > 1 в моделях (6.2.) означает, что процесс формирования значений остатков
> 1 в моделях (6.2.) означает, что процесс формирования значений остатков  имеет «более длинную память» о величинах предшествующих остатков
имеет «более длинную память» о величинах предшествующих остатков  . Кстати, АРУГ(
. Кстати, АРУГ( )-модель (6.2.) может рассматриваться как некая специальная форма СС(
)-модель (6.2.) может рассматриваться как некая специальная форма СС( )-модели, что и используется при её анализе.
)-модели, что и используется при её анализе.
Дальнейшее обобщение моделей этого типа было сделано в 1986 Т. Боллерслевом. Он предложил описывать поведение остатков  с помощью обобщённой авторегрессионной условно гетероскедастичной модели (ОАРУГ-модели, или, в англоязычном варианте, — GARCH-model), которая записывается в виде
с помощью обобщённой авторегрессионной условно гетероскедастичной модели (ОАРУГ-модели, или, в англоязычном варианте, — GARCH-model), которая записывается в виде
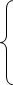
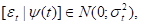
где условная дисперсия  имеет вид (6.3.)
имеет вид (6.3.)
 .
.
В соотношениях (6.3.) под  подразумевается вся информация о процессе
подразумевается вся информация о процессе  , которой мы располагаем к моменту времени
, которой мы располагаем к моменту времени  (т. е. все значения
(т. е. все значения  и
и  для
для  ), а параметры
), а параметры  и
и  (k= 1,2,...,р; j = 0,1,...,q) связаны ограничениями, обеспечивающими безусловную гомоскедастичность остатков
(k= 1,2,...,р; j = 0,1,...,q) связаны ограничениями, обеспечивающими безусловную гомоскедастичность остатков  . Модель ОАРУГ(
. Модель ОАРУГ( ), задаваемая соотношениям (6.3.), может интерпретироваться как специальная форма АРСС(
), задаваемая соотношениям (6.3.), может интерпретироваться как специальная форма АРСС( )-модели. На ряде примеров показано, что использование ОАРУГ(
)-модели. На ряде примеров показано, что использование ОАРУГ( )-модели позволяет добиваться более экономной параметризации в описании поведения остатков
)-модели позволяет добиваться более экономной параметризации в описании поведения остатков  , чем в рамках АРУГ(
, чем в рамках АРУГ( )-моделей (т. е. модели ОАРУГ(
)-моделей (т. е. модели ОАРУГ( ) при малых значениях
) при малых значениях  оказываются более точными, чем АРУГ(
оказываются более точными, чем АРУГ( )-модели при больших значениях
)-модели при больших значениях  ).
).
Другие важные понятия, используемые при анализе временных рядов, это интегрируемость ряда (определённого порядка) и контеграция временных рядов. Одними из первых эти понятия рассмотрели Энгл и К. Грэнжер в связи с задачей построения модели регрессии по нестационарным временным рядам. Временной ряд  называется интегрируемым порядка
называется интегрируемым порядка  , если он становится впервые стационарным после
, если он становится впервые стационарным после  -кратного применения к нему разностного оператора
-кратного применения к нему разностного оператора  . В регрессионном анализе обычно одновременно рассматривается несколько временных рядов. Очевидно, если
. В регрессионном анализе обычно одновременно рассматривается несколько временных рядов. Очевидно, если  - интегрируемый временной ряд порядка
- интегрируемый временной ряд порядка  , и
, и  — интегрируемый временной ряд порядка
— интегрируемый временной ряд порядка  , причём
, причём  , то при любом значении параметра
, то при любом значении параметра  (в том числе при
(в том числе при  , где
, где  - МНК-оценка коэффициента регрессии в модели парной регрессии
- МНК-оценка коэффициента регрессии в модели парной регрессии  по
по  ) случайный остаток
) случайный остаток  будет интегрируемым временным рядом порядка
будет интегрируемым временным рядом порядка  . Если же
. Если же  , то константа
, то константа  может быть подобрана так, что
может быть подобрана так, что  будет стационарным (или интегрируемым порядка 0) с нулевым средним. При этом вектор (1; -
будет стационарным (или интегрируемым порядка 0) с нулевым средним. При этом вектор (1; - ) (или любой другой, отличающийся от этого сомножителем) называется коинтегрирующим. При регрессионном анализе временных рядов
) (или любой другой, отличающийся от этого сомножителем) называется коинтегрирующим. При регрессионном анализе временных рядов  и
и  их коинтеграция (согласование порядков их интегрируемости) производится обычно по следующей схеме:
их коинтеграция (согласование порядков их интегрируемости) производится обычно по следующей схеме:
1) рассматривается модель  и строится МНК-оценка
и строится МНК-оценка  для параметра
для параметра  ;
;
2) ряд  анализируется на стационарность в рамках одной из моделей APCC(p,q); например, в рамках АР(1)-модели проверяется гипотеза |
анализируется на стационарность в рамках одной из моделей APCC(p,q); например, в рамках АР(1)-модели проверяется гипотеза | | < 1 в представлении
| < 1 в представлении  ;
;
3) если результат отрицательный, то возвращаются к спецификации исходной модели, пробуя в качестве зависимой и объясняющей переменных различные варианты  и
и  .
.
3) Системы одновременных уравнений (СОУ). Выше был приведён пример системы одновременных линейных уравнений (см. (3.1)-(3.3)), дано определение СОУ (см. (3.4)) и рассмотрены основные проблемы, возникающие при их построении и анализе (спецификация, идентифицируемость, идентификация и верификация). Неприменимость (в общем случае) обычного МНК как средства получения состоятельных оценок для неизвестных параметров СОУ инициировала разработку ряда специальных методов идентификации СОУ: косвенного МНК, двух- и трёхшагового методов наименьших квадратов (2МНК и ЗМНК), метода максимального правдоподобия с ограниченной и с полной информацией, метода инструментальных переменных и др. Поэтому правомерно выделить проблематику построения и анализа СОУ в качестве одного из трёх основных разделов эконометрики.
В общих чертах образ действий при идентификации СОУ может быть описан следующим образом (далее используются обозначения, принятые в соотношениях (3.4) и (3.5)).
а) методы статистического оценивания параметров СОУ подразделяются на два класса:
1) методы, предназначенные для оценки параметров одного отдельно взятого уравнения системы (МНК, косвенный МНК, 2МНК, метод максимального правдоподобия с ограниченной информацией);
2) методы, предназначенные для одновременного оценивания параметров всех уравнений системы с учётом их взаимосвязей (ЗМНК, метод максимального правдоподобия с полной информацией).
б) Если уравнения структурной формы модели могут быть расположены в таком порядке, что уравнение  (i = l,2,...,m) может содержать в качестве объясняющих эндогенных переменных только переменные
(i = l,2,...,m) может содержать в качестве объясняющих эндогенных переменных только переменные  (или часть из них), а случайное возмущение
(или часть из них), а случайное возмущение  этого уравнения не коррелирует со всеми этими эндогенными переменными, то такая система называется рекурсивной, и последовательное применение к каждому уравнению такой системы обычного МНК даёт состоятельные оценки её структурных параметров. Класс рекурсивных систем является простейшим с точки зрения решения задачи оценивания структурных параметров СОУ.
этого уравнения не коррелирует со всеми этими эндогенными переменными, то такая система называется рекурсивной, и последовательное применение к каждому уравнению такой системы обычного МНК даёт состоятельные оценки её структурных параметров. Класс рекурсивных систем является простейшим с точки зрения решения задачи оценивания структурных параметров СОУ.
в) Если исследователя интересуют только параметры приведённой формы и задача прогноза эндогенных переменных, то он может ограничиться применением обычного метода наименьших квадратов к каждому отдельному уравнению приведённой формы (с последующей оценкой, если это необходимо, идентифицируемых параметров структурной формы). Такой образ действий называют косвенным методом наименьших квадратов, или методом наименьших квадратов без ограничений, а оценки, полученные с его помощью, будут состоятельными.
г) В ситуациях, когда среди уравнений системы имеются не-идентифицируемые, так же как и в случаях, когда оценивание и анализ параметров структурной формы представляют для исследователя самостоятельный интерес, обычно применяют двухшаговый метод наименьших квадратов (2МНК). Этот метод предназначен для оценивания параметров отдельного уравнения структурной формы, а его последовательное применение к каждому из уравнений структурной формы СОУ позволяет получить состоятельные оценки всех структурных параметров (хотя 2МНК и не учитывает возможные взаимосвязи между уравнениями системы).
д) Сущность двух шагов 2МНК заключается в следующем. На 1-м шаге для каждой эндогенной переменной, играющей роль объясняющей в анализируемом уравнении структурной формы, с помощью обычного МНК строится регрессия на все предопределённые переменные  . На 2-м шаге эта эндогенная переменная заменяется в рассматриваемом уравнении её регрессионным выражением через
. На 2-м шаге эта эндогенная переменная заменяется в рассматриваемом уравнении её регрессионным выражением через  , после чего в правой части этого уравнения остаются только предопределённые переменные и к нему применяется обычный МНК. В моделях с большим числом предопределённых переменных в целях снижения размерности рекомендуется на 1-м шаге строить регрессию предикторной эндогенной переменной не на все предопределённые переменные, а лишь на небольшое число их главных компонент.
, после чего в правой части этого уравнения остаются только предопределённые переменные и к нему применяется обычный МНК. В моделях с большим числом предопределённых переменных в целях снижения размерности рекомендуется на 1-м шаге строить регрессию предикторной эндогенной переменной не на все предопределённые переменные, а лишь на небольшое число их главных компонент.
е) Если структурные случайные возмущения  различных уравнений системы взаимно коррелированы, то для оценивания структурных параметров рекомендуется применять другие методы, например, трёхшаговый метод наименьших квадратов (3МНК). Этот метод предназначен для одновременного оценивания структурных параметров всех уравнений системы и даёт их состоятельные оценки, по эффективности превосходящие оценки (тоже состоятельные) 2МНК.
различных уравнений системы взаимно коррелированы, то для оценивания структурных параметров рекомендуется применять другие методы, например, трёхшаговый метод наименьших квадратов (3МНК). Этот метод предназначен для одновременного оценивания структурных параметров всех уравнений системы и даёт их состоятельные оценки, по эффективности превосходящие оценки (тоже состоятельные) 2МНК.
ж) ЗМНК использует полученные на первых двух шагах 2МНК оценки структурных параметров для вычисления оценки ковариационной матрицы возмущений различных уравнений структурной формы. Затем на 3-м шаге оценки структурных параметров системы пересчитываются с помощью обобщённого МНК в рамках соответствующей схемы обобщённой линейной модели множественной регрессии, в которой в качестве ковариационной матрицы остатков используется полученная ранее оценка ковариационной матрицы возмущений.
з) В ряде ситуаций могут оказаться полезными и другие методы статистического оценивания параметров СОУ. Для оценивания параметров одного отдельно взятого уравнения — это, например, метод максимального правдоподобия с ограниченной информацией (требующий, правда, дополнительного априорного предположения о нормальном характере распределения структурных возмущений модели), для одновременной оценки всех структурных параметров системы может использоваться метод максимального правдоподобия с полной информацией.
и) Одна из главных конечных прикладных целей построения и анализа эконометрических моделей в виде СОУ — это точечный и интервальный прогноз эндогенных переменных по заданным значениям предопределённых переменных и связанная с этим задача проведения многовариантных сценарных расчётов, показывающих, как будут «себя вести» эндогенные переменные при различных сочетаниях значений предопределённых переменных. «Точечное» решение этих задач основано на подсчёте значений эндогенных переменных с помощью статистически оценённой приведённой формы СОУ. Для получения «интервальных» вариантов решения необходимо уметь оценивать ковариационную матрицу ошибок точечного прогноза, что является задачей аналитически достаточно сложной.
Структуризация перечисленных разделов эконометрики была основана на специфике типовых постановок решаемых в рамках каждого и этих разделов прикладных задач. Однако, говоря о содержании эконометрики, следует упомянуть и о развиваемом в рамках этой дисциплины методологическом базисе, компоненты которого могут использоваться при решении задач всех перечисленных выше типов. К основным составляющим этого методологического базиса, прежде всего, следует отнести:
• метод максимального правдоподобия;
• обобщённый метод моментов;
• теория больших выборок, или асимптотические результаты теории вероятностей;
• методы анализа панельных данных, т. е. многомерных исходных данных, регистрируемых на совокупности одних и тех же объектов в течение ряда тактов времени;
• непараметрические и полупараметрические методы статистики;
• статистические методы классификации: дискриминантный и кластер анализы;
• статистические методы снижения размерности: главные компоненты, факторный анализ и др.;
• теория имитационно-компьютерного эксперимента: метод Монте-Карло, бутстреп, перекрёстный компьютерный анализ дееспособности модели (cross-validation method) и др.
Правда, поскольку все эти направления исследований разрабатываются также и в рамках дисциплины «Математическая статистика», подчас трудно определить, какие из работ и научных результатов данной проблематики следует отнести к эконометрике, а какие - к математической статистике. Отличительной особенностью эконометрических работ является такая модификация классических постановок задач, которая инициируется спецификой именно экономических приложений.
Литература
1.Андерсон Т.Статистический анализ временных рядов, пер. с англ., М., !976
2. Липцер Р. Ш., Ширяев А. Н., Статистика случайных процессов, М., 1974
3. Бриллинджер Д., Временные ряды, Обработка данных и теория., пер. с англ., М., 1980
4. Кендалл М., Стюарт А., Статистические выводы и связи, пер. с англ., М., 1973
5. Крамер Г., Математические методы статистики, пер. с англ, 2 изд., М., 1975
6. Ципкин Я. 3., Адаптация и обучение в автоматических системах, М., 1968.
7. Вазан М. Стохастическая аппроксимация, М., 1972;
8.Невельсон М. Б., Хасьмииский Р. 3., Стохастическая аппроксимация и рекуррентное оценивание, М., 1972.
9. Ермольев Ю. М., Методы стохастического программирования, М., 1976.
10. Закс Ш., Теория статистических выводов, пер. с англ., М., 1975.
11. Ермаков С. М., Михайлов Г. А., Статистическое моделирование, 2 изд., М., 1982.
12. Дуб Дж. Л., Вероятностные процессы, М., 1956.
13. Розанов Ю. А., Стационарные случайные процессы, М., 1963.
14.Чжун К. Л., Однородные цепи Маркова, М., 1964.
15. Ибрагимов И. А., Розанов Ю. А., Гауссовскнс случайные процессы, М., 1970.
16.Севастьянов Б. А., Ветвящиеся процессы, М., 1971.
17. Гихман И. И., Скороход А. В., Теория случайных процессов, т. 1—3, М., 1971, 1973, 1975.
18. Гихман И. И., Скороход А. В., Введение в теорию случайных процессов, М., 1977.
19. Вентцель А. Д., Курс теории случайных процессов, М., 1976.
20.Ширяев А. Н., Вероятность, М., 1980.
21. Боровков А. А., Теория вероятностей, М., 1986.
22. Дуб Дж.Л., Вероятностные процессы, М., 1956.
23. Чжуи К. Л., Одпородные цепи Маркова, М., 1964.
24 Вентцель А. Д., Курс теории случайных процессов, М., 1976.
25. Л и Ц., Джадж Д., Зель-нер А., Оценивание параметров марковских моделей по агрегированным временным рядам, М., 1977.
26. Ширяев А. Н., Вероятность, М., 1980.
27. Billingslcy P., Statistical Methods in Markov chains, Ann. Math. Stat., v. 32, № 1, 1961.
28. Дуб Дж.Л., Вероятностные процессы, М., 1956
29. Розанов Ю. А., Стационарные случайные процессы, М., 1963
30. Чжуи К Л., Однородные цепи Маркова, М., 1964.
31 Ибрагимов И. А., Розанов Ю. А., Гауссовские случайные процессы, М., 1970.
32 Гихман И. И., Скороход А. В., Теория случайных процессов, т. 1 —3, М., 1971, 1973, 1975.
33 Гихман И. И., Скороход А. В., Введение в теорию случайных процессов, М., 1977.
34. Севастьянов Б. А., Ветвящиеся процессы, М., 1971.
35. Вентцель А. Д., Курс теории случайных процессов, М., 1976.
36 Ширяев А. Н., Вероятность, М., 1980.
37. Вальд А., Статистические решающие функции, в сб.: Позиционные игры, М., 1967.
38 Вальд А., Последовательный анализ, М., 1960.
39. Леман Э., Проверка статистических гипотез, М., 1979.
40. Ивченко Г. И., Медведев А. И., Математическая статистика, М., 1984.
41. Berger J. О, Statistical Decision theory, N. Y. - Berlin, 1984.
42. .: Липцср Р. Ш., Ширяев А. Н., Статистика случайных процессов, М., 1974
43. Ибрагимов И.А., Хасьминский Р.З., Асимптотическая теория оценивания, М., 1974
44. Айвазян С. А., Енюков И. С, Мешалкин Л. Д., Прикладная статистика. Основы моделирования и первичная обработка данных, М., 1983
45. Айвазян С. А., Енюков И. С, Мешалкин Л. Д., Прикладная статистика. Исследование зависимостей, М., 1983
46. Хьюбер П., Робастпость в статистике, М., 1984
47. Рао С. Р., Линейные статистические методы и их применения, пер. с англ., М., 1968.
48. Кендалл М.Дж., Стьюарт А., Статистические выводы и связи, пер. с англ., М., 1973
49. Тюрин Ю.Н., ВНИИ системных исследований, сб. трудов, вып. 11, М, 1984
50. Линник Ю. В., Метод наименьших квадратов и основы ма-тематико-статнстичсской теории обработки наблюдений, 2 изд., М., 1962
51. Рао С. Р., Линейные статистические методы и их применения, М., 1968
52. Альберт А., Регрессия, псевдоинверсия и рекуррентное оценивание, М., 1977
53. Себер Дж., Линейный регрессионный анализ М., 1980
54. Вересков А. И., Федоров В. В., Методы решения нестандартных регрессионных задач, в сб.: «Статистические модели и методы», М., 1984
55. Дрейпер Н., Смит Г., Прикладной регрессионный анализ, 2 изд., М., 1986
56. Айвазян С.А.. Бежаева 3. И., Староверов В., Классификация многомерных наблюдений, М., 1974
57. Fisher R. A., Ann. of Eugenics, 1936, v. 7, p.179-88.
58. Шеффе Г., Дисперсионный анализ, пер. с англ., М., 1963
59. Кендалл М.Дж.,Стьюарт А., Многомерный статистический анализ и временные ряды, пер. с англ., М., 1976
60. Болч Б., Хуапь К.Дж., Многомерные статистические методы для экономики, пер. с англ., М., 1979
61. Себер Дж., Линейный регрессионный анализ, пер. с англ., М., 1980
62. Айвазян С.А., Енюков И.С., Мешалкин Л.Д., Прикладная статистика: исследование зависимостей, М., 1985
63. Айвазян С.А., Основы эконометрики, 2-е изд., М., 2001
64. Магнус Я.Р., Катышев П.К., Пересецкий А.А., Эконометрика. Начальный курс, 3-е изд., М., 2000
65. Харман Г., Современный факторный анализ, М., 1972
66. Айвазян С.А., Бежаева 3. И., Староверов О.В., Классификация многомерных наблюдений, М., 1974
67. Иберла К., Факторный анализ, М., 1980
68. Благуш П., Факторный анализ с обобщениями, М., 1989
69 Андерсон Т., Введение в многомерный статистический анализ, пер. с англ., М., 1963
70. Кендалл М. Дж., Стьюарт Ф., Многомерный статистический анализ и временные ряды, пер. с англ., М. 1976
71. Большев Л. Н., «Bull. Int. Stat. Inst.», 1969, №43, p. 425-41
72. Wishart J., «Biometrika», 1928, v. 20A, p. 32-52
73. Hotelling H. «Ann. Vath. Stat.», 1931, v. 2, p. 360-78
74. Kruskal J. В., «Psychomet rika», 1964, v. 29, p. 1-27
75. Айвазян С. А., Бухштабср В.М. Енюков И.С, Мешалкин Л. Д., Прикладная статистика: классификация и снижение размерности, М., 1989
76. Айвазян С. А. Енюков И. С, Мешалкин Л. Д., Прикладная статистика: исследование зависимостей, М., 1985
77. Соболь И.М., Численные методы Монте-Карло, М., 1973
78. Ермаков СМ., Михайлов Г.А., Статистическое моделирование, М., 1982
79. Форрестер Дж., Основы кибернетики предприятия, М., 1971
80. Нэйлор Т., Машинные имитационные эксперименты с моделями экономических систем, М., 1975
81. Яковлев Е.И., Машинная имитация, М., 1975
82. Геронимус Ю.В., Имитационное моделирование и системность, «Экономика и математические методы», 1985, т. XXI
83.Модельные эксперименты с механизмами экономического управления, М., 1989.
метод главных компонент, анализ канонических корреляций
статистика Хотеллинга
анализ канонических корреляций
смеси вероятностных распределений, многомерное шкалирование
конфлюентного анализа
методам экстремальной группировки признаков
Бесплатная лекция: "Логика изложения" также доступна.
методы решения простой и обобщённой задачи о собственных значениях и векторах; простое обращение и псевдообращение матриц; процедуры диагонализации матриц
корреляционная функция и спектральная функция
периодограмма
Интеграл Лебега
В рамках этого понятия рассматриваются бейесовские и минимаксные статистические оценки.
[1] Айвазян С. А., Основы эконометрики, М., 2001





















