Фактор времени в экономических измерениях
27. Фактор времени в экономических измерениях
Оглавление
В экономической деятельности хозяйствующих субьектов постоянно возникают проблемы соизмерения ценности денежных средств, выплачиваемых или получаемых в разные моменты времени. Так, коммерческие организации, располагая свободными денежными средствами, имеют альтернативные возможности их использования - инвестирование производства с целью расширения обьемов производства и получения дополнительной прибыли, вложение денежных средств на депозитный счет в банк, покупка ценных бумаг и др. Аналогичными возможностями обладают и домашние хозяйства.
Обладая альтернативными возможностями инвестированиия денежных средств, потенциальный инвестор стремится максимизировать свою экономическую выгоду ( доход, прибыль). Можно сформулировать следующее общее правило выбора - если в любое время кумулятивный денежный поток по одной из альтернатив А, по крайней мере, не меньше кумулятивного денежного потока другой альтернативы В, и имеется хотя бы один момент времени, когда поток А превышает поток В, то альтернатива А экономически предпочтительнее В.
Поэтому при рассмотрении двух альтернатив вложений при условии равной степени риска инвестирования (рис. 2.3,а), инвестор, очевидно, предпочтет альтернативу А.
Однако во многих случаях ситуация ялвяется более сложной. В частности, как это видно на рис. 2.3, б, при сравнении альтернатив А и С достаточно сложно принять решение о предпочтительности одной из рассматриваемых альтернатив. Для решения этой проблемы требуется установление некоего масштаба (шкалы измерения), посредством которого можно соизмерить ценность денежных потоков во времени.
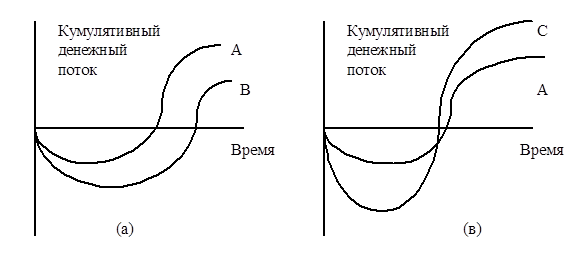
2.3. Кумулятивные денежные потоки альтернативных проектов
Необходимость такого соизмерения состоит в том, что ценность любой денежной единицы в текущий момент времени всегда выше, чем ее ценность в будущем. Одной из причин этого является инфляция как процесс падения покупательной срособности денег во времени. Однако, если отвлечься от современных российских реалий, для которых характерен достаточно высокий уровень инфляции, и представить гипотетическую ситуацию ее отсутствия, то и здесь деньги ценятся во времени по-разному, поскольку они обладают “зарабатывающей силой”. Доказательством этого могут служить результаты финансовых инвестиций в форме процентных доходов, получаемых вкладчиком по депозитным счетам в коммерческих банках. Приведенный ниже пример иллюстрирует “зарабатывающую силу” денег в результате материальных инвестиций.
Рекомендуемые материалы
ПРИМЕР.
Допустим, рабочий ручным способом копает канавы для подземного кабеля. За эту работу ему платят 8 руб. за метр, а в среднем он копает 10 метров в день. Погодные условия ограничивают продолжительность работы до 180 дней в году. Таким образом, он зарабатывает 80 руб за день работы или 14400 руб в год. Он может купить электрический канавокопатель за 8000 руб.
Рабочий может купить механический канавокопатель, взяв взаймы 8000 руб под 30% годовых. Машина будет копать в среднем 40 метров в день. Снизив цену до 5 руб. за метр, рабочий может получить достаточно заказов, чтобы загрузить машину, когда будут позволять погодные условия.
Расчетные эксплуатационные затраты на обслуживание канавокопательной машины составляют 40 руб за рабочий день. Через год машина полностью обесценивается вследствие физического износа.
Таблица 2.2
| Поступления | 44000 |
| Заем | 8000 |
| Выручка от реализации (оплата за работу) ,180 дней´40 метр´5 | 36000 |
| Платежи | 25600 |
| Покупка машины | 8000 |
| Эксплуатационные затраты на обслуживание, 180 дней ´ 40 | 7200 |
| Проценты за кредит, 8,000 ´ 0,3 | 2400 |
| Возврат кредита | 8000 |
| Поступления минус платежи | 18400 |
| Чистый доход от покупки машины (18400 - 14400) | 4000 |
Как видно из приведенного примера, привлечение заемных средств при выгодном их вложении позволяет увеличить доходы, которых достаточно для возврата займа и получения дополнительной прибыли. Другими словами, деньги, не только помещенные на депозит, но и вложенные в инвестиционный проект, обладают “зарабатывающей силой”.
Следовательно, результат любой экономической деятельности, выраженный в стоимостной форме, т.е. в форме дохода, представляется как некая сумма “сегодняшнего дня”, эквивалентная будущим доходам. В соответствии с этим, будущие доходы могут быть приведены на эквивалентную основу путем умножения на дисконтирующий множитель q, меньший единицы и показывающий во сколько раз ценность денежной единицы, получаемой в будущем, меньше ценности этой денежной единицы в текущий момент. При этом множитель q, как правило, определяется выражением
q ,
,
где R - ставка дисконтирования.
С помощью процедуры, обратной дисконтированию, можно определить будущую сумму, эквивалентную сегодняшней сумме. При этом сегодняшняя сумма умножается на коэффициент 1/q = (1+R).
Такой подход вполне правомерен и из него вытекает банковская форма денежного кредита как средства извлечения постоянного дохода путем предоставления займов (ссуд) действующим предпринимателям, которые трансформируют заемные средства в реальный капитал, наращиваемый в ходе воспроизводственного процесса.
Поскольку в основе дисконтирования лежат расчетные процедуры, связанные с процентной ставкой, используемой на рынке капитала, целесообразно кратко охарактеризовать их сущность.
Под процентами (процентными деньгами) понимается сумма доходов от предоставления финансовых средств в долг в любой форме. При заключении финансового соглашения о предоставлении кредита стороны договариваются о размере процентной ставки, определяемой как соотношение суммы процентных денег, выплачиваемых за фиксированный отрезок времени, к величине кредита. Обычно в качестве фиксированного отрезка принимается год.
При установлении процентной ставки кредитор учитывает следующие основные факторы:
· риск невозврата должником кредитуемой суммы;
· затраты кредитора на изучение должника и оформление кредита;
· упущенные возможности альтернативного использования кредитором кредитуемой суммы.
К факторам, определяющим величину процентной ставки с точки зрений должника, следует отнести условие, что ожидаемая доходность заемных средств должна превышать затраты на оплату процентов.
Существуют два способа начисления процентов - простые и сложные проценты. Отличие в способах состоит в выборе исходной базы для начисления процентов, а также в порядке возврата кредитуемых средств.
Простой процент - это способ начисления процентов только на начальную инвестируемую сумму денежных средств. При таком способе начальная сумма денежных средств PV за определенный промежуток времени, в течение которого n раз начисляются проценты, возрастет до величины FV:
FV = PV * (1+R* n)
где R - процентная ставка, установленная на определенный промежуток времени.
ПРИМЕР.
Допустим, что берется в долг 1000 руб. по ставке простого процента 30% годовых. В конце первого года процент, подлежащий к оплате, составляет
I= 1000(1)(0.3) =300
С учетом самого долга и процентов сумма FV, подлежащая оплате на конец года, составит 1300 руб.
Сложный процент - это способ начисления процентов, при котором начальная инвестируемая сумма PV через промежуток времени, в течение которого n раз начисляются проценты, возрастет до величины FV:
FV = PV * (1+R) n.
В отличие от первого способа здесь начисление процентов производится на сумму, включающую проценты, начисленные за предыдущие периоды. Такой метод исходит из предположения, что все выплаты по процентам (процентные деньги) реинвестируются и приносят такой же процент дохода.
ПРИМЕР.
Допустим, что берется в долг 1000 руб. по ставке простого процента 30% годовых на два года. Долг вместе с процентами выплачивается в конце срока кредитования. В конце первого года процент, подлежащий оплате, составляет
I = 1000(1)(0.3) = 300,
а в конце второго года
I = 300 + (1000+300)*(0.3) =(1000)*[(1+0.3) 2 - 1]=[PV1] 690.
Следует отметить, что метод простых процентов является частным случаем метода сложных процентов, при котором проценты погашаются регулярно в момент их начисления. Как видно из расчетов, приведенных в табл. 2.3, при ежегодной выплате процентов действует формула простых процентов.
Таблица 2.3
Вычисление сложного процента, когда проценты выплачиваются ежегодно
| Годы | Сумма долга на начало года (А) | Процент к оплате на конец года (В) | Сумма долга на конец года (А+В) | Сумма, опплаченная в конце года |
| 1 | 1000 | 300 | 1300 | 300 |
| 2 | 1000 | 300 | 1300 | 300 |
| 3 | 1000 | 300 | 1300 | 300 |
| 4 | 1000 | 300 | 1300 | 1300 |
Если же проценты накапливаются (табл. 2.4), то начисление производится по методу сложных процентов.
Таблица 2.4
Вычисление сложного процента, когда проценты накапливаются
| Годы | Сумма долга на начало года (А) | Процент к оплате на конец года (В) | Сумма долга на конец года (А+В) | Сумма, опплаченная в конце года |
| 1 | 1000 | 1000´0.3= 300 | 1000x1.3=1300 | 0 |
| 2 | 1300 | 1300´0.3= 390 | 1000(1.3)2=1690 | 0 |
| 3 | 1690 | 1690 ´ 0.3= 507 | 1000(1.3)3=2197 | 0 |
| 4 | Обратите внимание на лекцию "9 Холодные супы". 2197 | 2197 ´ 0.3 =659 | 1000(1.3)4=2856 | 2856 |
Рассмотренные методы могут быть распространены на сферу оценки любых финансовых операций, а метод сложных процентов может использоваться для соизмерения ценности денежных потоков во времени. Действительно, если собственник капитала располагает суммой денежных средств PV, то вложив их в некоторый источник накопления капитала, гарантирующий ему определенный доход по ставке R процентов в год, собственник через период времени Т получает доход:
FV = PV * (1+R) n
Отсюда следует, что сумма PV является для собственника денежным эквивалентом суммы FV через n лет, а величина PV, определяемая выражением:
![]() ,
,
является текущим эквивалентом суммы FV, полученной через n лет.
[PV1]Àìîðòèçàöèîííûå îò÷èñëåíèÿ ÿâëÿþòñÿ ïî ôîðìå íîìèíàëüíûìè äåíåæíûìè çàòðàòàìè. Îíè âêëþ÷àþòñÿ â ñîñòàâ çàòðàò ýêîíîìè÷åñêîãî ñóáúåêòà, óìåíüøàÿ íàëîãîîáëàãàåìóþ ïðèáûëü. Îäíàêî, ðåàëüíî àìîðòèçàöèîííûå îò÷èñëåíèÿ íå âûïëà÷èâàþòñÿ âíåøíèì àãåíòàì è àêêóìóëèðóþòñÿ ýêîíîìè÷åñêèì ñóáúåêòîì.



 ,
,

















