Асимметричные криптосистемы
4. Асимметричные криптосистемы
4.1. Концепция криптосистемы с открытым ключом
Эффективными системами криптографической защиты данных являются асимметричные криптосистемы, называемые также криптосистемами с открытым ключом. В таких системах для зашифрования данных используется один ключ, а для расшифрования – другой ключ (отсюда и название – асимметричные). Первый ключ является открытым и может быть опубликован для использования всеми пользователями системы, которые зашифровывают данные. Расшифрование данных с помощью открытого ключа невозможно.
Для расшифрования данных получатель зашифрованной информации использует второй ключ, который является секретным. Разумеется, ключ расшифрования не может быть определен из ключа зашифрования.
Обобщенная схема асимметричной криптосистемы с открытым ключом показана на рис. 4.1. В этой криптосистеме применяют два различных ключа: Кв – открытый ключ отправителя А; kв – секретный ключ получателя В. Генератор ключей целесообразно располагать на стороне получателя В (чтобы не пересылать секретный ключ kв по незащищенному каналу). Значения ключей Кв и kв зависят от начального состояния генератора ключей.
Раскрытие секретного ключа kв по известному открытому ключу Кв должно быть вычислительно неразрешимой задачей.
Характерные особенности асимметричных криптосистем:
1. Открытый ключ Кв и криптограмма С могут быть отправлены по незащищенным каналам, т.е. противнику известны Кв и С.
2. Алгоритмы шифрования и расшифрования
Рекомендуемые материалы
Ев : М ® С,
Dв : С ® М
являются открытыми.
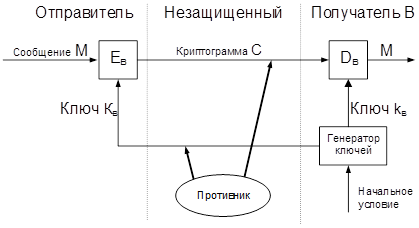
Рисунок 4.1 – Обобщенная схема асимметричной криптосистемы с открытым ключом
Защита информации в асимметричной криптосистеме основана на секретности ключа kв.
У.диффи и м.хеллман сформулировали требования, выполнение которых обеспечивает безопасность асимметричной криптосистемы:
1. Вычисление пары ключей (Кв, kв) получателем В на основе начального условия должно быть простым.
2. Отправитель А, зная открытый ключ Кв и сообщение М, может легко вычислить криптограмму
С =  (М) = Ев (М). (4.1)
(М) = Ев (М). (4.1)
3. Получатель В, используя секретный ключ kв и криптограмму С, может легко восстановить исходное сообщение
М =  (С) = Dв(С) = Dв [Ев(М)]. (4.2)
(С) = Dв(С) = Dв [Ев(М)]. (4.2)
4. Противник, зная открытый ключ Кв, при попытке вычислить секретный ключ kв наталкивается на непреодолимую вычислительную проблему.
5. Противник, зная пару (Кв, С), при попытке вычислить исходное сообщение М наталкивается на непреодолимую вычислительную проблему [28].
4.2. Однонаправленные функции
Концепция асимметричных криптографических систем с открытым ключом основана на применении однонаправленных функций. Неформально однонаправленную функцию можно определить следующим образом. Пусть X и Y – некоторые произвольные множества. Функция
f : X ® Y
является однонаправленной, если для всех xÎX можно легко вычислить функцию
y = f (x), где yÎY.
И в то же время для большинства yÎY достаточно сложно получить значение xÎX, такое, что f (x)=y (при этом полагают, что существует по крайней мере одно такое значение x).
Основным критерием отнесения функции f к классу однонаправленных функций является отсутствие эффективных алгоритмов обратного преобразования Y ® X.
В качестве первого примера однонаправленной функции рассмотрим целочисленное умножение. Прямая задача – вычисление произведения двух очень больших целых чисел P и Q, т.е. нахождение значения
N = P*Q, (4.3)
является относительно несложной задачей для ЭВМ.
Обратная задача – разложение на множители большого целого числа, т.е. нахождение делителей P и Q большого целого числа N = P*Q, является практически неразрешимой задачей при достаточно больших значениях N. По современным оценкам теории чисел при целом N»2664 и P»Q для разложения числа N потребуется около 1023 операций, т.е. задача практически неразрешима на современных ЭВМ.
Следующий характерный пример однонаправленной функции – это модульная экспонента с фиксированными основанием и модулем. Пусть A и N – целые числа, такие, что 1£ А < N. Определим множество ZN:
ZN = {0, 1, 2, ..., N –1}.
Тогда модульная экспонента с основанием А по модулю N представляет собой функцию
fA,N : ZN ® ZN,
fA,N (x) = Ax (mod N), (4.4)
где X – целое число, 1£ x £ N –1.
Существуют эффективные алгоритмы, позволяющие достаточно быстро вычислить значения функции fA,N (x).
Если y = Ax, то естественно записать x = logA (у).
Поэтому задачу обращения функции fA,N(x) называют задачей нахождения дискретного логарифма или задачей дискретного логарифмирования.
Задача дискретного логарифмирования формулируется следующим образом. Для известных целых A, N, Y найти целое число X, такое, что
Ax mod N = y.
Алгоритм вычисления дискретного логарифма за приемлемое время пока не найден. Поэтому модульная экспонента считается однонаправленной функцией.
По современным оценкам теории чисел при целых числах A » 2664 и N » 2664 решение задачи дискретного логарифмирования (нахождение показателя степени x для известного y) потребует около 1026 операций, т.е. эта задача имеет в 103 раз большую вычислительную сложность, чем задача разложения на множители. При увеличении длины чисел разница в оценках сложности задач возрастает.
Следует отметить, что пока не удалось доказать, что не существует эффективного алгоритма вычисления дискретного логарифма за приемлемое время. Исходя из этого, модульная экспонента отнесена к однонаправленным функциям условно, что, однако, не мешает с успехом применять ее на практике.
Вторым важным классом функций, используемых при построении криптосистем с открытым ключом, являются так называемые однонаправленные функции с "потайным ходом" (с лазейкой). Дадим неформальное определение такой функции. Функция
f : X ® Y
относится к классу однонаправленных функций с "потайным ходом" в том случае, если она является однонаправленной и, кроме того, возможно эффективное вычисление обратной функции, если известен "потайной ход" (секретное число, строка или другая информация, ассоциирующаяся с данной функцией).
В качестве примера однонаправленной функции с "потайным ходом" можно указать используемую в криптосистеме RSA модульную экспоненту с фиксированными модулем и показателем степени. Переменное основание модульной экспоненты используется для указания числового значения сообщения M либо криптограммы C
4.3. Криптосистема шифрования данных RSA
Алгоритм RSA предложили в 1978 г. три автора: Р.Райвест (Rivest), А.Шамир (Shamir) и А.Адлеман (Adleman). Алгоритм получил свое название по первым буквам фамилий его авторов. Алгоритм RSA стал первым полноценным алгоритмом с открытым ключом, который может работать как в режиме шифрования данных, так и в режиме электронной цифровой подписи.
Надежность алгоритма основывается на трудности факторизации больших чисел и трудности вычисления дискретных логарифмов.
В криптосистеме RSA открытый ключ Кв, секретный ключ kв, сообщение М и криптограмма С принадлежат множеству це-лых чисел
ZN = {0, 1, 2, ..., N –1}, (4.5)
где N – модуль:
N = P*Q. (4.6)
Здесь P и Q – случайные большие простые числа. Для обеспечения максимальной безопасности выбирают P и Q равной длины и хранят в секрете.
Множество ZN с операциями сложения и умножения по модулю N образует арифметику по модулю N.
Открытый ключ Кв выбирают случайным образом так, чтобы выполнялись условия:
1< Кв £ j (N), НОД (Кв, j (N)) =1, (4.7)
j (N)=(P –1) (Q –1), (4.8)
где j (N) – функция Эйлера.
Функция Эйлера j (N) указывает количество положительных целых чисел в интервале от 1 до N, которые взаимно проcты с N.
Второе из указанных выше условий означает, что открытый ключ Кв и функция Эйлера j (N) должны быть взаимно простыми.
Далее, используя расширенный алгоритм Евклида, вычисляют секретный ключ kв, такой, что
kв * Кв º 1 (mod j (N)) (4.9)
или
kв = Кв–1 (mod (P –1)(Q –1)).
Это можно осуществить, так как получатель В знает пару простых чисел (P,Q) и может легко найти j (N). Заметим, что kв и N должны быть взаимно простыми.
Открытый ключ Кв используют для шифрования данных, а секретный ключ kв – для расшифрования.
Преобразование шифрования определяет криптограмму С через пару (открытый ключ Кв, сообщение М) в соответствии со следующей формулой:
C =  (M) = EВ (M) =
(M) = EВ (M) =  (mod N). (4.10)
(mod N). (4.10)
В качестве алгоритма быстрого вычисления значения C используют ряд последовательных возведений в квадрат целого M и умножений на M с приведением по модулю N.
Обращение функции C =  (mod N), т.е. определение значения M по известным значениям C, Кв и N, практически не осуществимо при N » 2 512.
(mod N), т.е. определение значения M по известным значениям C, Кв и N, практически не осуществимо при N » 2 512.
Однако обратную задачу, т.е. задачу расшифрования криптограммы С, можно решить, используя пару (секретный ключ kв, криптограмма С) по следующей формуле:
М =  (С) = DВ (C) =
(С) = DВ (C) =  (mod N). (4.11)
(mod N). (4.11)
Процесс расшифрования можно записать так:
DВ(EВ (М)) = М. (4.12)
Подставляя в (4.12) значения (4.10) и (4.11), получаем:
 = М (mod N)
= М (mod N)
или
 = M (mod N). (4.13)
= M (mod N). (4.13)
Величина j (N) играет важную роль в теореме Эйлера, которая утверждает, что если НОД (x, N) =1, то
xj(N) º 1 (mod N),
или в несколько более общей форме
xn×j(N)+1 º x (mod N). (4.14)
Сопоставляя выражения (4.13) и (4.14), получаем
Кв * kв = n * j (N) +1
или, что то же самое,
Кв * kв º1 (mod j (N)).
Именно поэтому для вычисления секретного ключа kв используют соотношение (4.9).
Таким образом, если криптограмму
C =  (mod N)
(mod N)
возвести в степень kв, то в результате восстанавливается исходный открытый текст М, так как
 =
=  = Mn×j(N)+1 º M (mod N).
= Mn×j(N)+1 º M (mod N).
Таким образом, получатель В, который создает криптосистему, защищает два параметра: 1) секретный ключ kв и 2) пару чисел (P,Q), произведение которых дает значение модуля N. С другой стороны, получатель В открывает значение модуля N и открытый ключ Кв.
Противнику известны лишь значения Кв и N. Если бы он смог разложить число N на множители P и Q, то он узнал бы "потайной ход" – тройку чисел {P,Q,Кв}, вычислил значение функции Эйлера
j (N) = (P –1) (Q –1)
и определил значение секретного ключа kв.
Однако, как уже отмечалось, разложение очень большого N на множители вычислительно не осуществимо (при условии, что длины выбранных P и Q составляют не менее 100 десятичных знаков).
4.3.1. Процедуры шифрования и расшифрования в
криптосистеме RSA
Предположим, что пользователь А хочет передать пользователю В сообщение в зашифрованном виде, используя криптосистему RSA. В таком случае пользователь А выступает в роли отправителя сообщения, а пользователь В – в роли получателя. Как отмечалось выше, криптосистему RSA должен сформировать получатель сообщения, т.е. пользователь В. Рассмотрим последовательность действий пользователя В и пользователя А.
1. Пользователь В выбирает два произвольных больших простых числа P и Q.
2. Пользователь В вычисляет значение модуля N = P * Q.
3. Пользователь В вычисляет функцию Эйлера
j (N) = (P –1) (Q –1)
и выбирает случайным образом значение открытого ключа Кв с учетом выполнения условий:
1< Кв £ j (N), НОД (Кв, j (N)) =1.
4. Пользователь В вычисляет значение секретного ключа kв, используя расширенный алгоритм Евклида при решении сравнения
kв º Кв–1 (mod j (N)).
5. Пользователь В пересылает пользователю А пару чисел (N, Кв) по незащищенному каналу.
Если пользователь а хочет передать пользователю в сообщение м, он выполняет следующие шаги.
6. Пользователь А разбивает исходный открытый текст М на блоки, каждый из которых может быть представлен в ви-де числа
Мi = 0, 1, 2, ..., N –1.
7. Пользователь А шифрует текст, представленный в виде последовательности чисел Мi по формуле
Ci =  (mod N)
(mod N)
и отправляет криптограмму
С1, С2, С3, ..., Ci, ...
пользователю B.
8. Пользователь В расшифровывает принятую криптограмму
С1, С2, С3, ..., Ci, ...,
используя секретный ключ kв, по формуле
Мi =  (mod N).
(mod N).
В результате будет получена последовательность чисел Мi, которые представляют собой исходное сообщение М. Чтобы алгоритм RSA имел практическую ценность, необходимо иметь возможность без существенных затрат генерировать большие простые числа, уметь оперативно вычислять значения ключей Кв и kв.
4.3.2. Безопасность и быстродействие криптосистемы
RSA
Безопасность алгоритма RSA базируется на трудности решения задачи факторизации больших чисел, являющихся произведениями двух больших простых чисел. Действительно, криптостойкость алгоритма RSA определяется тем, что после формирования секретного ключа kв и открытого ключа Кв "стираются" значения простых чисел Р и Q, и тогда исключительно трудно определить секретный ключ kв по открытому ключу Кв, поскольку для этого необходимо решить задачу нахождения делителей Р и Q модуля N.
Разложение величины N на простые множители Р и Q позволяет вычислить функцию j (N) = (P –1)(Q –1) и затем определить секретное значение kв, используя уравнение
Кв * kв º1 (mod j (N)).
Другим возможным способом криптоанализа алгоритма RSA является непосредственное вычисление или подбор значения функции
j (N) = (P –1)(Q –1). Если установлено значение j (n), то сомножители P и Q вычисляются достаточно просто. В самом деле, пусть
x = P + Q = N +1 – j (N),
y = (P – Q)2 = (Р + Q)2 – 4*N.
Зная j (N), можно определить x и затем y; зная x и y, можно определить числа Р и Q из следующих соотношений:
P = 1/2 (x + ), Q = 1/2 (x –
), Q = 1/2 (x – ).
).
Однако эта атака не проще задачи факторизации модуля N [28].
Задача факторизации является трудно разрешимой задачей для больших значений модуля N.
Сначала авторы алгоритма RSA предлагали для вычисления модуля N выбирать простые числа P и Q случайным образом, по 50 десятичных разрядов каждое. Считалось, что такие большие числа N очень трудно разложить на простые множители. Один из авторов алгоритма RSA, P. Pайвест, полагал, что разложение на простые множители числа из почти 130 десятичных цифр, приведенного в их публикации, потребует более 40 квадриллионов лет машинного времени. Однако этот прогноз не оправдался из-за сравнительно быстрого прогресса компьютеров и их вычислительной мощности, а также улучшения алгоритмов факторизации.
Ряд алгоритмов факторизации приведен в [45]. Один из наиболее быстрых алгоритмов, известных в настоящее время, алгоритм NFS (Number Field Sieve) может выполнить факторизацию большого числа N (с числом десятичных разрядов больше 120) за число шагов, оцениваемых величиной
 .
.
В 1994 г. было факторизовано число со 129 десятичными цифрами. Это удалось осуществить математикам А.Ленстра и М.Манасси посредством организации распределенных вычислений на 1600 компьютерах, объединенных сетью, в течение восьми месяцев. По мнению А.Ленстра и М.Манасси, их работа компрометирует криптосистемы RSA и создает большую угрозу их дальнейшим применениям. Теперь разработчикам криптоалгоритмов с открытым ключом на базе RSA приходится избегать применения чисел длиной менее 200 десятичных разрядов. Самые последние публикации предлагают применять для этого числа длиной не менее 250 – 300 десятичных разрядов.
Была сделана попытка расчета оценок безопасных длин ключей асимметричных криптосистем на ближайшие 20 лет исходя из прогноза развития компьютеров и их вычислительной мощности, а также возможного совершенствования алгоритмов факторизации. Эти оценки (табл.4.1.) даны для трех групп пользователей (индивидуальных пользователей, корпораций и государственных организаций), в соответствии с различием требований к их информационной безопасности. Конечно, данные оценки следует рассматривать как сугубо приблизительные, как возможную тенденцию изменений безопасных длин ключей асимметричных криптосистем со временем.
Таблица 4.1
Оценки длин ключей для асимметричных криптосистем, бит
| Год | Отдельные пользователи | Корпорации | Государственные организации |
| 1995 | 768 | 1280 | 1536 |
| 2000 | 1024 | 1280 | 1536 |
| 2005 | 1280 | 1536 | 2048 |
| 2010 | 1280 | 1536 | 2048 |
| 2015 | 1536 | 2048 | 2048 |
Криптосистемы RSA реализуются как аппаратным, так и программным путем.
Для аппаратной реализации операций зашифрования и расшифрования RSA разработаны специальные процессоры. Эти процессоры, реализованные на сверхбольших интегральных схемах (Сбис), позволяют выполнять операции RSA, связанные с возведением больших чисел в колоссально большую степень по модулю N, за относительно короткое время. И все же аппаратная реализация RSA примерно в 1000 раз медленнее аппаратной реализации симметричного криптоалгоритма DES.
Одна из самых быстрых аппаратных реализаций RSA с модулем 512 бит на сверхбольшой интегральной схеме имеет быстродействие 64 Кбит/с. Лучшими из серийно выпускаемых СБИС являются процессоры фирмы CYLINK, выполняющие 1024-битовое шифрование RSA.
Программная реализация RSA примерно в 100 раз медленнее программной реализации DES. С развитием технологии эти оценки могут несколько изменяться, но асимметричная криптосистема RSA никогда не достигнет быстродействия симметричных криптосистем.
Следует отметить, что малое быстродействие криптосистем RSA ограничивает область их применения, но не перечеркивает их ценность.
4.4. Схема шифрования Полига – Хеллмана
Схема шифрования Полига – Хеллмана [121] сходна со схемой шифрования RSA. Она представляет собой несимметричный алгоритм, поскольку используются различные ключи для шифрования и расшифрования. В то же время эту схему нельзя отнести к классу криптосистем с открытым ключом, так как ключи шифрования и расшифрования легко выводятся один из другого. Оба ключа (шифрования и расшифрования) нужно держать в секрете.
Аналогично схеме RSA криптограмма C и открытый текст P определяются из соотношений:
С = Ре mod n,
P = Cd mod n,
где e*d º1 (по модулю некоторого составного числа).
В отличие от алгоритма RSA в этой схеме число n не определяется через два больших простых числа; число n должно оставаться частью секретного ключа. Если кто-либо узнает значения e и n, он сможет вычислить значение d.
не зная значений e или d, противник будет вынужден вычислять значение
e = logP C (mod n).
Известно, что это является трудной задачей.
Схема шифрования Полига – Хеллмана запатентована в США и Канаде.
4.5. Схема шифрования Эль Гамаля
Схема Эль Гамаля, предложенная в 1985 г., может быть использована как для шифрования, так и для цифровых подписей. Безопасность схемы эль гамаля обусловлена сложностью вычисления дискретных логарифмов в конечном поле.
Для того чтобы генерировать пару ключей (открытый ключ – секретный ключ), сначала выбирают некоторое большое простое число Р и большое целое число G, причем G < P. Числа Р и G могут быть распространены среди группы пользователей.
Затем выбирают случайное целое число X, причем X<P. Число X является секретным ключом и должно храниться в секрете.
Далее вычисляют Y = GX mod P. Число Y является открытым ключом.
Для того чтобы зашифровать сообщение M, выбирают случайное целое число k, 1< k< p –1, такое, что числа к и (P –1) являются взаимно простыми.
Затем вычисляют числа
a = GK mod P,
b = YK M mod P.
Пара чисел (a,b) является шифртекстом. Заметим, что длина шифртекста вдвое больше длины исходного открытого текста М.
Для того чтобы расшифровать шифртекст (a,b), вычисляют
M = b/aX mod P. (*)
Поскольку
aX º GKX mod P,
b/aX ºYKM/aX º GKXM/GKX º M (mod P),
то соотношение (*) справедливо.
В реальных схемах шифрования необходимо использовать в качестве модуля P большое целое простое число, имеющее в двоичном представлении длину 512…1024 бит.
При программной реализации схемы Эль Гамаля [123] скорость ее работы (на SPARC-II) в режимах шифрования и расшифрования при 160-битовом показателе степени для различных длин модуля P определяется значениями, приведенными в табл.4.2.
Таблица 4.2
Скорости работы схемы Эль Гамаля
| Режим работы | Длина модуля, бит | ||
| 512 | 768 | 1024 | |
| Шифрование | 0,33 с | 0,80 с | 1,09 с |
| Расшифрование | 0,24 с | 0,58 с | 0,77 с |
4.6. Комбинированный метод шифрования
Главным достоинством криптосистем с открытым ключом является их потенциально высокая безопасность: нет необходимости ни передавать, ни сообщать кому бы то ни было значения секретных ключей, ни убеждаться в их подлинности. В симметричных криптосистемах существует опасность раскрытия секретного ключа во время передачи.
Oднако алгоритмы, лежащие в основе криптосистем с открытым ключом, имеют следующие недостатки:
· генерация новых секретных и открытых ключей основана на генерации новых больших простых чисел, а проверка простоты чисел занимает много процессорного времени;
· Процедуры шифрования и расшифрования, связанные с возведением в степень многозначного числа, достаточно громоздки.
Поэтому быстродействие криптосистем с открытым ключом обычно в сотни и более раз меньше быстродействия симметричных криптосистем с секретным ключом.
Комбинированный (гибридный) метод шифрования позволяет сочетать преимущества высокой секретности, предоставляемые асимметричными криптосистемами с открытым ключом, с преимуществами высокой скорости работы, присущими симметричным криптосистемам с секретным ключом. При таком подходе криптосистема с открытым ключом применяется для шифрования, передачи и последующего расшифрования только секретного ключа симметричной криптосистемы. А симметричная криптосистема применяется для шифрования и передачи исходного открытого текста. В результате криптосистема с открытым ключом не заменяет симметричную криптосистему с секретным ключом, а лишь дополняет ее, позволяя повысить в целом защищенность передаваемой информации. Такой подход иногда называют схемой электронного цифрового конверта.
Если пользователь а хочет передать зашифрованное комбинированным методом сообщение м пользователю в, то порядок его действий будет таков.
1. Создать (например, сгенерировать случайным образом) симметричный ключ, называемый в этом методе сеансовым ключом КS.
2. Зашифровать сообщение М на сеансовом ключе КS.
3. Зашифровать сеансовый ключ КS на открытом ключе КВ пользователя В.
4. Передать по открытому каналу связи в адрес пользователя В зашифрованное сообщение вместе с зашифрованным сеансовым ключом.
Действия пользователя в при получении зашифрованного сообщения и зашифрованного сеансового ключа должны быть обратными:
5. Расшифровать на своем секретном ключе kВ сеансовый ключ КS.
6. С помощью полученного сеансового ключа КS расшифровать и прочитать сообщение М.
При использовании комбинированного метода шифрования можно быть уверенным в том, что только пользователь В сможет правильно расшифровать ключ КS и прочитать сообщение М.
Таким образом, при комбинированном методе шифрования применяются криптографические ключи как симметричных, так и асимметричных криптосистем. Очевидно, выбор длин ключей для каждого типа криптосистемы следует осуществлять таким образом, чтобы злоумышленнику было одинаково трудно атаковать любой механизм защиты комбинированной криптосистемы.
В табл. 4.3. приведены распространенные длины ключей симметричных и асимметричных криптосистем, для которых трудность атаки полного перебора примерно равна трудности факто-ризации соответствующих модулей асимметричных криптосистем [121].
Таблица 4.3
Длины ключей для симметричных и асимметричных криптосистем при
одинаковой их криптостойкости
| Длина ключа симметричной криптосистемы, бит | Длина ключа асимметричной криптосистемы, бит |
| 56 | 384 |
| 64 | 512 |
| 80 | 768 |
| Рекомендуем посмотреть лекцию "18 Дизайн молекул лекарств". 112 | 1792 |
| 128 | 2304 |
Комбинированный метод допускает возможность выполнения процедуры аутентификации, т.е. проверки подлинности передаваемого сообщения. Для этого пользователь А на основе функции хэширования сообщения и своего секретного ключа kA с помощью известного алгоритма электронной цифровой подписи (ЭЦП) генерирует свою подпись и записывает ее, например, в конец передаваемого файла.
Пользователь В, прочитав принятое сообщение, может убедиться в подлинности цифровой подписи абонента А. Используя тот же алгоритм ЭЦП и результат хэширования принятого сообщения, пользователь В проверяет полученную подпись (см.гл.6). Комбинированный метод шифрования является наиболее рациональным, объединяя в себе высокое быстродействие симметричного шифрования и высокую криптостойкость, гарантируемую системами с открытым ключом.





















