Особенности расчёта цепей, содержащих операционные усилители

Лекция № 7

Особенности расчёта цепей , содержащих операционные усилители.

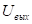
Питание по постоянному току не указывается. Используем упрощение модели. Будем использовать простую модель.

                                                                    

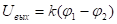
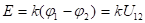
Входное сопротивление = ∞, выходное сопротивление = 0.

- инвертируемый потенциал.

Рекомендуемые материалы

- инвертирующий потенциал.

Для итерационных цепей, усилительный коэффициент деления К обычно очень большой, от нескольких тысяч до нескольких миллионов. Поэтому можно считать, что этот коэффициент .

Но 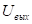- конечная величина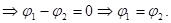

Т.о. нужно рассчитать в общем виде, а потом вывести , что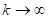

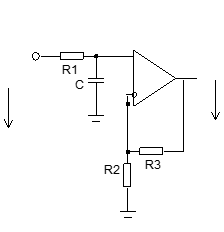
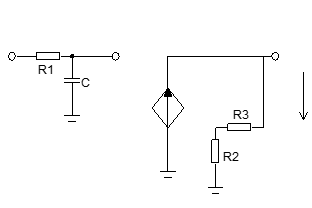
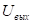
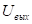
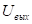
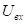
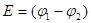
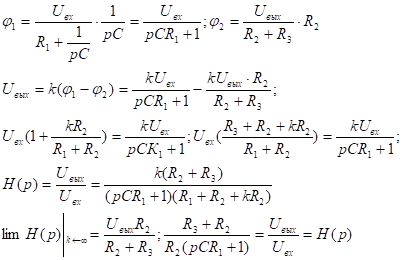
Нахождение реакции цепи на воздействие произвольной формы с помощью переходной и импульсной характеристики.

                                              

         

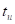
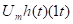
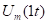
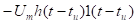
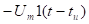
Будем решать эту задачу методом наложения. Найдём реакции на каждый скачок в отдельности, а потом всё сложим.

                                               

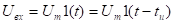
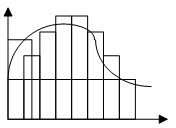
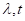
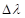
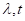
Каждый скачек

- интеграл Дюамеля.

Т.о. нахождение реакции цепи следующие:

1) Находим

2)Вычисляем интеграл Дюамеля

Если входные функции имеют скачки не только при t =0, то эти скачки в интеграле Дюанеля должны быть учтены отдельно.

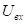
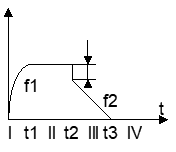
                                                          0 < t <t₁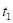

                                                         

                                                         

.   

   

                                       

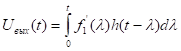
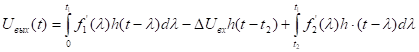
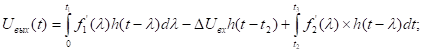
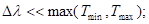
Возьмём  чтобы каждый прямоугольник считать импульсным воздействием.

                                                                       

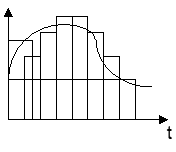
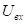
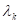
Напряжение на выходе будет равно сумме реакции скачков.

      интеграл свёртки.

Из математики известно:

1.Вычислим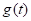

2. Вычислим интеграл свёртки.

Прохождение прямоугольного импульса через RC.

                                                                               

                                                                   

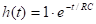
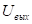
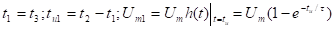
В результате прохождения R и C изменим амплитуду и его длительность и импульс запаздывает.

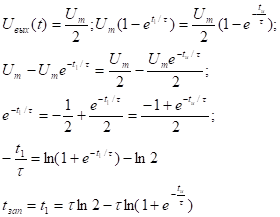
 время запаздывания

Лекция № 8

Найдём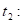 

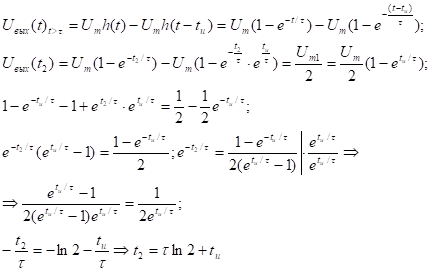
Теперь можно найти :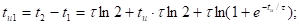

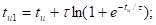
Амплитуда импульса на выходе меньше чем на входе. Импульс на выходе запаздывает, чем на входе. И длительность импульса на выходе больше чем на входе.

Рассмотрим эту ситуацию для частных случаев.

1) импульс длинный;

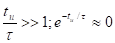
Тогда:

Если импульс достаточно длинный, то длительность и амплитуда не меняется, а импульс запаздывает на величину 2ln 2

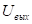
2)

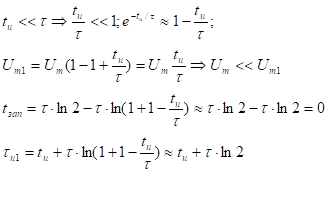
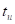-длительность импульса на входе;

 длительность импульса на выходе

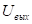                                                              Если схема работает в таком режиме, его

                                                              Называют расширяющий режим.

Рассмотрим вторую RC  - цепь:

                                                      

                                            

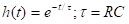
 Импульс на выходе – вершина уменьшается по экспоненте; после окончания импульса на входе возникает отрицательный экспоненциальный импульс.

Пусть

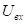
Пусть

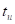
Использование RC – цепи в качестве фильтра верхних частот и дифференцирующих.

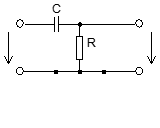
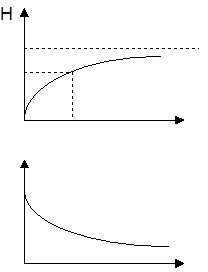
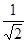
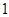
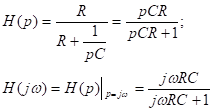
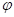
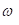
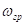
АЧХ

ФЧХ

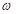
Частотная характеристика такого вида – это фильтр верхних частот. Верхние частоты проходят без искажений, а низкие частоты подавляются. Высокие частоты проходят без фазового сдвига, низкие имеют большой фазовый сдвиг.

Введём понятие граничной частоты:

 возведём в квадрат:

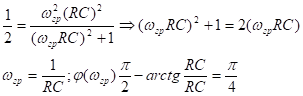
Это цепочка RC часто используется в качестве разделительного фильтра.

Пусть напряжение на входе:

 тогда:

Пусть1-я гармоника:  

Тогда: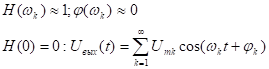

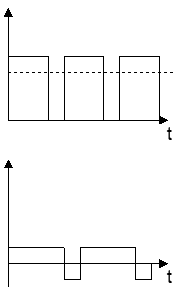
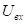
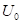
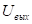
Рассмотрим следующую ситуацию:

Пусть: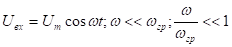

Выражение: перепишем в следующем виде:

А умножение на p означает дифференцирование:

 в таком случае наша цепь делает дифференцирование:

Т.о в частотной области сигнал дифференцируется, но амплитуда сигнала на выходе <<амплитуды сигнала на входе. Чем лучше выполняется условие дифференцирования, тем меньше амплитуда.

Рассмотрим условия дифференцирования во временной области.

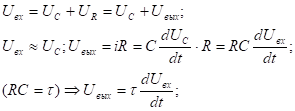
Если  то:   или

 условие, при котором цепь можно считать дифференцирующей.

Рассмотрим сигнал (будет л.р.):

                                               

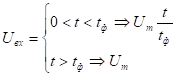
                                               время фронта

                                               

                                                          

                                               

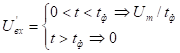
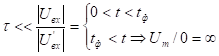
На первом интервале для любых  найдётся такой интеграл времени, для которого условия дифференцирования не выполняются.

Для второго интервала условие дифференцирования выполняется для любых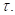

Нужны дополнительные исследования.

Лекция № 9

                                   - график в прошлой лекции

Дополнительные исследования: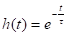

                                                   

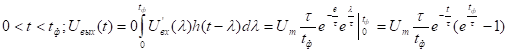
                                                      (форма сигнала будет приближаться к

                                                        производной )

Рассмотрим влияние сопротивления генератора и нагрузки на дифференцирующие свойства цепи.

Нагрузка.

                                         

 Пусть генератор школьный, а нагрузку заменим

                                                                               сопротивлением нагрузки.

                                                                                         

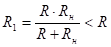
Проанализируем ситуацию в частотной области:

             Условие дифференцирования: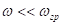

Т.к. за счёт нагрузки 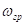 увеличилась, условия дифференцирования будут выполняться лучше, т.е. дифференцирование (операция) будет выполнятся точнее.

 амплитуда уменьшается (сигнал на выходе усиливается)

Сопротивление генератора.

                                           Рассмотрим в частотной области:

                                             

Т.к. 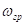стала меньше, то качество дифференцирования стало хуже.

Найдём напряжение на выходе (в частотной области)

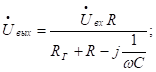
Т.е.  в первом приближении остаётся таким же. Тогда: амплитуда такая же, как на входе, а точность дифференцирования ухудшилась.

Но  должно увеличиваться, но этого не происходит. (Разобраться, почему?)

Использование RC цепи в качестве фильтра нижних частот и интегрирование.

                                                   

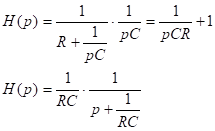
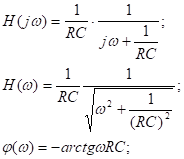
Цепь с такими ЧХ называют фильтром нижних частот (ФНЧ).

Сигналы низких частот проходят с небольшим искажением, а сигналы с высокими частотами подавляются очень сильно.

Если  и если выбрать цепь такую, что , то

(т.е.на выходе будет присутствовать только постоянная составляющая) и она часто используется в схемотехнике для того, чтобы исключить влияние отдельных каскадов в схеме друг на друга.

Для цифровых микросхем часто используется сопротивление самих проводников.

Использование RC цепи в качестве интегрирующей.

Рассмотрим в частотной области:

  Обозначим: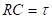

 т.к.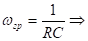

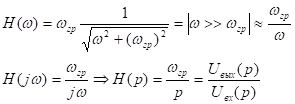
   (деление на p в изображении означает интегрирование во временной области)

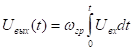
Пусть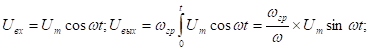

 (чем точнее условие интегрирования, тем меньше амплитуда).

Интегрирование во временной области:

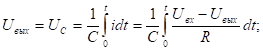
поэтому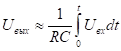

     - Условие дифференцирования

                                                  

                                      

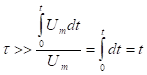
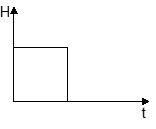
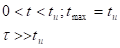
Дополнительное исследование:

 (вывести)

                                                          

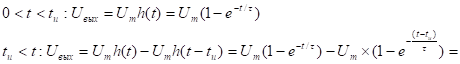
                                                                      Нужно задать ещё одно условие: в течении

                                                           какого времени после прохождения импульса  

                                                           должно быть близко к постоянному значению.

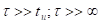
        Влияние сопротивления генератора и нагрузки (самостоятельно).

Цепи с распределёнными параметрами  (или длинные линии).

                                                       Генератор и нагрузка соединены проводами.

В частотной области линия считается длинной, если не выполняется условие где  - это длина волны.

Вместе с этой лекцией читают "ТЕМА 4. Государственные нормативные требования по охране труда".

Во временной области линия считается длинной, если время распространения сигнала вдоль неё сопоставимо с длительностью процессов в схеме и влияет на работу системы в целом.

Мы будем рассматривать однородные линии, которые имеют одинаковое поперечное сечение по всей длине.

Линия характеризуется распределёнными параметрами.

Уравнение длинной линии.

Для составления уравнений разобьём линию на отрезки, которые  и в пределах каждого такого отрезка заменим этот отрезок цепью с сосредоточенными параметрами.