Сигналы в электронных промышленных устройствах

2. СИГНАЛЫ В ЭЛЕКТРОННЫХ ПРОМЫШЛЕННЫХ УСТРОЙСТВАХ

Одно и то же сообщение может быть передано разными сигналами. Сигнал может быть электрическим, акустическим, оптическим — в зависимости от свойств источника, приемника и среды, в которой передается сообщение. Основное внимание будем уделять электрическим сигналам.

Так как сообщение предполагает изменение состояния источника, сигнал также должен иметь какой-то один или группу параметров, подвергающихся изменению. Сигнал, в котором ничего не меняется, не может нести информации. Показания прибора становятся информативными только при их изменении. Так, сейсмограф привлекает внимание лишь тогда, когда он после длительной паузы свидетельствует о толчке.

В зависимости от того, какой исходной (априорной) информацией о свойствах источника и характере протекания сигнала во времени мы располагаем, принято разделять сигналы на детерминированные и случайные.

Детерминированными считаются такие сигналы, поведение которых можно предсказать заранее с приемлемой точностью. В свою очередь, детерминированные сигналы делятся на периодические и непериодические. Наиболее распространенным примером периодического сигнала является гармоническое колебание. Допустим, что генератор вырабатывает синусоидальное напряжение с амплитудой U_m, частотой w₀ и начальной фазой j₀. Тогда мгновенное значение напряжения на выходе такого генератора в любой момент времени описывается выражением:

u(t) = U_m Sin(w₀t + j₀),

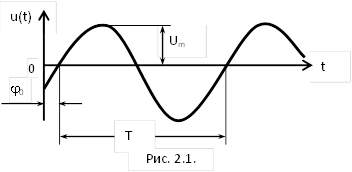где w₀ = 2p¤Т. Временная диаграмма такого сигнала представлена на рис.2.1.

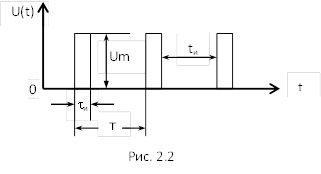Кроме гармонических колебаний, в качестве периодических сигналов могут быть использованы сигналы прямоугольной формы (рис.2.2). Сигналы прямоугольной формы характеризуются следующими параметрами: амплитудой импульса U_m, периодом Т длительностью импульса t_и  и длительностью паузы t_и. Такой сигнал также может быть описан математическим выражением.

Таким образом, любой детерминированный сигнал может быть задан своей математической моделью — описанием в виде некоторой, вполне определенной функции времени, что облегчает анализ различных свойств сигнала и способов его преобразования.

Рекомендуемые материалы

Случайными называют сигналы, которые, в отличие от детерминированных, нельзя предсказать с достаточно малой погрешностью.

Любой сигнал может быть представлен в двух математических формах – временной и частотной.

Представление сигнала во временной области позволяет определить такие его параметры, как форму, энергию, мощность и длительность.

Часто уделяется большое внимание изучению частотных свойств сигнала. Для этого используется представление сигнала в частотной области в виде спектра, получаемого на основе математического аппарата преобразования Фурье. Знание частотных свойств позволяет решать задачи идентификации характеристик сигнала (определения его наиболее информативных параметров), фильтрации (выделения полезного сигнала на фоне помех), выбора частоты дискретизации непрерывного сигнала. Одним из важнейших параметров сигнала является ширина его частотного спектра, так как именно этот параметр оказывается определяющим при согласовании сигнала с аппаратурой обработки и передачи информации. Полагая, что сигнал описывается известной функцией времени, т. е. является детерминированным, рассмотрим особенности получения и анализа частотных спектров.

Для гармонического сигнала u(t) = U_m Sin(w₀t + j₀)  амплитудный спектр представляется одной линией (рис.2.3).

Периодическая функция произвольного вида, удовлетворявшая условиям Дирихле, может быть представлена рядом

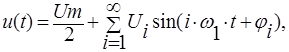
где U_m/2—постоянная составляющая, U_i, iw_i и j_i —соответственно амплитуда, угловая частота и начальная фаза i-й гармоники.

Амплитудный спектр периодического сигнала является линейчатым (дискретным) и гармоническим.

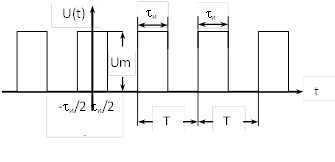Периодический импульсный сигнал, изображенный на рис.2.4, описывается выражением:                                 

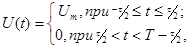
На рис. 2.5 приведен график амплитудного частотного спектра исследуемого сигнала для t_и/Т= 1/2 (по оси ординат отложены относительные значения амплитуд гармоник U_i/U_m).

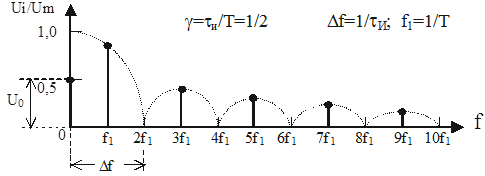Рис. 2.5.

Как видно из графика, в спектре сигнала преобладают низкочастотные составляющие. Нетрудно убедиться, что распределение средней мощности сигнала по его гармоникам является следующим: 50 %—постоянная составляющая, 40%— первая гармоника, 5 % — третья гармоника, 1 % - пятая гармоника. и т.д. Таким образом, в диапазоне частот (0 … 2f₁) содержится 90% средней мощности импульсного сигнала, в полосе частот (0 … 4f₁) — 95 % мощности сигнала.

Изменение соотношения между длительностью t_и и периодом Т следования импульсов приводит к перераспределению указанной мощности сигнала по отдельным участкам спектра — уменьшается удельный вес его низкочастотных составляющих, возрастает удельный вес высших гармоник. На рис. 6 показан график амплитудного частотного спектра для t_и/Т = 1/5.

Рис. 2.6.

Вычисления показывают, что 90 % средней мощности сигнала содержится в диапазоне частот (0 … 5f₁), а 95 % — в полосе (0 … 10f₁). Оценивая практическую (эффективную) ширину частотного спектра Df по 90% - ному содержанию мощности, можно воспользоваться следующей формулой (см. рис. 5 и рис. 6):, откуда видно, что Df определяется главным образом длительностью прямоугольного импульса t_и.

Частотный спектр непериодического сигнала формально можно получить из спектра соответствующего периодического сигнала, принимая Т®¥. В этом случае разность частот между двумя соседними гармониками f₁=1/Т стремится к нулю, т. е. частотный спектр из дискретного (линейчатого) становится непрерывным (сплошным).

"8. Автоколебательные процессы" - тут тоже много полезного для Вас.

На рис.2.7 приведен частотный спектр одиночного прямоугольного импульса, принимающего, значение U_m на интервале [-t/2, t/2].

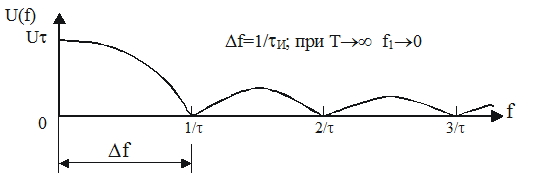
Рис. 2.7.

Как видно на рис. 7, энергия исследуемого сигнала также в основном сосредоточена в области низких частот (90% полной энергии сигнала содержится в диапазоне частот от 0 до f=1/t_и; 95 % — в диапазоне частот, не превышающих f=2/t_и). Таким образом, как и в случае периодического импульсного сигнала (см. рис. 4), здесь можно говорить о практической ширине  частотного спектра Df, которая влияет на поведение (форму) сигнала.Если принять, что полоса частот Df содержит 90% энергии сигнала, то получаем Df=1/t_и. Иногда последнее выражение записывают так:

t_и´Df = 1

и называют его соотношением неопределенностей. Как видно из этого соотношения, чем короче импульс (меньше t_и), тем более широкий спектр должен быть сохранен при передаче сигнала, например, по линии связи. Удлинение импульса позволяет обойтись узкополосной линией связи для передачи значительной части энергии сигнала. Для рассмотренного ранее периодического импульсного сигнала полоса частот Df, подсчитываемая по 90 %-ному содержанию мощности, также принимает значение, равное 1/t_и.На практике периодический сигнал в электрической цепи можно получить, если генератор сигналов работает достаточно долго.