Вырожденные типы направленных систем
Лекция 7
2.3 Вырожденные типы направленных систем
Выходные переменные направленной системы также могут влиять на ее входные переменные, но это влияние, если оно имеет место, осуществляется не через систему, а, как это показано на рис. 2.2,а, через среду.
Существует два типа вырожденных направленных систем.
1. Направленные системы без выходных переменных (рис. 2.2,б), т е. системы с  . Эти системы методологически бесполезны. В самом деле, любая такая система имеет только входные переменные, которые по определению полностью задаются средой, и, следовательно, их свойства невозможно представить и исследовать внутри самой системы. Таким образом, в системе нечего описывать и изучать любое утверждение, которое можно сформулировать внутри системы, бессмысленно, так как оно содержит только условие, но не следствие. Следовательно, для п переменных имеется только
. Эти системы методологически бесполезны. В самом деле, любая такая система имеет только входные переменные, которые по определению полностью задаются средой, и, следовательно, их свойства невозможно представить и исследовать внутри самой системы. Таким образом, в системе нечего описывать и изучать любое утверждение, которое можно сформулировать внутри системы, бессмысленно, так как оно содержит только условие, но не следствие. Следовательно, для п переменных имеется только  осмысленных объявлений входа-выхода.
осмысленных объявлений входа-выхода.
2. Направленные системы без входных переменных (рис. 2.2,в), т. е. системы с  .Эти системы методологически интересны, поскольку для них можно сформулировать содержательные утверждения. Однако эти утверждения не могут быть условными, поскольку в таких системах нет входных переменных, на которых можно было бы сформулировать эти условия.
.Эти системы методологически интересны, поскольку для них можно сформулировать содержательные утверждения. Однако эти утверждения не могут быть условными, поскольку в таких системах нет входных переменных, на которых можно было бы сформулировать эти условия.

а) б)
Рекомендуемые материалы
в) г)
Рис.2.2. Методологические отличия направленных и нейтральных исходных систем.
Для нейтральных систем никакой среды нет (рис. 2.2,г). При замене нейтральной системы на направленную вводится среда, и если  , некая информация, содержавшаяся в системе, перемещается в среду. Таким образом, полученная направленная система содержит меньше информации, чем исходная нейтральная.
, некая информация, содержавшаяся в системе, перемещается в среду. Таким образом, полученная направленная система содержит меньше информации, чем исходная нейтральная.
Отличия между нейтральными и направленными системами и между четкими и нечеткими каналами наблюдения — это еще два методологических отличия исходных систем. Любая исходная система является или нейтральной, или направленной, а каналы наблюдения ее переменных или все четкие, или все нечеткие, или разных типов. Таким образом, новые отличия дают 2х3=6 возможностей. Кроме того, в исходную систему могут входить переменные разных методологических типов. Обозначим общее число методологических отличий, определенных для уровня исходных систем, через #S. Тогда при вполне разумном предположении, что число параметров не превышает 9  , мы получим
, мы получим
 , (2.13)
, (2.13)
где  .
.
Методологические отличия, определенные для исходных систем, весьма важны, поскольку они могут быть применены и ко всем системам более высоких типов.
Пример 2.1. Пусть объектом исследования являются некоторый вычислительный центр, осуществляющий распределенные вычисления. Каждый элемент данного вычислительного центра характеризуется определенными свойствами. Предположим, что качественные показатели некой вычислительной процедуры зависят от набора задействованных вычислительных средств из заданного комплекса. Для текущих вычислений используются элементы, являющиеся оптимальными с точки зрения специально подготовленного обслуживающего персонала.
Цель определения исходной системы для данного объекта — получение характеристик комплекса в целом, их оценка и разработка более подходящих и точных руководств для наилучшего использования вычислительных средств. Базой в данном примере является группа элементов, способных осуществлять некоторые операции с данными. Пусть каждый исследуемый элемент помечается целым числом. Тогда функция  дает отображение «один в один», равно как и функция
дает отображение «один в один», равно как и функция  .
.
Пусть для исследования объекта было отобрано четыре свойства. Приведем их описания и определим соответствующие переменные.
Совокупность (множество) элементов, на которые возложены функции контроля вычислительных операций: свойство  . Для исследования в данном вычислительном комплексе, выделено только четыре класса множеств. Следовательно, для представления этого свойства нужна конкретная переменная с четырьмя состояниями. На рис. 2.3,а определена функция
. Для исследования в данном вычислительном комплексе, выделено только четыре класса множеств. Следовательно, для представления этого свойства нужна конкретная переменная с четырьмя состояниями. На рис. 2.3,а определена функция  , связывающая свойство с этой переменной. На том же рисунке определяется функция
, связывающая свойство с этой переменной. На том же рисунке определяется функция  , которая, как всегда, представляет собой простую схему переобозначения. Множества
, которая, как всегда, представляет собой простую схему переобозначения. Множества  и
и  никакими свойствами не обладают, и, следовательно, всевозможные свойства целых чисел из множества
никакими свойствами не обладают, и, следовательно, всевозможные свойства целых чисел из множества  не могут быть использованы. Канал наблюдения является четким, т. е. непосредственно представляется функцией
не могут быть использованы. Канал наблюдения является четким, т. е. непосредственно представляется функцией  .
.
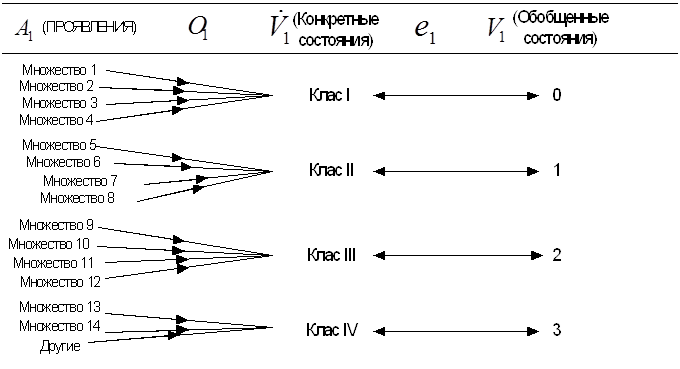
Рис. 2.3, а. Определение переменных для признаков  .
.
Максимально возможная эффективность элементарных вычислительных операций (в относительных единицах): свойство  . Предположим, что для данного представления достаточно дать качественную характеристику, то есть разбить количественный критерий всего на пять категорий. Они определяются на рис. 2.3,б вместе с функциями
. Предположим, что для данного представления достаточно дать качественную характеристику, то есть разбить количественный критерий всего на пять категорий. Они определяются на рис. 2.3,б вместе с функциями  и
и  . Несмотря на то, что возле границ блоков разбиения
. Несмотря на то, что возле границ блоков разбиения  может иметь место некоторая нечеткость измерения, канал наблюдения о2 можно рассматривать как четкий, так как эта нечеткость для данного исследования не существенна. Множества
может иметь место некоторая нечеткость измерения, канал наблюдения о2 можно рассматривать как четкий, так как эта нечеткость для данного исследования не существенна. Множества  можно рассматривать как линейно упорядоченные с метрическим расстоянием, и, следовательно, если нужно, то можно для множества
можно рассматривать как линейно упорядоченные с метрическим расстоянием, и, следовательно, если нужно, то можно для множества  воспользоваться свойствами целых чисел.
воспользоваться свойствами целых чисел.
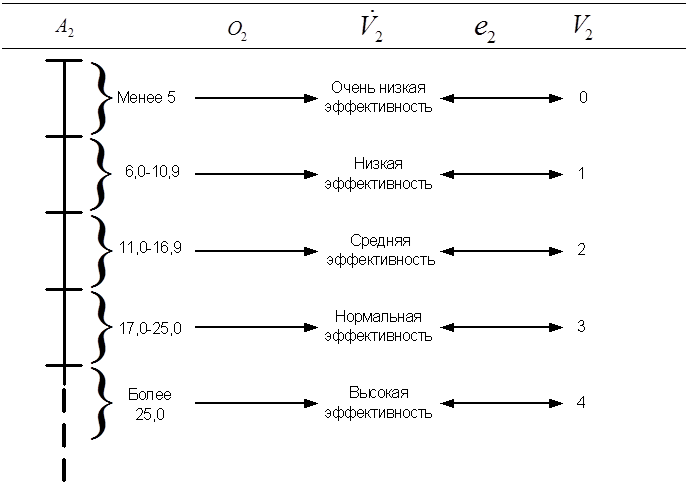
Рис. 2.3, б. Определение переменных для признаков  .
.
Загруженность центра в целом: свойство  . Оценивается при помощи некоторых количественных характеристик. Однако в данном рассмотрении предполагается некоторая неточность, полученных оценок. То есть нечеткий канал наблюдения. Множество
. Оценивается при помощи некоторых количественных характеристик. Однако в данном рассмотрении предполагается некоторая неточность, полученных оценок. То есть нечеткий канал наблюдения. Множество  обладает свойством линейной упорядоченности с метрическим расстоянием.
обладает свойством линейной упорядоченности с метрическим расстоянием.
Эффективность центра для данной вычислительной процедуры: свойство  . Получается на базе научной подготовки обслуживающего персонала. Свойство предполагает только два состояния. То есть либо истинность, либо его ложность. Множество
. Получается на базе научной подготовки обслуживающего персонала. Свойство предполагает только два состояния. То есть либо истинность, либо его ложность. Множество  никакими свойствами не обладает.
никакими свойствами не обладает.
Мы видим, что определенная в этом примере исходная система является нейтральной. Однако для формулирования правил оптимального использования вычислительных средств, система должна быть переопределена как направленная с входными переменными  и выходной переменной и
и выходной переменной и  . Один канал наблюдения нечеткий, а остальные четкие, поэтому в исходной системе смешаны четкие и нечеткие переменные. Множество параметров свойствами не обладает, а множества состояний имеют два, а, возможно, и три типа: без свойств, линейно упорядоченные и, линейно упорядоченные с метрическим расстоянием.
. Один канал наблюдения нечеткий, а остальные четкие, поэтому в исходной системе смешаны четкие и нечеткие переменные. Множество параметров свойствами не обладает, а множества состояний имеют два, а, возможно, и три типа: без свойств, линейно упорядоченные и, линейно упорядоченные с метрическим расстоянием.
Алгоритм формализации представляющих систем
- Определяются vi, Vi,
![]() означающие соответственно обобщенную переменную, ее множество состояний и множество математических свойств, определенных для нее.
означающие соответственно обобщенную переменную, ее множество состояний и множество математических свойств, определенных для нее. - Определяются
![]() ,
, ![]() ,
, ![]() те же характеристики конкретной переменной, являющиеся конкретизацией переменной vi .
те же характеристики конкретной переменной, являющиеся конкретизацией переменной vi . - Определяются
![]() и
и ![]() соответственно обобщенный параметр, его множество состояний и множество математических свойств, определенных на параметре wj.
соответственно обобщенный параметр, его множество состояний и множество математических свойств, определенных на параметре wj. - Определяются
![]() и
и ![]() — те же характеристики конкретного параметра, полученные конкретизацией параметра wj.
— те же характеристики конкретного параметра, полученные конкретизацией параметра wj. - Определяются
![]() и
и ![]() — соответственно конкретная и общая представляющая системы:
— соответственно конкретная и общая представляющая системы: ![]()
![]() .
.
Для направленных систем, дополнительно
1. Определяется  , если
, если  или,
или,  то это значит, что переменная
то это значит, что переменная  является соответственно входной или выходной.
является соответственно входной или выходной.
Бесплатная лекция: "Диагностика внематочной беременности (ВБ)" также доступна.
2. Направленные аналоги нейтральных систем: 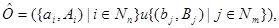
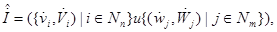
 .
.
Алгоритм формализации исходных систем
- Определяется канал наблюдения, с помощью которого свойство ai представляется переменной
![]() : Oi : Ai→
: Oi : Ai→ ![]() .
. - Определяется представление базы bj, параметром
![]() : ωj : Bj →
: ωj : Bj → ![]() .
. - Определяется функция ei , конкретизирующая обобщенную переменную vi , изоморфная относительно математических свойств
![]() : ei : Vi→
: ei : Vi→ ![]() .
. - Определяется функция εj , конкретизирующая обобщенный параметр wj , изоморфная относительно математических свойств
![]() : εj : Wj →
: εj : Wj → ![]() .
. - Определяется четкий полный канал наблюдения:
![]() должны быть гомоморфны относительно свойств
должны быть гомоморфны относительно свойств ![]() и
и ![]() }, {(
}, {(![]() ,
,![]() ,
,![]() должны быть гомоморфны относительно свойств
должны быть гомоморфны относительно свойств ![]() и
и ![]() }).
}). - Определяется каналом конкретизации абстрагирования:
![]() должны быть изоморфны относительно свойств
должны быть изоморфны относительно свойств ![]() и
и ![]() },
}, ![]() должны быть изоморфны относительно свойств
должны быть изоморфны относительно свойств ![]() .
. - Определяется исходная система:
![]() . Для направленных систем
. Для направленных систем ![]() .
.
К.Р. № 7
Приведите подробный пример вырожденной системы.



 означающие соответственно обобщенную переменную, ее множество состояний и множество математических свойств, определенных для нее.
означающие соответственно обобщенную переменную, ее множество состояний и множество математических свойств, определенных для нее. ,
,  ,
,  те же характеристики конкретной переменной, являющиеся конкретизацией переменной vi .
те же характеристики конкретной переменной, являющиеся конкретизацией переменной vi . и
и  соответственно обобщенный параметр, его множество состояний и множество математических свойств, определенных на параметре wj.
соответственно обобщенный параметр, его множество состояний и множество математических свойств, определенных на параметре wj. и
и  — те же характеристики конкретного параметра, полученные конкретизацией параметра wj.
— те же характеристики конкретного параметра, полученные конкретизацией параметра wj. и
и  — соответственно конкретная и общая представляющая системы:
— соответственно конкретная и общая представляющая системы: 
 .
. : ωj : Bj →
: ωj : Bj →  .
. должны быть гомоморфны относительно свойств
должны быть гомоморфны относительно свойств  и
и  }, {(
}, {( ,
, ,
, должны быть гомоморфны относительно свойств
должны быть гомоморфны относительно свойств  }).
}). должны быть изоморфны относительно свойств
должны быть изоморфны относительно свойств  },
},  должны быть изоморфны относительно свойств
должны быть изоморфны относительно свойств  .
. . Для направленных систем
. Для направленных систем  .
.


















