Лекция 5

Лекция 5.

План:

1. Сжимаемость жидкости.

2. Число Маха.

§2.5.1. Сжимаемость жидкости.

Сжимаемость — это свойство жидкостей изменять плотность (объем) при изменении давления и температуры. Для количественной оценки сжимаемости используется модуль упругости жидкостей  — отношение изменения давления  к относитель­ному изменению плотности  (Па) в данном процессе

                                                          (2.22)

Относительное изменение плотности при заданном изменении давления  обратно пропорционально модулю упругости. Капельные жидкости малосжимаемы и их модули упругости достаточно велики. Для воды, керосина и ртути соответственно – .

При изменении температуры плотность жидкости изменяется более существенно. Это свойство используется в термометрах и термостатах.

Рекомендуемые материалы

Сжимаемость газов очень велика. Переходя от конечных раз­ностей к дифференциалам, получим

                                                          (2.23)

При изотермическом процессе   т. е. сжимаемость газов тем больше, чем меньше давление.

При изоэнтропном процессе  и

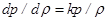
                                                                               (2.24)

и сжимаемость газов определяется не только давлением, но и показателем изоэнтропы , уменьшаясь с его увеличением. В этом: проявляется влияние изменения температуры на изменение плотности газа в изоэнтропном процессе.

Для количественной оценки сжимаемости жидкости при изменении только температуры при  используется коэффициент температурного расширения . Учет изменения плотности газа, вызванного изменением температуры, имеет осо­бенно существенное значение при исследовании пограничного слоя.

Несжимаемая жидкость — жидкость, плотность которой при изменении давления и температуры не изменяется (). Эта модель используется для упрощения исследования течений, когда относительное изменение плотности жидкости весьма мало. Для решения вопроса — применима ли модель несжимаемой жидкости при исследовании заданного течения — необходимо знать изменения давления и температуры и вызванное ими относительное изменение плотности. Изменение давления в потоке несжимаемой жидкости без обмена энергией с внешней средой и без потерь определим, используя известное из курса физики уравнение Бернулли

                                                      (2.25)

Из уравнения следует, что, в заданных условиях полная энергия жидкости постоянна, а ее составляющие — потенциальная энергия давления и кинематическая энергия могут взаимопревращаться. Предположив, что в процессе скорость течения может только уменьшаться, придем к выводу, что максимально возможное изменение давления в процессе течения будет равно скоростному напору .

Свяжем воедино характеристику процесса , характеристику жидкости  и допустимую погрешность в пренебрежении сжимаемостью (). Получим критерий, определяющий предел применения модели несжимаемой жидкости

                                 (2.26)

Итак, газ можно рассматривать как несжимаемую жидкость, если скоростной напор существенно меньше модуля объемной упругости. Знак приблизительно равно в (2.26) отражает использование уравнения Бернулли для несжимаемого газа, что, однако, при ре­шении задачи о пределе применения модели несжимаемой жидко­сти не вызывает ощутимой погрешности.

Скорость звука 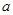, м/с — скорость распространения малых возмущений давления в данной среде, рассчитывается по формуле, известной из курса физики, а также с учетом (2.23)

                                                (2.27)

Для совершенного газа, с учетом адиабатического процесса, в звуковой волне (; 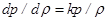) и уравнения состояния, получим из (2.27):

                                          (2.28)

В несжимаемых средах  и , т.е. возмущения распространяются мгновенно. Все жидкости в большей или меньшей степени сжимаемы и звук в них распространяется с конечными скоростями.

Скорость звука в данном газе зависит только от его абсолютной температуры —. Скорость звука в различных газах при одинаковой температуре зависит от их природы . Показатель изоэнтропы для различных газов изменяется в узких пределах (), поэтому основное влияние оказывает молекулярная масса газа.

§2.5.2. Число Маха.

Число Маха — отношение скорости газа  к местной скорости звука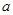

                                                                                            (2.29)

На практике часто используется число Маха  полета, что правомерно, так как в соответствии с принципом относительности движения .

Подставляя в (2.26) значение модуля упругости из (2.27) и используя (2.29), получим условие, когда газ можно считать несжимаемым

                                                                        (2.30)

Число Маха в газовой динамике является важнейшим критерием сжимаемости движущегося газа. Газ можно рассматривать как несжимаемую жидкость только при течениях с (обычно при ).

Если Вам понравилась эта лекция, то понравится и эта - 54. Классификация пожароопасных и взрывоопасных зон.

Молекулярные теплопроводность и диффузия. При существовании поперечных градиентов температуры  и концентрации , кг/м³ избыточной примеси  в жидкости наблюдается теплопроводность и диффузия. Удельные потоки тепла , Дж/(м²-с) и избыточной примеси G, кг/(м²-с) определяются законами Фурье и Фика

                                                 (2.31)

Коэффициенты теплопроводности , Дж/(м-с-К), температуропроводности , м²/с и диффузии , м²/с для газов определяются теоретически в кинетической теории газов

                              (2.32)

Формулы (2.31) и (2.32) имеют одинаковую структуру с (2.10), (2.12) и (2.13). Это является результатом того, что механизм молекулярного переноса количества движения (трения), тепла (теплопроводности) и вещества (диффузия) в газах одинаков — тепловое хаотическое движение молекул.

Для капельных жидкостей величины этих коэффициентов определяются экспериментально.