💯Высшая математика Темы 1-17 / Самый полный сборник из 290 правильных ответов на отлично! 100/100
Ответы к экзамену: Высшая математика Темы 1-17 вариант Темы 1-17
Описание
🌞Важно!. Информация по изучению курса
Тема 1. Функция. Способы задания. Неявная функция. Обратная функция. Классификация функций
Тема 2. Теория пределов
Тема 3. Предел функции. Непрерывность функции. Разрыв функции. Основные свойства непрерывных функций
Тема 4. Замечательные пределы. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины
Тема 5. Дифференцирование функций. Часть 1
Тема 6. Дифференцирование функций. Часть 2
Тема 7. Дифференциал функции. Производные и дифференциалы высших порядков
Тема 8. Аналитические приложения дифференцируемых функций
Тема 9. Экстремум функции
Тема 10. Неопределенный интеграл. Основные свойства. Таблица неопределенных интегралов. Метод непосредственного интегрирования
Тема 11. Неопределенный интеграл. Основные методы интегрирования
Тема 12. Определенный интеграл. Определенный интеграл. Задачи, приводящие к понятию определенного интеграла
Тема 13. Приложения определенного интеграла
Тема 14. Основы линейной алгебры. Матрицы. Виды матриц. Операции над матрицами
Тема 15. Теория определителей. Основные свойства определителей. Вычисление определителей произвольного порядка n. Формулы разложения
Тема 16. Обратная матрица. Ранг матрицы. Понятие обратной матрицы
Тема 17. Системы линейных алгебраических уравнений
Абсциссами точек перегиба графика функции y = x³ / 6 − x² / 2 являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
3
4
Абсциссами точек перегиба графика функции y = x³ являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2
3
0
4
Боковые стороны и меньшее основание трапеции равны по 10 см. Определить ее большее основание так, чтобы площадь трапеции была наибольшей.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
13 см
15 см
22 см
20 см
25 см
Вертикальными асимптотами графика функции y = lnx являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
х = е
х = 0
х = 1
х = –1
∅
Выберите правильный ответ на вопрос: производная [c ⋅ u(x) - d ⋅ v(x)]'], гдеси d —действительныечисла, равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
c' ⋅ u(x) − d' ⋅ v(x)
c ⋅ u'(x) + d ⋅ v'(x)
c ⋅ u'(x) − d ⋅ v'(x)
c ⋅ u'(x) − d ⋅ v(x)
0
Выберите правильный ответ на вопрос: производная [u(x) ⋅ v(x)]' равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
u'(x) ⋅ v(x)
u(x) ⋅ v'(x)
u'(x) ⋅ v'(x)
u'(x) + v'(x)
u'(x)v(x) + u(x)v'(x)
Выберите правильный ответ на вопрос. Производная функции [u(x) / c]', где с — действительное число, равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
u'(x) / c'
cu'(x)
−u'(x) / c
u'(x) / c
u'(x) / c²
Вычислить ∫ √(4 − 5x)dx, x=−12..−1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
54 2/3
18 1/3
64 2/3
15
10
Вычислить ∫ dx / (a² + x²), x=a..a√3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
π / 2a
π / 3a
π / 12a
π / 4a
π / 6a
Вычислить ∫ dx / (x² + 6x + 8), x=2..8
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2 ⋅ ln(5/4)
ln(5/4)
3/4 ⋅ ln(5/4)
3 ⋅ ln(5/4)
2ln3
Вычислить ∫ dx / √(x² + 1), x=0..1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 + √2
ln2 + 1
2 ⋅ ln│1 + √2│
3 ⋅ ln│1 + √2│
ln│1 + √2│
Вычислить ∫ e^(x/3)dx, x=0..3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
е –1
2(e + 1)
2(e - 1)
3(e - 1)
1/2 ⋅ (e - 1)
Вычислить ∫ sin2xdx, x=0..π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
0
2
3/2
1/2
Вычислить ∫ sin4xdx, x=0..π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
1/3
2
1/2
Вычислить ∫ x³dx, x=1..3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
10
15
-20
-10
20
Вычислить ∫ xe^(x²)dx, x=0..1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
е –1
2е –1
3е +1
(e + 1) / 2
(e − 1) / 2
Вычислить ∫ xeˣdx, x=0..1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
2
1
3
4
Вычислить приближенно приращение функции y = x² + 2x + 3 когда х изменяется от 2 до 1,98.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,3
–0,5
0,01
–0,12
0,05
Геометрически первая производная от функции, если она существует, есть
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Синус угла наклона касательной к оси ОХ
Косинус угла наклона касательной к оси ОХ
Тангенс угла наклона касательной к оси ОХ
Котангенс угла наклона касательной к оси ОХ
Дифференциал функции y = sin²2x равен
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2 sin 2 xdx
2 cos2 xdx
–2 sin 2 xdx
sin 4 xdx
2 sin 4 xdx
Дифференциал функции y = x³ + 3x² + 3x равен
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(6x⁴ + 3x³ + 3x³)dx
(3x² + 6x + 3)dx
(3x² + 6x)dx
(x⁴ / 4 + x³ + 3 ⋅ x² / 2)dx
(x⁴ + 3x + 3)dx
Достаточными условиями существования производной непрерывной функции в точке являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Существование хотя бы одной односторонней производной
Существование двух односторонних производных
Существование и равенство двух односторонних производных
Заменив приращение функции дифференциалом, приближенно найти arctg 1,05.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,75
0,69
0,81
0,80
0,65
Заменив приращение функции дифференциалом, приближенно найти sin 31°.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,500
0,451
0,35
0,515
0,491
Из непрерывности функции
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
следует ее дифференцируемость
еще не следует ее дифференцируемость
следует разрывность первой производной
следует непрерывность первой производной
Какая из заданных функций задана явно:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
ху = 5;
x² + y² = 9;
у = sinx;
eˣʸ = 3;
lg(x + y) = 5.
Какая из заданных функций является обратной для функции Y=5x-3:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x = (y − 3) / 5;
x = (y + 3) / 5;
x = (5y − 3) / 5;
x = (3y − 5) / 5;
x = (3y + 5) / 5.
Какая из заданных функций является четной:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
y = x² - x;
y = x⁴ - 2x²;
y = x⁴ - x²;
y = x + 2;
y = x.
Касательная к графику функции y = x² в точке M₀(1; 1) определяется уравнением
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = х + 1
у = 2х – 1
у = 2х + 1
у = х –1
у = 2х + 3
Наибольшим значением функции y = x² − 2x на отрезке [–1; 1] является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
-1
3
5
∞
10
Найдите вторую производную заданной функции y = x / (x − 1)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
−1 / (x − 1)²
−1 / (x − 1)³
1 / (x − 1)⁴
2 / (x − 1)³
−2 / (x − 1)³
Найдите вторую производную функции у = sin2x.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2 sin 2x
4 cos 2x
– 4sin 2x
4 sin 2x
cos 2x
Найти все точки разрыва функции y = (2x - 1) / (x² - 8x + 15)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2
2 и 6
1 и 2
3 и 5
1 и 4
Найти интеграл ∫ ((√x - 1)² / x)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x√x − 2√x + ln|x| + c
x − 4√x + ln|x| + c
√x − 4x + ln|x| + c
√x − 2√x + ln|x| + c
x + 2√x + ln|x| + c
Найти интеграл ∫ ((10x⁵ + 5) / x³ )dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
10x³ + x² + c
10x² + x + c
10 / 3 ⋅ x³ - 5 / (2x²) + c
10 / 3 ⋅ x² - 5 / (2x) + c
10 / 3 ⋅ x - 5 / (2x) + c
Найти интеграл ∫ (√x + ∛x)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x√x + x∛x + c
2/3 ⋅ x√x − 3/4 ⋅ x∛x + c
2 ⋅ x√x + 3 ⋅ x∛x + c
3/2 ⋅ x√x + 4/3 ⋅ x∛x + c
2/3 ⋅ x√x + 3/4 ⋅ x∛x + c
Найти интеграл ∫ (2 / (1 + x²) − 3 / √(1 − x²))dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2 ⋅ arctgx − 3 ⋅ arcsinx + c
1/2 ⋅ arctgx + arcsinx + c
2 ⋅ arctgx − arccosx + c
2 ⋅ arcsinx − 3 ⋅ arctgx + c
2 ⋅ arccosx + 3 ⋅ arctgx + c
Найти интеграл ∫ (4 − 3x)e⁻²ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x / 4 ⋅ e⁻²ˣ + C
(2x − 3) / 4 ⋅ e⁻²ˣ + C
3xe⁻²ˣ + C
(5 − 6x) / 4 ⋅ e⁻²ˣ + C
(6x − 5) / 4 ⋅ e⁻²ˣ + C
Найти интеграл ∫ ⁵√(x³)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/5 ⋅ x ⋅ ⁵√(x³) + c
5/8 ⋅ x ⋅ ⁵√(x³) + c
3/5 ⋅ x^(3/5) + c
−5/2 ⋅ x^(−2/5) + c
5/8 ⋅ x² ⋅ ⁵√(x³) + c
Найти интеграл ∫ aˣ(1 + a⁻ˣ / √(x³))dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из
нескольких предложенных вариантов
aˣ / lna − 3/2 ⋅ √x + c
aˣ / lna + 3/2 ⋅ √x + c
aˣ / lna − 3/2 ⋅ ∛x + c
aˣ / lna − 2/2 ⋅ ∛x + c
aˣ / lna + 3/2 ⋅ ∛x + c
Найти интеграл ∫ cos2xdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
-1/2 ⋅ sin2x + C
1/2 ⋅ sinx + C
cos²2x / 2 + C
1/2 ⋅ sin2x + C
sin2x + C
Найти интеграл ∫ dx / (√x + 1)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
ln│√x + 1│+ C
1/2 ⋅ ln│√x + 1│+ C
√x + 2ln│√x + 1│+ C
2√x − 2ln│√x + 1│+ C
2√x + 2ln│√x + 1│+ C
Найти интеграл ∫ cos²xdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
cos³x / 3 + c
1/2 ⋅ x + 1/4 ⋅ sin2x + c
1/2 ⋅ cos³x + c
x + sin2x + c
1/2 ⋅ x - 1/4 ⋅ sin2x + c
Найти интеграл ∫ dx / (x² + 6x + 13)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
arcsin(x + 3) + c
arcsin((x + 3) / 2) + c
arctg(x + 3) + c
1/2 ⋅ arctg((x + 3) / 2) + c
2arctg(x + 3) + c
Найти интеграл ∫ dx / √(4 − x²)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
arcsinx + c
arccosx + c
arcsin(x/2) + c
arctg(x/2) + c
1/2 ⋅ arctg(x/2) + c
Найти интеграл ∫ dx / √(x² + 3x)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2 ⋅ √(x² + 3x) + C
ln│x + 3/2 + √(x² + 3x)│+ C
2 ⋅ √(x² + 3x) + C
3 ⋅ ln│x + √(x² + 3x)│
ln│x + √(x² + 3x)│
Найти интеграл ∫ e⁵⁻³ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(5 - 3x)e⁵⁻³ˣ + C
−1/3 ⋅ e⁵⁻³ˣ + C
e⁵⁻³ˣ + C
1/3 ⋅ e⁵⁻³ˣ + C
e⁵⁻³ˣ ⋅ ln|5 − 3x| + C
Найти интеграл ∫ eˣdx / (e²ˣ − a²)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 / (2a) ⋅ ln│(eˣ − a) / (eˣ + a)│+ C
e²ˣ − a² + C
1 / a ⋅ (e²ˣ − a²)│+ C
1 / a ⋅ ln│e²ˣ − a²│+ C
1 / (2a) ⋅ ln│e²ˣ − a²│+ C
Найтиинтеграл ∫ x√(3 − 5x)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(5x + 2)√(3 - 5x) + C
(5x - 3)√(3 - 5x) + C
2/125 ⋅ (5x + 2)(5x - 3)√(3 - 5x) + C
(5x + 2)(5x - 3)√(3 - 5x) + C
(5x + 2)(5x + 3)√(3 - 5x) + C
Найти интеграл ∫ x²e⁻ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(x² + 2x + 2)e⁻ˣ + C
−(x² + 2x + 2)e⁻ˣ + C
(x² + 2)e⁻ˣ + C
(x² + 2x)e⁻ˣ + C
(x² − 2x + 2)e⁻ˣ + C
Найти интеграл ∫ x³dx / (x⁴ + 5)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
ln(x⁴ + 5) + c
4 ⋅ ln(x⁴ + 5) + c
1/4 ⋅ ln(x⁴ + 5) + c
−ln(x⁴ + 5) + c
−1/4 ⋅ ln(x⁴ + 5) + c
Найти интеграл ∫ xe⁻²ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x / 4 ⋅ e⁻²ˣ + C
−(2x +1) / 4 ⋅ e⁻²ˣ + C
(x +1) / 2 ⋅ e⁻²ˣ + C
(2x +1) / 4 ⋅ e⁻²ˣ + C
− x / 4 ⋅ e⁻²ˣ + C
Найти интервалы монотонного возрастания функции y = 6x² - 3x.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(−∞; 1/4);
(0; 1/4);
(−∞; 3)
(1/4; +∞);
(2; +∞).
Найти интервалы монотонного убывания функции y = x³ − 3x²
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(–2; 2);
(1; 2);
(–1; 1);
(0; 2);
(0; 3).
Найти объём тела, полученного от вращения плоской фигуры, ограниченной линиями y = sinx; x = π/2, y = 0 вокруг оси Ох.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из
нескольких предложенных вариантов
π² (куб. ед.);
π 2/4 (куб. ед.);
π (куб. ед.);
3/4 π² (куб. ед.);
2π (куб. ед.).
Найти площадь плоской фигуры, ограниченной линиями у = sinx, у = cosx, x = 0; x = π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
√2 (кв.ед.);
√2/2 (кв.ед.);
(√2 − 1) (кв.ед.);
3 (кв.ед.);
2 (кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями x = y² и у = –х + 2.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
4,5 (кв.ед.);
2,5 (кв.ед.);
3 (кв.ед.);
2 (кв.ед.);
3,5 (кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями y = √(lnx), y = 0, x = e вокруг оси Ох.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2π (куб. ед.);
3π (куб. ед.);
π (куб. ед.);
4π (куб. ед.);
5π (куб. ед.).
Найти площадь плоской фигуры, ограниченной линиями y = lnx, y = 0, x = e вокруг оси Ох.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2
3
e
5
Найти площадь плоской фигуры, ограниченной линиями y = x² - 2x + 1 у = 1.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3
4/3 (кв.ед.);
1/3 (кв.ед.);
5 (кв.ед.);
5/3 (кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями y = x² - 4x + 5; y = 5.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
8 2/3
10 2/3 (кв.ед.);
7 1/3 (кв.ед.);
10;
7 2/3(кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями y = x² - 9, у = 0.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
–36 кв.ед.;
18 кв.ед.;
54 кв.ед.;
36 кв.ед.;
26 кв.ед.
Найти предел на основании свойств пределов lim (4x³ − 2x² + 5x − 1), x⟶2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
26
33
18
Найти предел функции lim (3x² - 5x + 2), x⟶2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
2
4
22
1
Найти предел функции lim 2^(1 / (x − 1)), x⟶1−0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
2
1
−∞
Найти предел lim (√(1 + x) − 1) / sin3x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
1/6
2
Найти предел lim (1 + 5 / x)²ˣ, x⟶∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
eˣ
e¹⁰
Найти предел lim (1 + x)^(2/x), x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
e²
e⁻²
Найти предел lim (1 − cos5x) / x², x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2.5
12.5
Найти предел lim (2x² / (3 + x²) + 5^(1 / x)), x⟶∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
5
5/3
3/5
Найти предел lim (3n − 2) / ∛(n³− 5n² + 1), n⟶∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
2
3
1
Найти предел lim (3x² + 4x - 3) / (6x² + 5x + 7), x⟶+∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
1/2
2
5
Найти предел lim (3x³ + 4x² + 5) / (x⁴ − 3x + 2), x⟶+∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
3
1
2
Найти предел lim (4x - 7) / (5 - 2x), x⟶+∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
-2
-1
2
Найти предел lim (4x² - x + 7) / (3x + 1), x⟶2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1;
2
3
Найти предел lim (eªˣ − eᵇˣ) / sinx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
а + b
∞
−∞
а – b
1
Найти предел lim (eˣ − 1) / (√(1 + x) − 1), x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2
3
Найти предел lim (x − 5) / (2 − √(x − 1)), x⟶5
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
4
-4
1/2
Найти предел lim (x² - 9) / (√(x + 1) - 2), x⟶3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
24
18
Найти предел lim (x⁴ - 1) / (x³ - 1), x⟶1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
3/4
4/3
2
Найти предел lim arctgx / x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
3
2
1
Найти предел lim ln(1 + x) / arcsinx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
1/2
2
Найти предел lim sin10x / x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
10
∞
5
Найти предел lim sin2x / arcsin3x, x⟶0 @
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2/3
3
Найти предел lim sin²x / x², x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2
10
Найти предел lim tg³x / x³, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
3
2
Найти предел lim tg5x / x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
5
3
Найти предел lim x / arctgx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
3
1
2
Найти предел, пользуясь правилом Лопиталя: lim (eˣ − 1) / (sin2x), x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
-∞
2
0.5
Найти предел, пользуясь правилом Лопиталя: lim x / lnx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
-∞
1
0
-1
Найти предел: lim (1 − tgx) / cos2x, x⟶π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
-1
1
∞
5
Найти предел: lim lnx / (1 − x²), x⟶1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3
2
−1/3
1/3
∞
Найти производную y'ₓ от функции, заданной параметрически {x = atcost; y = atsint, где t ∈ [0; 2π]
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(asint + tcost) / (acost + tsint)
(sint - tcostt) / (cost + tsintt)
(sint + atcost) / (cost − atcost)
(sint + tcostt) / (cost − tsintt)
(sint + tcost) / (cost − tsint)²
Найти производную y'ₓ от функции, заданной параметрически {x = t², y = 4tпри t = 1, где t∈ [−∞; +∞]
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
1,1
2,2
Найти третий дифференциал функции y = 3x² - 5x + 2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3dx³
6xdx³
2dx³
0
dx³
Наклонной асимптотой графика функции y = x³ / (x² − 3) является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = 0
у = 3х
у = х
у =2х
∅
Нормаль к графику функции y = eˣ в точке M₀(0; 1) определяется уравнением
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = х + 1
у = 2х – 1
у = 2х
у = –х + 1
у = х – 1
Нормаль к графику функции y = x² в точке M₀(1; 1) определяется уравнением
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = х + 2
у = х – 2
y = −1/2 ⋅ x − 3/2
y = −1/2 ⋅ x + 3/2
y = 1/2 ⋅ x − 3/2
Областью определения функции у = arc sin x является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x ∈ (−∞; +∞);
x ∈ [0; +∞);
x ∈ [−1; 1];
x ∈ (−1; 1);
x ∈ [0; 1].
Областью определения функции y = (5 − x) / √(x² − 8x + 7) является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x ∈ (−∞; +∞);
x ∈ (1; 7);
x ∈ [1; 7);
x ∈ (−∞; 1) ⋃ (7; +∞);
x ∈ (−∞; 1] ⋃ [7; +∞).
Последовательность {−1/n} имеет своим пределом
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
1
2
10
Производная (x / 3)' равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x² / 9
1/3
−x / 9
x / 3
−1/3
Производная (x² / 2)' равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2х
х
−x² / 4
x / 2
Производная функции у = arcsin3x равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 / √(1 − x²)
3 / √(1 − 9x²)
1 / √(1 − 9x²)
3x / √(1 − 9x²)
x / √(1 − 9x²)
Производная функции у = sin 2x при x = π/2 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
-1
-2
2
Производная функции у = tg 3x равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3 sec² 3x
−3 sec² 3x
3 tg * secx
−3 tg * secx
3 ctg 3x
Производная функции у(х) = с равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
с
1
0
х
сх
Производная функции у(х) = х равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
х
x²
1
2х
Производная функции eʸ + x = y равна:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x / (1 + eʸ)
x / (1 − eʸ)
1 / (1 − eʸ)
y / (1 + eʸ)
xy / (1 + eʸ)
Производная функции y = 3x² − 5x + 2 при х = 1 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
-1
6
5
Производная функции y = 5³ˣ равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
5³ˣ
3x ⋅ 5³ˣ⁻¹
3 ⋅ 5³ˣln5
5³ˣln5
3 ⋅ 5³ˣ
Производная функции y = eˣ / (x + 1) равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
eˣ
−eˣ / (x + 1)²
−e / (x + 1)²
+eˣ / (x + 1)²
xeˣ / (x + 1)²
Производная функции y = log₅(3x² − 5) равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 / (3x² − 5)
1 / (3x² − 5)ln5
3x² − 5
6x / (3x² − 5)ln5
6x / (3x² − 5)
Производная функции y = sin 3x равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
–3cos 3x
cos 3x
3sin 3x
3cos 3x
–3sin 3x
Производная функции y = x / (eˣ + 1) при х = 0 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
1/2
3
-1
Производная функции y = xeˣ при х = 0 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2
3
1
0
-1
Разложить число 10 на два слагаемых, так чтобы произведение было их наибольшим.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3; 7
6; 4
1; 9
5; 5
2; 8
Решеткой длиной 120 м нужно огородить прилегающую к дому площадку наибольшей площади. Определить размеры прямоугольной площадки.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
20 м; 80 м
40 м; 40 м
30 м; 60 м
25 м; 70 м
35 м; 50 м
Сколько однозначных функций задано уравнением y² = x
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
3
4
Сравнить бесконечно малую α и β = α³ Бесконечно малая β по сравнению с бесконечно малой α является :
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
одного порядка;
второго порядка;
третьего порядка;
бесконечно большой;
эквивалентной.
Стационарными точками функции x³ / 3 - 11 / 2 ⋅ x² + 30x + 2 являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2,3
5,6
1,3
0,2
4,8
Стационарными точками функции y = e^(x² - 2x) являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2
3
4
1
-1
Стационарными точками функции y = x³ / 3 - 3x² + 5x - 2 являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,1
1,5
2,3
1,2
3,4
Точками разрыва заданной функции y = (2x - 1) / (x² - 8x + 15) являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2
1, 2
2, 4
3, 5
0, 2
Точками разрыва заданной функции y = x / 4 + 4 / x являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2, 3
4
5
0
Точками разрыва функции y = 2^(1/x) являются
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
1
−∞
0
2
Точками разрыва функции y = 3 / (√(x + 2) - 2) являются
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
4
7
Точками разрыва функции y = 5 / (sinx − 1/2) являются
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2πk;
πk;
(−1)ᵏ ⋅ π/6 + πk;
π/2 + πk;
(−1)ᵏ ⋅ π/4 + πk.
Функция y = (x - 1) / (x² - 5x + 7) является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из
нескольких предложенных вариантов
трансцендентной,
иррациональной,
целое рациональное,
правильная рациональная дробь,
неправильная рациональная дробь.
Функция y = 4x⁵ - 3x + 2 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
трансцендентной,
иррациональной,
целое рациональное,
правильная рациональная дробь,
неправильная рациональная дробь.
Функция y = 7x² - 5√x - 2 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
трансцендентной,
иррациональной,
целое рациональное,
правильная рациональная дробь,
неправильная рациональная дробь.
Частным значение функции y = x² + 2 при х = 3 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
-1
11
0
-3
-5
Частным значением функции y = {x при x ≤ 0; x² + 3 при x > 0 при х = 3 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2
5
12
0
4Показать/скрыть дополнительное описание
Тема 1. Функция. Способы задания. Неявная функция. Обратная функция. Классификация функций
Тема 2. Теория пределов
Тема 3. Предел функции. Непрерывность функции. Разрыв функции. Основные свойства непрерывных функций
Тема 4. Замечательные пределы. Сравнение бесконечно малых величин. Эквивалентные бесконечно малые величины
Тема 5. Дифференцирование функций. Часть 1
Тема 6. Дифференцирование функций. Часть 2
Тема 7. Дифференциал функции. Производные и дифференциалы высших порядков
Тема 8. Аналитические приложения дифференцируемых функций
Тема 9. Экстремум функции
Тема 10. Неопределенный интеграл. Основные свойства. Таблица неопределенных интегралов. Метод непосредственного интегрирования
Тема 11. Неопределенный интеграл. Основные методы интегрирования
Тема 12. Определенный интеграл. Определенный интеграл. Задачи, приводящие к понятию определенного интеграла
Тема 13. Приложения определенного интеграла
Тема 14. Основы линейной алгебры. Матрицы. Виды матриц. Операции над матрицами
Тема 15. Теория определителей. Основные свойства определителей. Вычисление определителей произвольного порядка n. Формулы разложения
Тема 16. Обратная матрица. Ранг матрицы. Понятие обратной матрицы
Тема 17. Системы линейных алгебраических уравнений
Абсциссами точек перегиба графика функции y = x³ / 6 − x² / 2 являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
3
4
Абсциссами точек перегиба графика функции y = x³ являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2
3
0
4
Боковые стороны и меньшее основание трапеции равны по 10 см. Определить ее большее основание так, чтобы площадь трапеции была наибольшей.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
13 см
15 см
22 см
20 см
25 см
Вертикальными асимптотами графика функции y = lnx являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
х = е
х = 0
х = 1
х = –1
∅
Выберите правильный ответ на вопрос: производная [c ⋅ u(x) - d ⋅ v(x)]'], гдеси d —действительныечисла, равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
c' ⋅ u(x) − d' ⋅ v(x)
c ⋅ u'(x) + d ⋅ v'(x)
c ⋅ u'(x) − d ⋅ v'(x)
c ⋅ u'(x) − d ⋅ v(x)
0
Выберите правильный ответ на вопрос: производная [u(x) ⋅ v(x)]' равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
u'(x) ⋅ v(x)
u(x) ⋅ v'(x)
u'(x) ⋅ v'(x)
u'(x) + v'(x)
u'(x)v(x) + u(x)v'(x)
Выберите правильный ответ на вопрос. Производная функции [u(x) / c]', где с — действительное число, равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
u'(x) / c'
cu'(x)
−u'(x) / c
u'(x) / c
u'(x) / c²
Вычислить ∫ √(4 − 5x)dx, x=−12..−1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
54 2/3
18 1/3
64 2/3
15
10
Вычислить ∫ dx / (a² + x²), x=a..a√3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
π / 2a
π / 3a
π / 12a
π / 4a
π / 6a
Вычислить ∫ dx / (x² + 6x + 8), x=2..8
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2 ⋅ ln(5/4)
ln(5/4)
3/4 ⋅ ln(5/4)
3 ⋅ ln(5/4)
2ln3
Вычислить ∫ dx / √(x² + 1), x=0..1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 + √2
ln2 + 1
2 ⋅ ln│1 + √2│
3 ⋅ ln│1 + √2│
ln│1 + √2│
Вычислить ∫ e^(x/3)dx, x=0..3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
е –1
2(e + 1)
2(e - 1)
3(e - 1)
1/2 ⋅ (e - 1)
Вычислить ∫ sin2xdx, x=0..π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
0
2
3/2
1/2
Вычислить ∫ sin4xdx, x=0..π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
1/3
2
1/2
Вычислить ∫ x³dx, x=1..3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
10
15
-20
-10
20
Вычислить ∫ xe^(x²)dx, x=0..1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
е –1
2е –1
3е +1
(e + 1) / 2
(e − 1) / 2
Вычислить ∫ xeˣdx, x=0..1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
2
1
3
4
Вычислить приближенно приращение функции y = x² + 2x + 3 когда х изменяется от 2 до 1,98.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,3
–0,5
0,01
–0,12
0,05
Геометрически первая производная от функции, если она существует, есть
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Синус угла наклона касательной к оси ОХ
Косинус угла наклона касательной к оси ОХ
Тангенс угла наклона касательной к оси ОХ
Котангенс угла наклона касательной к оси ОХ
Дифференциал функции y = sin²2x равен
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2 sin 2 xdx
2 cos2 xdx
–2 sin 2 xdx
sin 4 xdx
2 sin 4 xdx
Дифференциал функции y = x³ + 3x² + 3x равен
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(6x⁴ + 3x³ + 3x³)dx
(3x² + 6x + 3)dx
(3x² + 6x)dx
(x⁴ / 4 + x³ + 3 ⋅ x² / 2)dx
(x⁴ + 3x + 3)dx
Достаточными условиями существования производной непрерывной функции в точке являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Существование хотя бы одной односторонней производной
Существование двух односторонних производных
Существование и равенство двух односторонних производных
Заменив приращение функции дифференциалом, приближенно найти arctg 1,05.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,75
0,69
0,81
0,80
0,65
Заменив приращение функции дифференциалом, приближенно найти sin 31°.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,500
0,451
0,35
0,515
0,491
Из непрерывности функции
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
следует ее дифференцируемость
еще не следует ее дифференцируемость
следует разрывность первой производной
следует непрерывность первой производной
Какая из заданных функций задана явно:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
ху = 5;
x² + y² = 9;
у = sinx;
eˣʸ = 3;
lg(x + y) = 5.
Какая из заданных функций является обратной для функции Y=5x-3:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x = (y − 3) / 5;
x = (y + 3) / 5;
x = (5y − 3) / 5;
x = (3y − 5) / 5;
x = (3y + 5) / 5.
Какая из заданных функций является четной:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
y = x² - x;
y = x⁴ - 2x²;
y = x⁴ - x²;
y = x + 2;
y = x.
Касательная к графику функции y = x² в точке M₀(1; 1) определяется уравнением
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = х + 1
у = 2х – 1
у = 2х + 1
у = х –1
у = 2х + 3
Наибольшим значением функции y = x² − 2x на отрезке [–1; 1] является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
-1
3
5
∞
10
Найдите вторую производную заданной функции y = x / (x − 1)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
−1 / (x − 1)²
−1 / (x − 1)³
1 / (x − 1)⁴
2 / (x − 1)³
−2 / (x − 1)³
Найдите вторую производную функции у = sin2x.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2 sin 2x
4 cos 2x
– 4sin 2x
4 sin 2x
cos 2x
Найти все точки разрыва функции y = (2x - 1) / (x² - 8x + 15)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2
2 и 6
1 и 2
3 и 5
1 и 4
Найти интеграл ∫ ((√x - 1)² / x)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x√x − 2√x + ln|x| + c
x − 4√x + ln|x| + c
√x − 4x + ln|x| + c
√x − 2√x + ln|x| + c
x + 2√x + ln|x| + c
Найти интеграл ∫ ((10x⁵ + 5) / x³ )dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
10x³ + x² + c
10x² + x + c
10 / 3 ⋅ x³ - 5 / (2x²) + c
10 / 3 ⋅ x² - 5 / (2x) + c
10 / 3 ⋅ x - 5 / (2x) + c
Найти интеграл ∫ (√x + ∛x)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x√x + x∛x + c
2/3 ⋅ x√x − 3/4 ⋅ x∛x + c
2 ⋅ x√x + 3 ⋅ x∛x + c
3/2 ⋅ x√x + 4/3 ⋅ x∛x + c
2/3 ⋅ x√x + 3/4 ⋅ x∛x + c
Найти интеграл ∫ (2 / (1 + x²) − 3 / √(1 − x²))dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2 ⋅ arctgx − 3 ⋅ arcsinx + c
1/2 ⋅ arctgx + arcsinx + c
2 ⋅ arctgx − arccosx + c
2 ⋅ arcsinx − 3 ⋅ arctgx + c
2 ⋅ arccosx + 3 ⋅ arctgx + c
Найти интеграл ∫ (4 − 3x)e⁻²ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x / 4 ⋅ e⁻²ˣ + C
(2x − 3) / 4 ⋅ e⁻²ˣ + C
3xe⁻²ˣ + C
(5 − 6x) / 4 ⋅ e⁻²ˣ + C
(6x − 5) / 4 ⋅ e⁻²ˣ + C
Найти интеграл ∫ ⁵√(x³)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/5 ⋅ x ⋅ ⁵√(x³) + c
5/8 ⋅ x ⋅ ⁵√(x³) + c
3/5 ⋅ x^(3/5) + c
−5/2 ⋅ x^(−2/5) + c
5/8 ⋅ x² ⋅ ⁵√(x³) + c
Найти интеграл ∫ aˣ(1 + a⁻ˣ / √(x³))dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из
нескольких предложенных вариантов
aˣ / lna − 3/2 ⋅ √x + c
aˣ / lna + 3/2 ⋅ √x + c
aˣ / lna − 3/2 ⋅ ∛x + c
aˣ / lna − 2/2 ⋅ ∛x + c
aˣ / lna + 3/2 ⋅ ∛x + c
Найти интеграл ∫ cos2xdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
-1/2 ⋅ sin2x + C
1/2 ⋅ sinx + C
cos²2x / 2 + C
1/2 ⋅ sin2x + C
sin2x + C
Найти интеграл ∫ dx / (√x + 1)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
ln│√x + 1│+ C
1/2 ⋅ ln│√x + 1│+ C
√x + 2ln│√x + 1│+ C
2√x − 2ln│√x + 1│+ C
2√x + 2ln│√x + 1│+ C
Найти интеграл ∫ cos²xdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
cos³x / 3 + c
1/2 ⋅ x + 1/4 ⋅ sin2x + c
1/2 ⋅ cos³x + c
x + sin2x + c
1/2 ⋅ x - 1/4 ⋅ sin2x + c
Найти интеграл ∫ dx / (x² + 6x + 13)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
arcsin(x + 3) + c
arcsin((x + 3) / 2) + c
arctg(x + 3) + c
1/2 ⋅ arctg((x + 3) / 2) + c
2arctg(x + 3) + c
Найти интеграл ∫ dx / √(4 − x²)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
arcsinx + c
arccosx + c
arcsin(x/2) + c
arctg(x/2) + c
1/2 ⋅ arctg(x/2) + c
Найти интеграл ∫ dx / √(x² + 3x)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2 ⋅ √(x² + 3x) + C
ln│x + 3/2 + √(x² + 3x)│+ C
2 ⋅ √(x² + 3x) + C
3 ⋅ ln│x + √(x² + 3x)│
ln│x + √(x² + 3x)│
Найти интеграл ∫ e⁵⁻³ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(5 - 3x)e⁵⁻³ˣ + C
−1/3 ⋅ e⁵⁻³ˣ + C
e⁵⁻³ˣ + C
1/3 ⋅ e⁵⁻³ˣ + C
e⁵⁻³ˣ ⋅ ln|5 − 3x| + C
Найти интеграл ∫ eˣdx / (e²ˣ − a²)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 / (2a) ⋅ ln│(eˣ − a) / (eˣ + a)│+ C
e²ˣ − a² + C
1 / a ⋅ (e²ˣ − a²)│+ C
1 / a ⋅ ln│e²ˣ − a²│+ C
1 / (2a) ⋅ ln│e²ˣ − a²│+ C
Найтиинтеграл ∫ x√(3 − 5x)dx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(5x + 2)√(3 - 5x) + C
(5x - 3)√(3 - 5x) + C
2/125 ⋅ (5x + 2)(5x - 3)√(3 - 5x) + C
(5x + 2)(5x - 3)√(3 - 5x) + C
(5x + 2)(5x + 3)√(3 - 5x) + C
Найти интеграл ∫ x²e⁻ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(x² + 2x + 2)e⁻ˣ + C
−(x² + 2x + 2)e⁻ˣ + C
(x² + 2)e⁻ˣ + C
(x² + 2x)e⁻ˣ + C
(x² − 2x + 2)e⁻ˣ + C
Найти интеграл ∫ x³dx / (x⁴ + 5)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
ln(x⁴ + 5) + c
4 ⋅ ln(x⁴ + 5) + c
1/4 ⋅ ln(x⁴ + 5) + c
−ln(x⁴ + 5) + c
−1/4 ⋅ ln(x⁴ + 5) + c
Найти интеграл ∫ xe⁻²ˣdx
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x / 4 ⋅ e⁻²ˣ + C
−(2x +1) / 4 ⋅ e⁻²ˣ + C
(x +1) / 2 ⋅ e⁻²ˣ + C
(2x +1) / 4 ⋅ e⁻²ˣ + C
− x / 4 ⋅ e⁻²ˣ + C
Найти интервалы монотонного возрастания функции y = 6x² - 3x.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(−∞; 1/4);
(0; 1/4);
(−∞; 3)
(1/4; +∞);
(2; +∞).
Найти интервалы монотонного убывания функции y = x³ − 3x²
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(–2; 2);
(1; 2);
(–1; 1);
(0; 2);
(0; 3).
Найти объём тела, полученного от вращения плоской фигуры, ограниченной линиями y = sinx; x = π/2, y = 0 вокруг оси Ох.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из
нескольких предложенных вариантов
π² (куб. ед.);
π 2/4 (куб. ед.);
π (куб. ед.);
3/4 π² (куб. ед.);
2π (куб. ед.).
Найти площадь плоской фигуры, ограниченной линиями у = sinx, у = cosx, x = 0; x = π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
√2 (кв.ед.);
√2/2 (кв.ед.);
(√2 − 1) (кв.ед.);
3 (кв.ед.);
2 (кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями x = y² и у = –х + 2.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
4,5 (кв.ед.);
2,5 (кв.ед.);
3 (кв.ед.);
2 (кв.ед.);
3,5 (кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями y = √(lnx), y = 0, x = e вокруг оси Ох.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2π (куб. ед.);
3π (куб. ед.);
π (куб. ед.);
4π (куб. ед.);
5π (куб. ед.).
Найти площадь плоской фигуры, ограниченной линиями y = lnx, y = 0, x = e вокруг оси Ох.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2
3
e
5
Найти площадь плоской фигуры, ограниченной линиями y = x² - 2x + 1 у = 1.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3
4/3 (кв.ед.);
1/3 (кв.ед.);
5 (кв.ед.);
5/3 (кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями y = x² - 4x + 5; y = 5.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
8 2/3
10 2/3 (кв.ед.);
7 1/3 (кв.ед.);
10;
7 2/3(кв.ед.).
Найти площадь плоской фигуры, ограниченной линиями y = x² - 9, у = 0.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
–36 кв.ед.;
18 кв.ед.;
54 кв.ед.;
36 кв.ед.;
26 кв.ед.
Найти предел на основании свойств пределов lim (4x³ − 2x² + 5x − 1), x⟶2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
26
33
18
Найти предел функции lim (3x² - 5x + 2), x⟶2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
2
4
22
1
Найти предел функции lim 2^(1 / (x − 1)), x⟶1−0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
2
1
−∞
Найти предел lim (√(1 + x) − 1) / sin3x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
1/6
2
Найти предел lim (1 + 5 / x)²ˣ, x⟶∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
eˣ
e¹⁰
Найти предел lim (1 + x)^(2/x), x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
e²
e⁻²
Найти предел lim (1 − cos5x) / x², x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2.5
12.5
Найти предел lim (2x² / (3 + x²) + 5^(1 / x)), x⟶∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
5
5/3
3/5
Найти предел lim (3n − 2) / ∛(n³− 5n² + 1), n⟶∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
2
3
1
Найти предел lim (3x² + 4x - 3) / (6x² + 5x + 7), x⟶+∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
1/2
2
5
Найти предел lim (3x³ + 4x² + 5) / (x⁴ − 3x + 2), x⟶+∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
3
1
2
Найти предел lim (4x - 7) / (5 - 2x), x⟶+∞
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
-2
-1
2
Найти предел lim (4x² - x + 7) / (3x + 1), x⟶2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1;
2
3
Найти предел lim (eªˣ − eᵇˣ) / sinx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
а + b
∞
−∞
а – b
1
Найти предел lim (eˣ − 1) / (√(1 + x) − 1), x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2
3
Найти предел lim (x − 5) / (2 − √(x − 1)), x⟶5
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
4
-4
1/2
Найти предел lim (x² - 9) / (√(x + 1) - 2), x⟶3
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
24
18
Найти предел lim (x⁴ - 1) / (x³ - 1), x⟶1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
3/4
4/3
2
Найти предел lim arctgx / x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
3
2
1
Найти предел lim ln(1 + x) / arcsinx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
1/2
2
Найти предел lim sin10x / x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
10
∞
5
Найти предел lim sin2x / arcsin3x, x⟶0 @
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2/3
3
Найти предел lim sin²x / x², x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
2
10
Найти предел lim tg³x / x³, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
3
2
Найти предел lim tg5x / x, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
1
5
3
Найти предел lim x / arctgx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
3
1
2
Найти предел, пользуясь правилом Лопиталя: lim (eˣ − 1) / (sin2x), x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
∞
-∞
2
0.5
Найти предел, пользуясь правилом Лопиталя: lim x / lnx, x⟶0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
-∞
1
0
-1
Найти предел: lim (1 − tgx) / cos2x, x⟶π/4
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
-1
1
∞
5
Найти предел: lim lnx / (1 − x²), x⟶1
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3
2
−1/3
1/3
∞
Найти производную y'ₓ от функции, заданной параметрически {x = atcost; y = atsint, где t ∈ [0; 2π]
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
(asint + tcost) / (acost + tsint)
(sint - tcostt) / (cost + tsintt)
(sint + atcost) / (cost − atcost)
(sint + tcostt) / (cost − tsintt)
(sint + tcost) / (cost − tsint)²
Найти производную y'ₓ от функции, заданной параметрически {x = t², y = 4tпри t = 1, где t∈ [−∞; +∞]
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
1,1
2,2
Найти третий дифференциал функции y = 3x² - 5x + 2
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3dx³
6xdx³
2dx³
0
dx³
Наклонной асимптотой графика функции y = x³ / (x² − 3) является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = 0
у = 3х
у = х
у =2х
∅
Нормаль к графику функции y = eˣ в точке M₀(0; 1) определяется уравнением
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = х + 1
у = 2х – 1
у = 2х
у = –х + 1
у = х – 1
Нормаль к графику функции y = x² в точке M₀(1; 1) определяется уравнением
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
у = х + 2
у = х – 2
y = −1/2 ⋅ x − 3/2
y = −1/2 ⋅ x + 3/2
y = 1/2 ⋅ x − 3/2
Областью определения функции у = arc sin x является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x ∈ (−∞; +∞);
x ∈ [0; +∞);
x ∈ [−1; 1];
x ∈ (−1; 1);
x ∈ [0; 1].
Областью определения функции y = (5 − x) / √(x² − 8x + 7) является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x ∈ (−∞; +∞);
x ∈ (1; 7);
x ∈ [1; 7);
x ∈ (−∞; 1) ⋃ (7; +∞);
x ∈ (−∞; 1] ⋃ [7; +∞).
Последовательность {−1/n} имеет своим пределом
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
0
1
2
10
Производная (x / 3)' равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x² / 9
1/3
−x / 9
x / 3
−1/3
Производная (x² / 2)' равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2х
х
−x² / 4
x / 2
Производная функции у = arcsin3x равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 / √(1 − x²)
3 / √(1 − 9x²)
1 / √(1 − 9x²)
3x / √(1 − 9x²)
x / √(1 − 9x²)
Производная функции у = sin 2x при x = π/2 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
-1
-2
2
Производная функции у = tg 3x равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3 sec² 3x
−3 sec² 3x
3 tg * secx
−3 tg * secx
3 ctg 3x
Производная функции у(х) = с равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
с
1
0
х
сх
Производная функции у(х) = х равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
х
x²
1
2х
Производная функции eʸ + x = y равна:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
x / (1 + eʸ)
x / (1 − eʸ)
1 / (1 − eʸ)
y / (1 + eʸ)
xy / (1 + eʸ)
Производная функции y = 3x² − 5x + 2 при х = 1 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
-1
6
5
Производная функции y = 5³ˣ равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
5³ˣ
3x ⋅ 5³ˣ⁻¹
3 ⋅ 5³ˣln5
5³ˣln5
3 ⋅ 5³ˣ
Производная функции y = eˣ / (x + 1) равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
eˣ
−eˣ / (x + 1)²
−e / (x + 1)²
+eˣ / (x + 1)²
xeˣ / (x + 1)²
Производная функции y = log₅(3x² − 5) равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1 / (3x² − 5)
1 / (3x² − 5)ln5
3x² − 5
6x / (3x² − 5)ln5
6x / (3x² − 5)
Производная функции y = sin 3x равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
–3cos 3x
cos 3x
3sin 3x
3cos 3x
–3sin 3x
Производная функции y = x / (eˣ + 1) при х = 0 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
1/2
3
-1
Производная функции y = xeˣ при х = 0 равна
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2
3
1
0
-1
Разложить число 10 на два слагаемых, так чтобы произведение было их наибольшим.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
3; 7
6; 4
1; 9
5; 5
2; 8
Решеткой длиной 120 м нужно огородить прилегающую к дому площадку наибольшей площади. Определить размеры прямоугольной площадки.
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
20 м; 80 м
40 м; 40 м
30 м; 60 м
25 м; 70 м
35 м; 50 м
Сколько однозначных функций задано уравнением y² = x
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
3
4
Сравнить бесконечно малую α и β = α³ Бесконечно малая β по сравнению с бесконечно малой α является :
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
одного порядка;
второго порядка;
третьего порядка;
бесконечно большой;
эквивалентной.
Стационарными точками функции x³ / 3 - 11 / 2 ⋅ x² + 30x + 2 являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2,3
5,6
1,3
0,2
4,8
Стационарными точками функции y = e^(x² - 2x) являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2
3
4
1
-1
Стационарными точками функции y = x³ / 3 - 3x² + 5x - 2 являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0,1
1,5
2,3
1,2
3,4
Точками разрыва заданной функции y = (2x - 1) / (x² - 8x + 15) являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1/2
1, 2
2, 4
3, 5
0, 2
Точками разрыва заданной функции y = x / 4 + 4 / x являются:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
1
2, 3
4
5
0
Точками разрыва функции y = 2^(1/x) являются
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
∞
1
−∞
0
2
Точками разрыва функции y = 3 / (√(x + 2) - 2) являются
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
0
1
2
4
7
Точками разрыва функции y = 5 / (sinx − 1/2) являются
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2πk;
πk;
(−1)ᵏ ⋅ π/6 + πk;
π/2 + πk;
(−1)ᵏ ⋅ π/4 + πk.
Функция y = (x - 1) / (x² - 5x + 7) является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из
нескольких предложенных вариантов
трансцендентной,
иррациональной,
целое рациональное,
правильная рациональная дробь,
неправильная рациональная дробь.
Функция y = 4x⁵ - 3x + 2 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
трансцендентной,
иррациональной,
целое рациональное,
правильная рациональная дробь,
неправильная рациональная дробь.
Функция y = 7x² - 5√x - 2 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
трансцендентной,
иррациональной,
целое рациональное,
правильная рациональная дробь,
неправильная рациональная дробь.
Частным значение функции y = x² + 2 при х = 3 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
-1
11
0
-3
-5
Частным значением функции y = {x при x ≤ 0; x² + 3 при x > 0 при х = 3 является:
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
2
5
12
0
4Показать/скрыть дополнительное описание
Высшая математика Темы 1-17.
Список вопросов
Даны прямые (x + 2) / 2 = y / -3 = (z - 1) / 4 и (x - 3) / α = (y - 1) / 4 = (z - 7) / 2. При каком значении α они перпендикулярны?
Найдите острый угол между прямыми (x - 1) / 1 = (y + 2) / -1 = z / √2 и (x + 2) / 1 = (y - 3) / 1 = (z + 5) / √2
Укажите уравнение окружности, которая проходит через точку А(3;1), а ее центр лежит на прямой 3x - y - 2 = 0
Укажите канонические уравнения прямой {x + 3y - 5z - 7 = 0; 2x - 3y + 3z + 4 = 0
Какой из перечисленных векторов коллинеарен вектору AB = (4; -8)?
Найдите общее решение системы {9x₁ − 3x₂ + 5x₃ + 6x₄ = 4; 6x₁ − 2x₂ + 3x₃ + 4x₄ = 5; 3x₁ − x₂ + 3x₃ + 14x₄ = −8
С помощью метода Крамера (определителей) можно найти решение …
Напишите каноническое уравнение гиперболы, фокусы которой лежат на оси Ox, если даны a = 6 и b = 2
Найдите АВ - АС, где A = ((2, -3), (0, 1)); B = ((1, 3), (0, 4))
Укажите натуральный ряд чисел
При каком положительном значении параметра t прямые, заданные уравнениями 3tx - 8y +1 = 0 и (1 + t)x - 2ty = 0, параллельны?
Вычислите выражение ((13 1/4 - 2 5/27 - 10 5/6) ⋅ 230,04 + 46,75) / 0,01
Найдите значение выражения -3 ⋅ (2/3)² - 0,5²
Упростите выражение 5 / (1 + 4 / x) ⋅ ((x − 4) / (x² + 4x) − 16 / (16 − x²))
Определитель системы трех линейных неоднородных уравнений с тремя неизвестными равен 5. Это означает, что …
Установите взаимное расположение прямых (x - 2) / 4 = (y + 1) / -3 = (z - 1) / -2 и (x - 7) / 5 = (y - 1) / 6 = (z - 3) / 1
Даны вершины треугольника ABC: A(3; -1), B(4; 2) и C(-2; 0). Укажите уравнения его сторон
Раскройте определитель │(a, b), (b, a)│
Укажите уравнение окружности, проходящей через точку (4; 5), с центром в точке (1; -3)
Найдите А · В, где A = ((5, 0, 2, 3), (4, 1, 5, 3), (3, 1, -1, 2)); B = ((6), (-2), (7), (4))
Вычислите определитель │(5, -1), (2, 4)│
Вычислите с точностью до десятых (3/5 + 0,425 - 0,005) : 0,1 / (30,5 + 1/3 + 3 1/3)
Уравнение 3x - 4y + 12 = 0 преобразуйте к уравнению в отрезках
Вычислите определитель │(1, 3, -2), (5, 1, 4), 3, 2, 1)│
Укажите уравнение окружности радиуса R = 8 с центром в точке C(2; -5)
Матрица А^-1 является обратной матрицей к матрице А, если
Какое из перечисленных чисел является иррациональным?
Вычислите произведение матриц ((1, 2), (−2, −1)) ⋅ ((3, 0), (−2, 1))
Даны точки M (-5; 7; -6), N (7; -9; 9). Вычислите проекцию вектора a = {1; -3; 1} на вектор MN
Вычислите определитель D =│(1, -2, 3), (3, 5, -1), (4, 1, 2)│
Найдите обратную матрицу для матрицы A = ((2, 2, 3), (1, −1, 0), (−1, 2, 1))
Метод Гаусса решения системы линейных уравнений предполагает использование …
Найдите промежутки возрастания или убывания функции y = - 2x^2 + 8x - 1
Вычислите определитель матрицы системы {2x - 4y = 1; 3x + 5y = -2
Каково необходимое условие возрастания функции?
Найдите общее решение уравнения xy^2dy = (x^3 + y^3)dx
Найти решение системы {2x - 4y + 3z = 1; x - 2y + 4z = 3; 3x - y + 5z = 2
Найдите общее решение уравнения y'' - 9y = e²ˣ
Укажите уравнение окружности, которая проходит через точку А(2; 6) и центр которой совпадает с точкой C(-1; 2)
Найдите координаты точки пересечения прямых 2x - y - 3 = 0 и 4x + 3y - 11 = 0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Упростите иррациональное выражение √((-22)²)
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Дано: |a₁| = 3, |a₂| = 4, (a₁, a₂) = 2π/3. Вычислите (a₁ + a₂)²
Найдите общее решение уравнения x² ⋅ d²y / dx² = 2
Напишите каноническое уравнение эллипса, если даны его полуоси a = 5 и b = 4
Система линейных уравнений называется совместной, если она …
Решите матричное уравнение AX + AXA = B, где A = ((1, 2), (0, 3)); B = ((4, 8), (6, 6))
Матричное уравнение А⸱Х =В имеет решение …
Матрица называется невырожденной, если ее определитель …
Скалярным произведением двух векторов называется …
Векторы AC = a и BD = b служат диагоналями параллелограмма ABCD. Выразите вектор DA через векторы a и b
Найдите координаты точки K пересечения прямой (x - 1) / 2 = (y - 2) / 3 = (z - 3) / 4 с плоскостью 2x + 5y - 3z = 0
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Тип ответа: Одиночный выбор • с выбором одного правильного ответа из нескольких предложенных вариантов
Найдите ∫ 3dt / 2t
Среди перечисленных дифференциальных уравнений укажите однородное уравнение
Найдите предел lim tg5x / x, x⟶0
Система линейных уравнений называется определенной, если она …
Найдите предел lim (2x + 1) / (x² - 3), x⟶∞
Вычислите (3 12/17 + 4 5/21) - 1 12/17
Укажите уравнение окружности, центр которой совпадает с началом координат, а прямая 3x - 4y + 20 = 0 является касательной к окружности
Определите уравнение прямой, отсекающей на оси Oy отрезок b = 2 и составляющей с осью Ox угол = 45°
Найдите ∫ dx / cos²(1 - 2x)
![]()
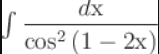
Найдите точки максимума (минимума) функции y= -5x^2- 2x + 2
Для функции y = sinx / x
Вычислите определенный интеграл ∫ √(x)dx, x = 1..4
Найдите общее решение уравнения y'' - y = 0
При каком значении l векторы MP и KD коллинеарны, если M(-3; 2), P(-1; -2), K(2; 1), D(5; l)?
Найдите предел lim (5ˣ - cosx), x⟶0
Найдите предел lim (√(1 + 6x) - 5) / (√x - 2), x⟶4
Определите полуоси гиперболы x² / 16 - y² = 1
Составьте уравнение плоскости, зная, что точка А(1, -1,3) служит основанием перпендикуляра, проведенного из начала координат к этой плоскости.
Найдите производную функции y = xe^x - e^x
Вычислите определенный интеграл ∫ dx / (1 - 2x)³, x = -2..0
Дано: │a│= 8,│b│= 8, (a, b) = π/3. Найдите a ⋅ b.
Найдите уравнение прямой, проходящей через точку пересечения прямых 2x + 3y - 8 = 0 и x - 4y + 5 = 0 и через точку M1(-2; 3)
Найдите предел lim tg3x / sin5x, x⟶0
Найдите предел lim (1 - 5 / x)ˣ, x⟶∞
Найдите ∫ (x - 3)dx, если при x= 2 первообразная функция равна
Вертикальные асимптоты к графику функции y = (x + 2) / (x² - 4x)
Найдите точки перегиба кривой y = x^4 - 12x^3 + 48x^2 - 50
Среди перечисленных дифференциальных уравнений укажите уравнение Бернулли
Уравнение y + xy’ -2 = 0 является …
Число f(x0) называется наибольшим значением функции на отрезке [a;b], если …
Найдите уравнение прямой, проходящей через точки M1(3; 2), M2(4; -1)
Найдите предел lim 2x / (x - 1), x⟶0
Найдите общее решение уравнения y'' - 4y' + 3y = 0
Найдите ∫ 2xdx
Укажите каноническое уравнение эллипса, расстояние между фокусами которого равно 8, а малая полуось b = 3
Уравнение, связывающее независимую переменную x, искомую функцию y и ее первую производную y′, называется …
Вычислите предел по правилу Лопиталя lim (√(5 - x) - 2) / (√(2 - x) - 1), x⟶1
Общий член последовательности 1 / (1 ⋅ 3), 2 / (3 ⋅ 5), 3 / (5 ⋅ 7), 4 / (7 ⋅ 9), … имеет вид …
Найдите значение выражения ((a + 1)² / (a² - 1) - 1) ⋅ (1 - a / (a + 1)) при a=2
Вычислите предел по правилу Лопиталя lim (3x² + 2x - 1) / (-x² + x + 2), x⟶-1
Найдите производную функции y=ln sin x
Уравнение y” - y’ - 3y = 0 является …
Найдите предел lim (3n² + n - 1) / (2n² + 3), n⟶∞
Найдите общее решение уравнения y' - y / x = x
Уравнение вида P1(x)Q1(y)dx + P2(x)Q2(y)dy =0 является …
Найдите точку перегиба кривой y = 1/3 ⋅ x³ - x
Целыми называются …
Найдите ∫ xe^(x²)dx
Укажите уравнение параболы с вершиной в точке O и фокусом F(4; 0)
Эти вопросы в других коллекциях
Характеристики ответов (шпаргалок) к экзамену
Тип
Коллекция: Ответы к экзамену
Предмет
Учебное заведение
Вариант
Теги
Просмотров
1037
Качество
Идеальное компьютерное
Количество вопросов

❓ Как копировать вопросы во время теста в Синергии?
Отзывы
Отзыв
Зачет



















