Лабораторная работа 3: Численное интегрирование и дифференцирование вариант 15
Описание
Задача 1.
Найти приближенные значения интеграла и производной , используя указанные в индивидуальном варианте методы. Организовать серию расчетов с шагами . Сделать выводы о порядке точности и обусловленности методов. 
Задача 2.
Повторить расчет интеграла из Задачи 1 с помощью квадратурной формулы Ньютона-Котеса высокого порядка точности, указанной в индивидуальном варианте. Заполнить соответствующую таблицу (табл. 1). Сравнить результаты с результатами Задачи 1 (с учетом порядков точности использованных формул).
Сделать выводы: пользуясь результатами вычислений, показать, что расчет подтверждает порядок точности формулы Ньютона-Котеса; а также показать, в чем проявилось преимущество одной из двух квадратурых формул (из задач 1 и 2) над другой.
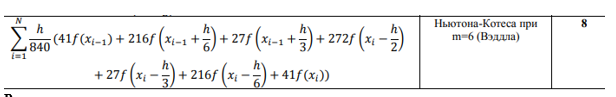
НИУ «МЭИ» 
brff
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
