Для студентов ИДДО НИУ «МЭИ» по предмету Теория вероятностей и математическая статистика (ТВиМС)Итоговый тестИтоговый тест
5,0052
2024-01-152025-01-01СтудИзба
Итоговый тест АТТ по предмету Теория вероятностей и математическая статистика
Ответы к экзамену АТТ: Итоговый тест
Описание
Итоговый тест АТТ по предмету Теория вероятностей и математическая статистика, решённый на 100%. Оценка 5
Вопросы из теста:
Показать/скрыть дополнительное описание
Вопросы из теста:
| 1 | Сочетаниями из n элементов по m в каждом называются такие комбинации, |
| 2 | Выборочная средняя распределения (ni – частота) равна: |
| 3 | Число размещений из n элементов по m в каждом вычисляется по формуле: |
| 4 | Дана выборка x = (x1, x2,…xn). Несмещенную оценку дисперсии этой выборки можно найти по формуле: |
| 5 | Вероятность того, что при n испытаниях событие А произойдет m раз, определяется по формуле Бернулли (q = 1 – p): |
| 6 | Если в схеме Бернулли р – малая величина и λ = np, то вероятность Pn;m того, что при n испытаниях событие А произойдет m раз можно найти по приближенной формуле: |
| 7 | Дисперсия случайной величины X определяется формулой: |
| 8 | Выборка задана в виде распределения частот: Тогда медиана этого вариационного ряда равна: |
| 9 | Чему равно среднее квадратическое отклонение случайной величины X, если случайная величина X характеризуется рядом распределения: |
| 10 | Выборка задана в виде распределения частот: Тогда среднее значение выборки равно: |
| 11 | Число сочетаний из n элементов по m вычисляется по формуле: |
| 12 |  |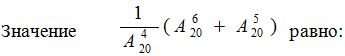
| 13 | Средний стаж работы рабочих АО составил 5 лет. Дисперсия стажа работы 4 года. Чему равен коэффициент вариации? |
| 14 | Среднее квадратическое отклонение – это: |
| 15 | Случайная величина, распределена по показательному закону f(x)=λe-λx. Произведена выборка, среднее значение которой равно 10. Тогда параметр λ оценивается числом: |
| 16 | Случайная величина X характеризуется рядом распределения: Тогда математическое ожидание случайной величины X равно: |
| 17 | Коэффициент корреляции двух случайных величин X и Y принимает значения: |
| 18 | Распределение дискретной случайной величины X имеет вид: Математическое ожидание случайной величины M(x) равно: |
| 19 | Ковариация между выборками x = (x1, x2,…xn) и y = (y1, y2,…,yn), вычисляется по формуле: |
| 20 | Магазин при осмотре партии товара А обнаружил в этой партии 2% брака. Дисперсия этого альтернативного признака (бракованного товара) равна |
Итоговый тест АТТ по предмету Теория вероятностей и математическая статистика.
Характеристики ответов (шпаргалок) к экзамену
Учебное заведение
ИДДО НИУ «МЭИ» Семестр
Номер задания
Просмотров
18
Качество
Идеальное компьютерное
Размер
894,95 Kb
Список файлов
Теория вероятностей и математическая статистика атт.docx
Алёна Руденко
alena.rudenko.88
15 января 2024 в 17:25
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
