ДЗ: Типовик-2 Вариант 1
Описание
ТИПОВОЙ РАСЧЕТ No2 «Математическое программирование»
Задачa 1. Решить задачу коммивояжера (на минимум) с матрицей затрат
Вар. | a | b | c | Вар. | a | b | c | Вар. | a | b | c |
1 | 6 | 5 | 4 | 11 | 4 | 3 | 5 | 21 | 7 | 3 | 5 |
2 | 4 | 1 | 3 | 12 | 5 | 5 | 2 | 22 | 6 | 1 | 8 |
3 | 3 | 2 | 4 | 13 | 8 | 4 | 7 | 23 | 3 | 3 | 3 |
4 | 4 | 4 | 1 | 14 | 5 | 1 | 6 | 24 | 8 | 2 | 2 |
5 | 7 | 4 | 5 | 15 | 2 | 2 | 2 | 25 | 6 | 4 | 5 |
6 | 5 | 2 | 4 | 16 | 6 | 3 | 3 | 26 | 5 | 2 | 5 |
7 | 1 | 1 | 1 | 17 | 6 | 7 | 8 | 27 | 1 | 5 | 3 |
8 | 3 | 4 | 1 | 18 | 6 | 2 | 4 | 28 | 5 | 4 | 3 |
9 | 7 | 6 | 5 | 19 | 2 | 1 | 4 | 29 | 5 | 3 | 4 |
10 | 6 | 2 | 6 | 20 | 7 | 5 | 3 | 30 | 4 | 4 | 4 |
Задача 2. Максимизировать функцию полезности
при ограничениях
Вар. | | | | Вар. | | | | Вар. | | | |
1 | 3 | 1.5 | 1 | 11 | 3 | 2 | 1.5 | 21 | 2 | 1.5 | 1 |
2 | 3 | 2.5 | 2.5 | 12 | 1.6 | 1.3 | 1.2 | 22 | 5 | 4 | 3 |
3 | 2 | 1.5 | 0.7 | 13 | 0.9 | 0.8 | 0.1 | 23 | 1 | 0.5 | 0.1 |
4 | 6 | 5 | 1 | 14 | 2 | 1.6 | 1.4 | 24 | 1.5 | 1.5 | 1 |
5 | 0.6 | 0.5 | 0.1 | 15 | 4 | 3.5 | 3 | 25 | 1 | 0.8 | 0.5 |
6 | 3 | 2 | 0.9 | 16 | 1 | 0.9 | 0.2 | 26 | 2 | 1.5 | 1.5 |
7 | 0.8 | 0.6 | 0.5 | 17 | 1.5 | 1.2 | 0.2 | 27 | 5 | 4 | 2 |
8 | 2 | 1.5 | 0.5 | 18 | 0.5 | 0.4 | 0.3 | 28 | 2 | 1.6 | 1.2 |
9 | 6 | 3 | 3 | 19 | 0.4 | 0.3 | 0.2 | 29 | 3 | 3 | 3 |
10 | 1.4 | 0.9 | 0.9 | 20 | 3 | 2.5 | 2 | 30 | 3 | 3 | 2.5 |
Задача 3. Для данного частично ориентированного графа (рис.1) найти:
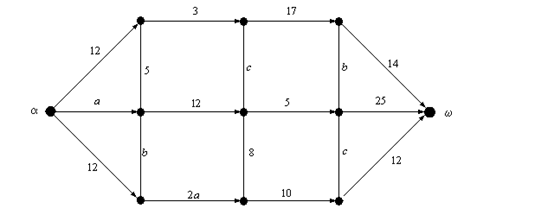
а) Кратчайший путь из источника в сток.
б) Максимальный поток и минимальный разрез.
По вертикальным ребрам (без стрелок) возможно движение в любом направлении. Значения параметров a, b, c взять из таблицы.
Вар. | a | b | c | Вар. | a | b | c | Вар. | a | b | c |
1 | 6 | 1 | 6 | 11 | 15 | 5 | 15 | 21 | 10 | 5 | 9 |
2 | 15 | 9 | 9 | 12 | 6 | 1 | 9 | 22 | 15 | 1 | 6 |
3 | 10 | 5 | 15 | 13 | 10 | 9 | 6 | 23 | 6 | 1 | 12 |
4 | 15 | 1 | 6 | 14 | 6 | 5 | 12 | 24 | 10 | 9 | 12 |
5 | 6 | 5 | 15 | 15 | 15 | 5 | 9 | 25 | 15 | 1 | 9 |
6 | 10 | 1 | 9 | 16 | 10 | 9 | 15 | 26 | 10 | 5 | 6 |
7 | 15 | 9 | 6 | 17 | 6 | 9 | 9 | 27 | 6 | 5 | 9 |
8 | 10 | 5 | 12 | 18 | 15 | 5 | 6 | 28 | 15 | 1 | 15 |
9 | 6 | 1 | 15 | 19 | 10 | 1 | 6 | 29 | 6 | 9 | 6 |
10 | 15 | 9 | 1 | 20 | 6 | 5 | 6 | 30 | 10 | 1 | 12 |
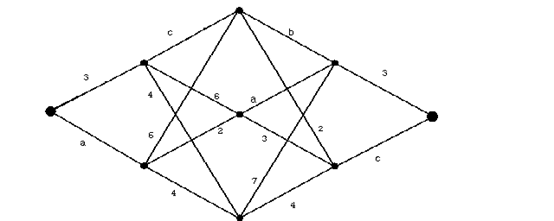
Задача 4. Найти максимальный путь в слоистом графе (рис.2).
Значения параметров a, b, c взять из таблицы задачи 1.
Задача 5. В рюкзак объема V=7 кладут N=5 групп предметов. Объемы,
веса и количество предметов в каждой группе приведены в таблице.
Группа | 1 | 2 | 3 | 4 | 5 |
Объем | 1 | 2 | 3 | v | 1 |
Вес | 2 | 3 | m | 4 | 1 |
Кол-во | 1 | n | 3 | 1 | 2 |
Максимизировать общий вес рюкзака.
Вар. | v | m | n | Вар. | v | m | n | Вар. | v | m | n |
1 | 1 | 4 | 1 | 11 | 2 | 2 | 2 | 21 | 3 | 3 | 3 |
2 | 1 | 2 | 1 | 12 | 1 | 6 | 2 | 22 | 4 | 1 | 2 |
3 | 3 | 5 | 2 | 13 | 3 | 2 | 2 | 23 | 2 | 1 | 1 |
4 | 3 | 3 | 4 | 14 | 2 | 2 | 1 | 24 | 1 | 2 | 3 |
5 | 2 | 1 | 3 | 15 | 3 | 4 | 2 | 25 | 4 | 4 | 2 |
6 | 2 | 3 | 2 | 16 | 1 | 1 | 1 | 26 | 1 | 1 | 3 |
7 | 1 | 3 | 1 | 17 | 3 | 2 | 2 | 27 | 2 | 2 | 3 |
8 | 3 | 1 | 2 | 18 | 4 | 2 | 3 | 28 | 4 | 2 | 2 |
9 | 3 | 1 | 1 | 19 | 2 | 3 | 4 | 29 | 3 | 3 | 2 |
10 | 4 | 1 | 3 | 20 | 3 | 2 | 1 | 30 | 2 | 5 | 2 |
 МГТУ им. Н.Э.Баумана
МГТУ им. Н.Э.Баумана



















