β∩γ = l, а т.к. образ пересечения равен пересечению образов, то g(β)∩g(γ) = g(l) и (g(β), g(γ)) =

(β, γ), если g – первого рода и

(g(β), g(γ)) = = -

(β, γ), если g– второго рода, поэтому

. (12)

3. Трансформация гомотетии движением

Рассмотрим . Пусть g(О)=А. Тогда по свойству неподвижных точек и двойных прямых, А – неподвижная точка преобразования , также мы имеем пучок неподвижных прямых в т. А, поэтому данное преобразование не может быть поворотной гомотетией или гомотетической симметрией. Следовательно, . Найдем коэффициент с, для этого рассмотрим точку М₁, пусть |М₁,A| = d.

Пусть g(М1) = М, мы знаем, что g(О)=А тогда по свойствам движения |МО| = d.

Пусть , по определению гомотетии |М₂О| = kd.

Пусть g(М₂) = М₃, по свойствам движения |М₃А| = kd. А т.к. при гомотетии все расстояния изменяются в одно и то же число раз, то с = k. Следовательно,

. (21)

4. Трансформация гомотетии гомотетией

Найдем сначала композицию двух гомотетий , для этого рассмотрим вектор . По свойству гомотетии, , а .

Рассмотрим первый случай, когда lk = 1, тогда мы получили преобразование, при котором вектор перешел сам в себя, а это параллельный перенос _{. Найдем вектор , для этого найдем образ точки О при этой композиции.}

, а : . Тогда . Значит, композиция двух гомотетий при lk = 1 есть параллельный перенос на вектор .

. (22)

Рассмотрим второй случай, когда lk ≠ 1. Найдем неподвижные точки этого преобразования. Пусть точка М – неподвижная, тогда если , а , то М = D, значит, . Но . Т.к. и , то

. Тогда . Т.к. lk ≠ 1, то выразим вектор : . Значит, у данного преобразования только одна неподвижная точка М, причем

, следовательно, точки O, Q, M лежат на одной прямой.

Докажем теперь, что данное преобразование будет гомотетией с центром в т. М и коэффициентом lk. Возьмем произвольную точку Е, пусть , а . Докажем, что (рис. 2). Разложим векторы и по векторам и . По правилу треугольника, , а . Ранее мы выразили вектор через вектор

: , тогда вектор

выражается через вектор следующим образом: . Вектор при гомотетии переходит в вектор , тогда . Значит, . Теперь приведем подобные слагаемые и разложим вектор по векторам и , после этого получим . Вектор при гомотетии 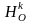переходит в вектор , значит, , а вектор вновь выразим через , тогда . Приведем подобные слагаемые, получим

. По правилу треугольника

, следовательно . Таким образом, мы показали, что преобразование произвольную точку E переводит в точку G такую, что , следовательно, это преобразование – гомотетия с центром в точке М и коэффициентом lk.

. (23)

Сейчас найдем преобразование . , а это по формуле (23) равняется , . Далее применяя формулу (23), получаем

, . Выразим вектор

через вектор . По правилу треугольника, . Мы уже знаем, что , тогда . Приведем подобные слагаемые, получим

. Так как , то . Значит,

. Таким образом,

^. (24)

5. Трансформация движения гомотетией

5.1. Трансформация осевой симметрии гомотетией

Рассмотрим . По теореме о неподвижных точках, прямая – неподвижная прямая преобразования , значит, это осевая симметрия с осью m.

. (25)

5.2. Трансформация параллельного переноса гомотетией

, но , . [1] Тогда , что по формуле (22) равняется . Следовательно,

. (26)

5.3. Трансформация произвольного движения гомотетией

Рассмотрим . По теореме о неподвижных точках, неподвижными точками преобразования являются образы неподвижных точек движения f. Докажем, что это – движение. . Рассмотрим точки А и L, |AL| = d. Пусть при гомотетии они переходят соответственно в точки В и М, тогда |BM| = d/k. При движении f точки В и М переходят соответственно в точки С и N, тогда |CN| = d/k, т.к. движение сохраняет расстояния между точками. Пусть при гомотетии 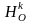точки С и N переходят соответственно в точки D и P, |DP| = kd/k = d. Мы получили, что преобразование сохраняет расстояния между точками, значит, это движение, неподвижными точками которого являются образы неподвижных точек движения f, а т.к. вид движения определяется его неподвижными точками, то - движение того же вида, что и f.

6. Трансформация подобия гомотетией

Рассмотрим , где f – подобие. Известно, что подобие – это композиция движения и гомотетии, тогда , а это, по формулам (2), равняется . Как было доказано в 5.3, - движение того же вида, что и g, а по формуле (24) . Следовательно, - подобие того же вида, что и f. Если f , то

. (27)

7. Трансформация движения подобием

Пусть подобие – это композиция движения g и гомотетии 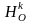, то движение f под подобием – это . В силу ассоциативности композиции преобразований, . По доказанному в п. 5.3 = f₁ - движение того же вида, что и f, а его неподвижные точки – образы неподвижных точек движения f при гомотетии 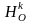. Тогда . Но f₁^g = f₂ – движение того же вида, что и f₁, а его неподвижные точки – образы неподвижных точек движения f₁ при движении g. Тогда - движение того же вида, что и f, а его неподвижные точки – образы неподвижных точек движения f при подобии .

8. Трансформация подобия движением

Пусть подобие – это композиция движения f и гомотетии , тогда подобие под движением g по формулам (2) есть . f^g = f₁ – движение того же вида, что и f, а его неподвижные точки – образы неподвижных точек движения f при движении g, а по формуле (21) . Тогда , а это подобие.

. (28)

9. Трансформация гомотетии подобием

Рассмотрим . В силу ассоциативности композиции преобразований, . По формуле (24), , . Тогда (по формуле (21)). Таким образом,

. (29)

10. Трансформация подобия подобием

Подобие φ под подобием ψ . По формулам (2), . - движение того же вида, что и f, а его неподвижные точки – образы неподвижных точек движения f при подобии ψ. По формуле (29), . Тогда

, (30)

где ξ - подобие такое, что , , а h – движение того же вида, что и f, а его неподвижные точки – образы неподвижных точек движения f при подобии ψ.

11. Трансформация движения аффинным преобразованием

11.1. Трансформация параллельного переноса аффинным преобразованием

Р ассмотрим произвольную точку М, найдем ее образ при преобразовании . При преобразовании g^-1 она переходит в точку М₁ (рис. 3), которая при параллельном переносе прейдет в точку М₂, , далее М₂ при преобразовании g перейдет в точку М₃. Заметим, что вектор при преобразовании g перейдет в вектор , значит, вся трансформация есть параллельный перенос на вектор .

, (31)

где .

11.2. Трансформация центральной симметрии аффинным преобразованием

Р

g(O)

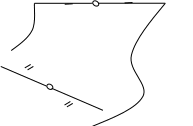
ассмотрим произвольную точку М, найдем ее образ при преобразовании 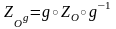. При преобразовании g^-1 она переходит в точку М₁ (рис. 4), которая при центральной симметрии Z_O прейдет в точку М₂, О – середина М₁М₂, далее М₂ при преобразовании g перейдет в точку М₃. Заметим, что точка О при преобразовании g перейдет в середину отрезка ММ₃ (т.к. при аффинном преобразовании сохраняется принадлежность точек одной прямой и отношение расстояний между ними), а по теореме о неподвижной точке g(O) будет неподвижной точкой нового преобразования, значит, вся трансформация 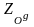есть центральная симметрия Z_g(O).

. (32)

11.2. Трансформация осевой симметрии аффинным преобразованием

Р ассмотрим произвольную точку М, найдем ее образ при преобразовании . При преобразовании g^-1 она переходит в точку М₁ (рис. 5), которая при осевой симметрии S_l прейдет в точку М₂, , О – середина М₁М₂, далее М₂ при преобразовании g перейдет в точку М₃. Заметим, что точка О при преобразовании g перейдет в середину отрезка ММ₃ (т.к. при аффинном преобразовании сохраняется принадлежность точек одной прямой и отношение расстояний между ними), и ее образ – О₁ – будет лежать на образе прямой l при преобразовании g - g(l). По теореме о неподвижных прямых, прямая g(l) будет неподвижной прямой нового преобразования. Заметим также, что если при осевой симметрии прямые, соединяющие точки с их образами, были параллельны, то и после трансформации они будут параллельны и наклонены под одним и тем же углом к прямой g(l), значит, вся трансформация есть косая симметрия S_g(l).

. (33)

12. Трансформация гомотетии аффинным преобразованием

Р ассмотрим произвольную точку М, найдем ее образ при преобразовании . При преобразовании g^-1 она переходит в точку М₁ (рис. 6), которая при гомотетии 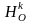прейдет в точку М₂, , далее М₂ при преобразовании g перейдет в точку М₃. Заметим, что точка О при преобразовании g перейдет в точку О₁ на прямой ММ₃, причем (т.к. при аффинном преобразовании сохраняется принадлежность точек одной прямой и отношение расстояний между ними), а по теореме о неподвижной точке точка О₁ будет неподвижной при новом преобразовании, значит, вся трансформация есть гомотетия .

. (35)

13. Трансформация аффинного преобразования гомотетией

Далее будем предполагать, что аффинные преобразования g и g^-1 заданы аналитически.

g: g^-1: где образы начала координат и базисных векторов при преобразовании g имеют координаты: O’(d₁, d₂, d₃), (a₁, a₂, a₃), (b₁, b₂, b₃), (c₁, c₂, c₃), а при преобразовании g^-1 O’’(n₁, n₂, n₃), (k₁, k₂, k₃), (l₁, l₂, l₃), (m₁, m₂, m₃).