48134 (Построение ОВС для решения формулы)

Содержание

1. Выбор варианта

1.1 Вычисление числа К

1.2 Выбор параметров варианта

2. Структура вычислительного процесса алгоритмы вычислений

2.1 Структура вычислительного процесса

2.2 Последовательность обработки операндов

2.2.1 Обработка числа А

2.2.2 Обработка числа В

2.2.3 Обработка числа С

3. Схемы ОВС

3.1 Обозначения на схемах

3.1 Схема участка ОВС для вычисления числа А

3.2 Схема участка ОВС для вычисления числа В

3.3 Схема участка ОВС для вычисления числа С

4. Временные диаграммы

4. Временные диаграммы

4.1 Таблицы временных диаграмм

5. Программирование ОВС

5.1 Коды команд ОЭ

5.2 Схема цепей программирования

Заключение

1. Выбор варианта

1.1 Вычисление числа К

Для предупреждения повторов, определение варианта проводится по формуле, которая учитывает количество групп на потоке и количество человек в группе. Формула выглядит следующим образом:

К= (n-1) ×30+m (1.1.1)

где n - номер группы студента, а m - номер студента в группе.

К= (2-1) ×30+12=30+12=42.

1.2 Выбор параметров варианта

Для решения задачи необходимы начальные условия, а именно:

формула вычисления С;

системы счисления для операндов А и В;

код, в котором происходят вычисления;

направления входа и выхода чисел;

максимальное количество тактов программирования.

Формула вычисления определяется параметром X. Параметр Х равен остатку от деления числа К на 11, т.е.

Х=К mod 11 (1.2.1)

Для К=42, Х=9. Так как Х=9, то согласно табл.1 число С вычисляется по формуле C=7|A-B|/4.

Y=K mod 3 (1.2.2) Z=K mod 7 (1.2.3)

Системы счисления для операндов А и В зависят от параметров Y и Z, вычисляемые по формулам (1.2.2) и (1.2.3) соответственно. Следовательно, по таблицам 2 и 3 можно определить Y и Z. Для выше упомянутого варианта Y=0 и Z=0, т.е. операнд А поступает на вход устройства кодированый в двоично-пятиричной системе счисления, а операнд В - в двоично-девятиричной.

Таблица 1. Таблица 2. Таблица 3.

Х	Формула вычисления С		Y	Система счисления		Z	Система счисления
0	3|A/2-B/4|		0	2-5		0	2-9
1	|3A/4-B|		1	2-6		1	2-10
2	|A-5B/4|		2	2-7		2	2-11
3	|3A-B|/4					3	2-12
4	|3A-4B|					4	2-13
5	|5A-3B|/2					5	2-14
6	5|A-2B|/4					6	2-15
7	|5A/2-2B|
8	|7A/4-2B|
9	7|A-B|/4
10	|6A-5B|

В связи с тем, что в формуле используется вычитание необходимо проводить вычисления в обратном или в дополнительном кодах. Так как К - чётное число, вычитание проводится в дополнительно коде 1.

При помощи параметра V, определяются направления входов операндов и выхода результата.

Для этого используется формула (1.2.4), причём число V представляется в двоичном коде.

V=K mod 64 (1.2.4)

Для сорок второго варианта V=42=1010102, причём следует учесть, что направления движения чисел читаются с право налево, т.е. V=10 10 102, и 00-это юг, 01-запад, 10-север, 11-восток. С В А

Устройство должно выполнить вычисление за минимальное время, т.е. за минимальное количество тактов. Частично этого можно достичь, сократив время программирования ОЭ.

Т£ (X+Y+Z+6) ×16 (1.2.5)

При К=42, накладывается следующее ограничение тактов программирования:

T£ (9+0+0+6) ×16=15×16= 240.

Из предыдущих вычислений следует, что С вычисляется по формуле С=7|A-B|/4, число А двоично-пятиричное и поступает с севера, В - двоично-девятиричное и так же поступает с севера, вычитание производится в дополнительном коде, результат выдаётся на север и количество тактов программирования не превышает двухсот сорока.

2. Структура вычислительного процесса алгоритмы вычислений

2.1 Структура вычислительного процесса

В

ОВС вычисления могут производиться ОЭ как последовательно, так и параллельно. В дальнейшем будут использоваться оба способа. Поэтому для наглядности происходящих процессов ниже на рис.1 приведена структура вычислительного процесса.

Рис.1.

2.2 Последовательность обработки операндов

2.2.1 Обработка числа А

Обработка числа заключается в том, что необходимо число перевести из двоично-кодированного вида в двоичный, а так же преобразовать его в дополнительный код, В таком виде оно пригодно для дальнейшего использования.

В начальных условиях указано, что операнд А можно считать положительным числом, а это означает, что прямой код числа совпадает с дополнительным.

Таким образом, обработка числа А состоит в выделении старшей тетрады, выделении младшей тетрады, умножении H на пять и сложении с L. Подробно эти действия представляет алгоритм на рис.2.

Число А2-5 поступает с севера. Выделение старшей тетрады производится путём логического умножения А2-5 на константу вида 111100002 или F016. Это наглядно иллюстрирует пример:

Рис.2

Младшая тетрада выделяется аналогичным способом:

Двоичное число находится по формуле (2.2.1 1)

A2=Hn×S+L (2.2.1 1)

где S-система счисления двоично-кодированного числа, L-его младшая тетрада, а Hn-нормализированная старшая тетрада двоично-кодированного числа:

а8 а7 а6 а5 0 0 0 0=H

0 0 0 0 а8 а7 а6 а5=Hn

Для сорок второго варианта формула (2.2.1 1) выглядит следующим образом: А2=5×Hn+L

Процедура умножения старшей тетрады на пять может быть представленной в виде: 5Hn=Hn+4Hn

2.2.2 Обработка числа В

Операнд В обрабатывается аналогично операнду А, за исключением некоторых особенностей.

Рис.3

Число В поступает кодированное в двоично-девятиричной системе счисления, поэтому старшая тетрада умножается на девять, причём, поступающее число В отрицательно и его прямой код не совпадает с дополнительным. Следовательно, операнд В необходимо перевести в дополнительный код. Это осуществляется путём вычитания единицы с последующим инвертированием. Вычесть единицу можно путем сложения числа с константой вида 1 1 1 1 1 1 1 12 1.

Всё выше перечисленное показано на рис.3.

2.2.3 Обработка числа С

Для получения числа С необходимо модуль разности чисел А2 и В2 умножить на семь и разделить на четыре. Сумма чисел Адп и Вдп даст результат так же в дополнительном коде. Получить прямой код результата, который будет равен разности чисел А2 и В2, можно при помощи арифметического сложения Сдп с его же знаковыми разрядами:

В
ычисление прямого кода из обратного производится путём сложения по модулю два числа Соб так же с его знаковыми разрядами:



Умножение на семь осуществляется следующим способом: 7C= 4C+2C+C. А деление на четыре путём логического умножения на константу 1 1 1 1 1 1 0 02 и задержкой на два такта.

Рисунок 4 представляет схему алгоритма вычисления числа С.

Схема алгоритма вычисления числа С

Рис.4.

3. Схемы ОВС

3.1 Обозначения на схемах

Для удобства применения и простоты восприятия, операции условно обозначаются значками:

&-логическое умножение;

&-логическое умножение с инверсией;

-логическое сложение;

-сумма по модулю два;

+-арифметическое сложение;

T-условное запоминание;

GC-генерация константы;

DD-задержка на девять тактов.

Кроме этого, пунктирной линией показаны транзиты, стрелками-направления движения чисел. Так же указываются такты задержки и такты выходов первых бит чисел.

Номера ОЭ состоят из двух цифр: первая-номер микросхемы, вторая-номер ОЭ в микросхеме.

3.2 Схема участка ОВС для вычисления числа А

На схеме ОВС непосредственно указывается, как будут работать ОЭ.

На рис.5 представлена схема ОВС для вычисления двоичного числа А.

Число А2-5 поступает на двенадцатый элемент, он выполняет операцию логического умножения константы F016 и А2-5, а так же транзит числа на запад с задержкой на два такта.

Тринадцатый элемент складывает число само с собой и задерживает его на два такта, таким способом достигается задержка числа на три такта.

Р
ис.5

Э

L

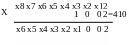
лементы четырнадцать и пятнадцать позволяют умножить старшую тетраду на пять, при этом используется свойство двоичных чисел при умножении на константу вида 2:

Взяв число на два такта раньше, получается число умноженное на четыре. Аналогично происходит умножение на два, восемь, шестнадцать и т.д. .

На шестнадцатом элементе происходит выделение младшей тетрады. Девятнадцатый ОЭ производит сложение старшей и младшей тетрад и выдаёт двоичный результат на запад. Одиннадцатый и тридцать четвёртый ОЭ генерируют константы.

3.3 Схема участка ОВС для вычисления числа В

Участок ОВС для обработки числа В работает аналогично участку, обрабатывающему число А, за исключением трёх ОЭ, позволяющих переводить двоичное число в дополнительный код.

Рис.6.

На Рис.6 перевод числа в дополнительный код осуществляется на трёх ОЭ. Тридцать первый ОЭ генерирует константу FF16, а тридцать второй складывает её с двоичным чсислом. Тридцать пятый ОЭ выполняет операцию логического умножения, причём, число умножается само на себя, чем достигается сохранение его начального значения, затем инвертирует его. Таким образом совершается перевод числа в дополнительный код в ОВС.

3.4 Схема участка ОВС для вычисления числа С

Рис.7

Тридцать восьмой ОЭ складывает поступающие числа А и В. Тридцать девятый ОЭ производит задержку числа на девять тактов и подаёт на юг тридцать шестого ОЭ. В тот такт, когда на тридцать шестой ОЭ поступает число Сдп с юга, с запада появляются знаковые разряды числа Сдп. Таким образом выполняется арифметическое сложение числа с его знаковыми разрядами. Такая операция может быть совершена благодаря свойству ОВС что, после чиса (после седьмого бита) следуют знаковые разряды этого числа, т.е. восьмой, девятый, десятый и т.д. биты знаковые разряды.

Аналогичным способом происходит сложение по модулю два числа Соб с его знаковыми разрядами на сорок четвёртом и сорок седьмом ОЭ. На сорок первом, сорок втором, сорок пятом и сорок восьмом ОЭ выполняется умножение числа Спр на семь. А сорок шестой и сорок девятый позволяют делить число на четыре.