Аналитическая геометрия ДЗ 2. Вариант 3
Описание
Факультеты: СМ, РК, ИУ10
1 семестр 1 курс
Зачтено на максимум
👉 ДЗ 2 включает:задания №1-4. 👈
📃УСЛОВИЕ

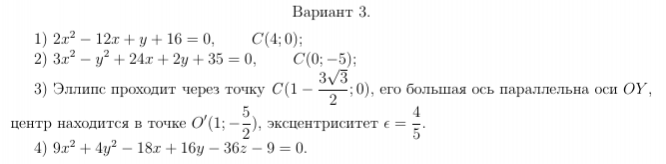
Состав файла:
- Фото решений заданий №1-4(с графиками)
- Графики решений и ссылки на них в Desmos
Спасибо за покупку)
У тебя все получиться, верь в себя 😜Показать/скрыть дополнительное описание
МГТУ им Н.Э Баумана. Бауманка. Бомонка. ДЗ ангем. ангеом. Вариант 3. ДЗ1. ДЗ_1. ДЗ 1. ДЗ2. ДЗ_2. ДЗ 2. СМ. РК4. ИУ10. ДЗ1 решение готовое, фото, условие.”Векторная алгебра и аналитическая геометрия” CM,ФН 1 курс 1 семестр Домашнее задание. ДЗ1. ДЗ1.1. ДЗ1.2. ДЗ_1.1. ДЗ_1.2. ДЗ_1. ДОМАШНЕЕ ЗАДАНИЕ 1 курс 1 семестр ”КРИВЫЕ И ПОВЕРХНОСТИ ВТОРОГО ПОРЯДКА” В задачах 1 − 2 заданное уравнение линии второго порядка привести к каноническому виду и построить кривую в системе координат OXY . В задаче 3 по приведенным данным найти уравнение кривой в системе координат OXY . Для задач 1 − 3 указать: 1) канонический вид уравнения линии; 2) преобразование параллельного переноса, приводящее к каноническому виду; 3) в случае эллипса: полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки C до фокусов; в случае гиперболы: полуоси, эксцентриситет, центр, вершины, фокусы, расстояния от точки C до фокусов, уравнения асимптот; в случае параболы: параметр, вершину, фокус, уравнение директрисы, расстояния от точки C до фокуса и директрисы; 4) для точки C проверить свойство, характеризующее данный тип кривых как геометрическое место точек.
В задаче 4 указать преобразование параллельного переноса, приводящее данное уравнение поверхности к каноническому виду, канонический вид уравнения поверхности и тип поверхности. Построить поверхность в канонической системе координат OXY Z. Вариант 3. 1) 2x 2 − 12x + y + 16 = 0, C(4; 0); 2) 3x 2 − y 2 + 24x + 2y + 35 = 0, C(0; −5); 3) Эллипс проходит через точку С (1 − 3 √ 3 2 ; 0), его большая ось параллельна оси OY , центр находится в точке O 0 (1; − 5 2 ), эксцентриситет ² = 4 5 . 4) 9x 2 + 4y 2 − 18x + 16y − 36z − 9 = 0.
 МГТУ им. Н.Э.Баумана
МГТУ им. Н.Э.Баумана


















