Ответы к экзамену: Аттестационный тест по курсу "Линейная алгебра" (ПЯ) (ИДДО)

Аттестационный тест по курсу "Информатика"
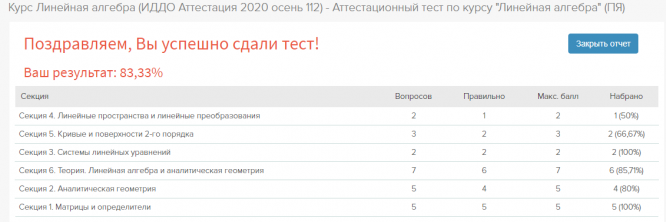
Общий балл теста - 83%
Файл содержит скриншоты 24 вопросов с ответами из 24 на аттестационный тест по курсу "Линейная алгебра", в случайном порядке


Вопросы:

Уравнение x2 – 2y2 = 1 задает:

Ранг матрицы A равен:

Уравнение x2 + y2 – z2 = 0 задает:

Смешанное произведение векторов - это

Скалярное произведение векторов - это

Может ли конечномерное линейное пространство не иметь базиса?

Если базис линейного пространства состоит из 3-х векторов, то размерность этого пространства равна

Может ли линейный оператор иметь ровно два различных собственных вектора?

Могут ли матрицы линейного оператора в двух различных базисах быть одинаковыми?

Верно ли, что ранг матрицы - это всегда число строк в матрице?

Дано: →a = (2;0;1), →b = (0;1;0). Найти угол между векторами.

Дано: →a = (1;2;0), →b = (3;0;1). Найти длину вектора →a × →b.

Написать уравнение прямой, проходящей через точку A(1;2;3) параллельно вектору →a = (–2;3;0).

Можно ли умножить матрицу A на матрицу B?

Существует ли матрица, не являющаяся единичной, обратная к которой совпадает с ней самой?

Дано: A, B. Найти A - 2B.

Найти определитель матрицы A.

Для матрицы A найти транспонированную:

Найти размерность линейного пространства L.

Уравнение x – y2 = 0 задает:

Решить систему уравнений методом Крамера:

Дано: →a = (1;3;5), →b = (2;6;0). Являются ли данные вектора коллинеарными?

Лежат ли точки A(1;2;0), B(3;3;1), C(5;4;2) на одной прямой?

Найти размерность (над R) пространства решений системы уравнений: