Задача 2: Расчет иерархической древовидной конфигурации сети вариант 4
Описание
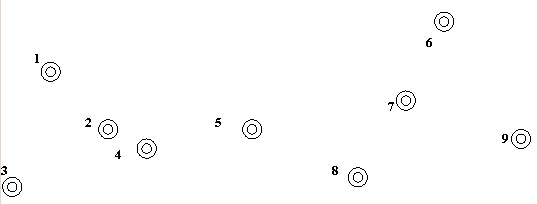
Рис. 1
Даны узлы, расположенные как показано выше на рис. 1, заданы взвешенные расстояния, представленные в матрице М.
Матрица M расстояний между узлами
0 | 35 | 50 | 25 | 45 | 40 | 30 | 26 | 70 |
35 | 0 | 15 | 11 | 10 | 55 | 50 | 48 | 90 |
50 | 15 | 0 | 25 | 24 | 70 | 75 | 60 | 100 |
25 | 11 | 25 | 0 | 21 | 45 | 40 | 35 | 60 |
45 | 10 | 24 | 21 | 0 | 65 | 60 | 55 | 100 |
40 | 55 | 70 | 45 | 65 | 0 | 12 | 30 | 40 |
30 | 50 | 75 | 40 | 60 | 12 | 0 | 18 | 28 |
26 | 48 | 60 | 35 | 55 | 30 | 18 | 0 | 40 |
70 | 90 | 100 | 60 | 100 | 40 | 28 | 40 | 0 |
Задано, что вес каждого узла равен 1. Суммарный вес центра группы уровня h = 2 равен 3, следовательно, каждая группа должна состоять из 3-х узлов нижнего уровня. Суммарный вес центра группы уровня h = 3 равен 9. Требуется построить древовидную иерархическую сеть минимальной длины, обеспечивающую многоуровневое покрытие исходных узлов.
Исходные данные для расчета следующие:
N = 9; количество узлов,
Zi = 1; веса узлов, которые равны количеству информации, передаваемой узлом за единицу времени,
Пh = 1 = 3; пропускные способности центров групп h = 1,
Пh = 2 = 9, пропускные способности центров групп h = 2.
ИДДО НИУ «МЭИ» 
Сергей77
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
