Задача 3: Колебания вариант 18

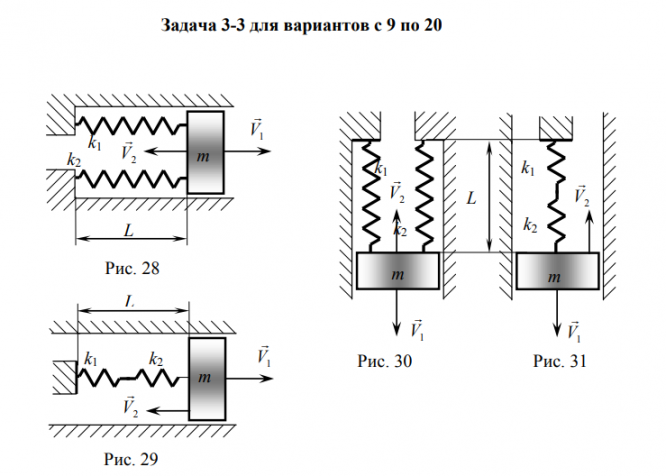
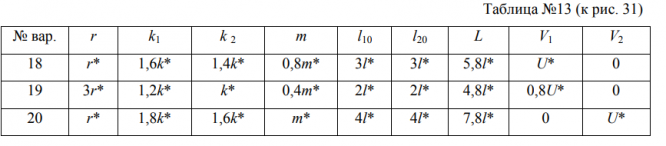
Для конкретной колебательной системы (КС), представленной на соответствующем рисунке, необходимо: 1. Вывести дифференциальное уравнение малых свободных затухающих колебаний, если сила сопротивления движению тела КС пропорциональна скорости, т.е. F r V    , где r - коэффициент сопротивления. 2. Определить круговую частоту 0 и период T0 свободных незатухающих колебаний. 3. Найти круговую частоту  и период T свободных затухающих колебаний. 4. Вычислить логарифмический декремент затухания. Каждая колебательная система (КС), представленная на рис. 28, 29, 30, 31, состоит из шайбы массой m и двух упругих пружин, имеющих жесткости k1 и k2 . Движение КС происходит в окружающей среде с малыми вязкими свойствами (малым коэффициентом сопротивления r).

На рис. 28, 30 шайба колеблется под действием пружин, соединенных параллельно, а на рис. 29, 31 колебания происходят под действием пружин, соединенных последовательно. Массой пружин можно пренебречь. На рис. 28, 29 КС имеет горизонтальное расположение, а на рис. 30, 31 вертикальное расположение в поле силы тяжести. Длины 1-ой и 2-ой пружин в недеформированных состояниях равны l10 и l20. На рис.28, 30 L - длина каждой пружины в деформированном состоянии при t=0. На рис.29, 31 L - общая длина двух пружин в деформированном состоянии при t=0. Возможные векторы начальной скорости шайбы равны V1 , V2 . Шайбу, находящуюся в положении равновесия, смещают до расстояния L, а затем импульсом придают ей в начальный момент времени t=0 скорость V1 или V2 , в соответствии с заданием (см.

таблицы № 10 - 13). В результате КС приходит в колебательное движение. Физика дз 3 задача 3-3 мгту баумана  .