Шпаргалка (943761), страница 3
Текст из файла (страница 3)
Поскольку число рассеивателей линейно растет с температурой, так же ведет себя и сопротивление:
ρ~T, T>> TD
при температурах Т << TD полная частота электрон-фононного рассеяния уменьшается пропорционально Т3 ,a
:
ρ~T5, при T « TD
а б
Рис. 10.9. Диаграмма состояния сплавов, образующих твердые растворы с неограниченной растворимостью компонентов, схема расположения атомов Сu (черные) и Ni (белые) в решетках сплавов (а) и изменение физико-химических свойств в зависимости от состава (б)
Рис. 12.6. Зависимость удельного сопротивления ρδ (а) и температурного коэффициента удельного сопротивления αρδ (б) металлической пленки от ее толщины δ
Скин-эффект характеризуется глубиной проникновения электромагнитного поля в металлический проводник: чем выше частота поля, тем на меньшую глубину оно проникает в проводник. С увеличением глубины проникновения поля плотность тока уменьшается по экспоненте. Глубину, на которой амплитуда электромагнитной волны затухает в е раз (до -37%), называют глубиной проникновения поля ∆. Величина ∆ зависит от частоты напряжения ω, удельной электропроводности γ и магнитной проницаемости μ:
∆
 = 1/a = √ 2/ωγμoμ = √ƒπγμoμ, (12.10)
= 1/a = √ 2/ωγμoμ = √ƒπγμoμ, (12.10)
где а — коэффициент затухания электромагнитной волны; μo — магнитная постоянная
При изготовлении проволоки болванки сначала путем горячей прокатки превращают в катанку диаметром 8—18 мм, которую для
Рис.13.1. Зависимость предела прочности на разрыв σв, относительно удлинения перед разрывом ∆L/L и удельного сопротивления ρ меди марки Ml от температуры отжига (время отжига 1 час)
Таблица 13.5 Основные свойства сплавов высокого сопротивления
| Сплав | Плот- ность. Mг/м3 | Удельное сопротив- ление ρ, мкОм •м | ТКρ• 106 К-1 | Термо- ЭДС отно- ситель -но меди мкВ/К | Предельнодопустимая рабочая температура С | Предел прочности σв, МПа | Относительное удлинение при разрыве ,% | ||
| Манга- нин | 8,4 | 0.42-0,48 | 5-30 | 1-2 | 200 . | 450-600 | 10-15 | ||
| Конст- антан | 8,9 | 0,48-0,52 | -(5- 25) | 40-50 | 450-500 | 450-650 | 15-20 | ||
| Сплавы Системы Fe-Ni-Cr (нихромы): Х15Н60 Х20Н80 | 8,2-8,3 7,1-7,5 | 1,0-1,2 1,0-1,1 | 100-200 100-200 | ____ _____ | 1000 1100 | 650-700 650-700 | 22 20 | ||
| Сплавы системы Fe-Cr-Al (фехраль и хромаль): Х13Ю4 Х23Ю5 | 7,1-7,5 6,9-7,3 | 1,2-1,35 1,3-1,4 | 100-200 65 | ________ | 900 1200 | 700 800 | 20 10-15 | ||
ЭДС шумов резистора. Электроны в резистивном элементе находятся в состоянии хаотического теплового движения, в результате которого между любыми точками резистивного элемента возникает случайно изменяющееся электрическое напряжение и между выводами резистора появляется ЭДС тепловых шумов. Тепловой шум характеризуется непрерывным, широким и практически равномерным спектром. Величина ЭДС тепловых шумов определяется соотношением
E,=(4KTR∆f) 1/2, (2.16)
где К=1,38•10-23Дж/ К— постоянная Больцмана;
Т — абсолютная температура, К;
R — сопротивление, Ом;
∆f— полоса частот, в которой измеряются шумы.
При комнатной температуре (Т= 300 К)
E,=(1/8)*( R∆f) 1/2
Рис. 12.9. Схема образования контактной разности потенциалов (а) и термоэлектродвижущей силы (б)
Рис. 12.8 Потенциальный барьер на границе металл— вакуум:
1 — внешнее электрическое поле равно нулю (Е= 0); 2 — внешнее электрическое поле не равно нулю (Е = 0)
Зависимость сопротивления платиновых терморезисторов от температуры определяется следующими формулами:
R t = R0 (1 + At + Bt2) при 0 < t < 650°С;
Rt = R0 [1 + At + Bt2 + Ct3 (t -100)] при -200 < t < 0°C,
где Rt — сопротивление терморезистора при температуре t, °C; R0 — сопротивление при 0°С; А = 3,96847 х10-3 (0 o С) -1 ; В = -5,847 х10-7 (0 o С) -2 ; С = -4,22 х10-12 (0 o С) -4 .
Для измерения температуры наиболее распространены полупроводниковые терморезисторы типов КМТ (смесь окислов кобальта и марганца) и ММТ (смесь окислов меди и марганца). Термисторы имеют линейную функцию преобразования, которая описывается следующей формулой:
Rt = AeB/T,
где Т — абсолютная температура;
А — коэффициент, имеющий размерность сопротивления; В — коэффициент, имеющий размерность температуры.
Серийно выпускаются медно-марганцевые (тип ММТ) и кобальтово-марганцевые (тип КМТ) термисторы. На рис. 9.2 показаны зависимости сопротивления от температуры для термисторов этих типов и для сравнения — для медного терморезистора.
 Рис. 9.2. Зависимости сопротивления
Рис. 9.2. Зависимости сопротивления
от температуры для термисторов и медного
терморезистора
Основные характеристики терморезисторов
1. ВАХ — зависимость напряжения на терморезисторе от
тока, проходящего через него. Снимается в условиях теплового
равновесия с окружающей средой. На рис. 1.1 и 1.2 график (А)
соответствует терморезистору с отрицательным ТКС, (Б) — с
положительным.
Р
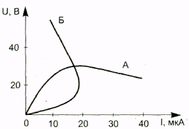 ис.1.1.Вольт-амперная характеристика терморезистора
ис.1.1.Вольт-амперная характеристика терморезистора
Температурная характеристика — зависимость R(T), сни
мающаяся в установившемся режиме. Принятые допущения: мас
штаб по оси R взят возрастающим по закону 10х, по оси Т
пропущен участок в интервале (0...223) К (см. рис. 1.2).
Рис. 9.4. Получение релейной характеристики в схеме с термистором
Рис. 8.4.1. Энергетические диаграммы твердого тела с указанием красной границы hν0 фотоэлектронной эмиссии
а б в г
Рис. 4.1. Зонная структура германия (а)
точки (100) — X, (111) — L и (110) — К на границе зоны при к = 2π/а и [100]-∆, [111] — Λ [110] — Σ внутри зоны. Центр зоны Бриллюэна, т. е. состояние k = 0, обозначают Г. Нижние индексы у букв характеризуют симметрию состояния и означают неприводимые представления, к которым принадлежит волновая функция в данной состояния в кристаллах условно можно разделить на слабо связанные («мелкие») и сильно связанные («глубокие») состояния. Эвергия связи мелкого центра существенно меньше ширины запрещенной зоны, а для глубокого она сравнима с шириной запрещенной зоны.
Волновой вектор k
Рис. 2.13. Электронная зонная структура Ge, расчитанная по методу псевдопотенциала.
Энергия в вершине заполненной валентной зоны принята равной нулю. В отличие от рис. 2.10 здесь использовано обозначение симметрии
для двойных групп [2.8]
Фиг. 2.15. Первая зона Бриллюэна решетки алмаза и решетки цинковой обманки, а также основные точки и линии симметрии [18].
Рис. 4.45. Схема опыта для измерения фотопроводимости
Рис. 9.9. Три конфигурации светодиодов:
а — полусфера; б — усеченная сфера (сфера Вейерштрассе); в — эллипсоид
Рис.9.7. Схематическое изображение плоского светодиода
Рис. 9.10. Спектры излучения светодиодов



































