Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

Для любого «полного» корневого поддерева g с корнем v дерева G (с корнем в ):

, где и – подмножество такое, что: , при этом (см. рис. 3.2.2).

Доказательство

Воспользуемся методом математической индукции:

1. m = 1:

Пусть , тогда . Тогда, учитывая утверждение 1.1, и , получим требуемое.

1. Пусть утверждение леммы верно для m = k, тогда:

2. Докажем теорему для m = k+1.

Мы имеем: , тогда:

Если и , то :

Из утверждения 3.2.1:

, но , т.е. , откуда , ч.т.д.

Теорема 3.3.1.3

«Нулевое» дерево ― бинарное дерево с точностью до петли в корне e_n.

Доказательство:

П

Рис. 3.3.3

усть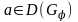 и, 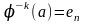тогда мы можем достроить его, пользуясь теоремой 3.3.1.2 до бинарного дерева с точностью до петли в корне e_n (см. рис. 3.3.3) Заметим, что n+1-го яруса быть не может т.к. тогда мы достраиваем этот ярус и получаем 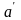такое, что 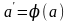но – противоречие.

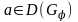Теорема 3.3.1.4

Все деревья (в том числе и примыкающие к каждой вершине произвольного цикла) будут иметь столько ярусов, сколько и «нулевое», причем будут иметь такую же структуру.

Более точно: дерево, притягиваемое каждой точкой каждого цикла графа состояний, изоморфно дереву, притягиваемому точкой e_n.

Доказательство:

Предположим «нулевое» дерево состоит из n ярусов тогда:

1. Если наше дерево состоит менее чем из n ярусов, то, пользуясь теоремой 3.3.1.2, мы восстанавливаем его до дерева изоморфного «нулевому».

2. Если дерево имеет m ярусов, где n

3. , получается, что «нулевое» дерево состоит из m ярусов Ї противоречие.

§3.3.2 Исследование высоты деревьев

Теорема 3.3.2.1

Если длина последовательности равна 2^k-1, то высота деревьев будет равна 2^k-1.

Доказательство:

Пример для k=1 и k=2 строятся довольно просто:

k=1 k=2

0 (1) 0 0 (1,0,0) 0

0 (0) 0 0 (0,1,0) 0

0 (1,0,1) 0

0 (0,0,0) 0

Докажем по индукции

1. База индукции:

Пусть k=3, тогда:

0 (1,0,0,0,0,0,0) 0

0 (0,1,0,0,0,0,0) 0

0 (1,0,1,0,0,0,0) 0

0 (0,0,0,1,0,0,0) 0

0 (0,0,1,0,1,0,0) 0

0 (0,1,0,0,0,1,0) 0

0 (1,0,1,0,1,0,1) 0

0 (0,0,0,0,0,0,0) 0

Высота дерева равна 2^k=7.

1. Пусть утверждение верно для n=k, тогда докажем его для n=k+1:

;

тогда:

Так как -й элемент равен «0» и остальные элементы симметричны относительно его, то в каждом последующем поколении этот элемент будет равен «0», следовательно, правая и левая части перейдут в состояние (0,0,…,0) через 2^k поколений. Таким образом, высота дерева будет 2^k +2^k-1=2^k+1-1=2ⁿ-1 ч.т.д.

Теорема 3.3.2.2

Если длину последовательности представить в виде

где , тогда 2^k-1 Ї высота «нулевого» дерева.

Доказательство:

По теореме 3.3.2.1 , где

с корнем

.

Возьмем последовательность длиной

;

заметим, что тогда:

(в связи с симметрией относительно )

Но тогда:

Высота дерева при n=2^n-1 равна высоте дерева при n=32^n-1. В связи с симметрией относительно

, мы получаем:

Высота дерева при n=2ⁿ⁺¹+2^n-1-1 равна высоте дерева при n=32^n-1-1.

Таким образом, мы получаем, что если представить длины последовательности в виде: , то 2-1^k Ї высота дерева.

Теорема доказана.

§3.4 Структура G при p2

Введение

В параграфе 2 мы рассматривали структуру графа состояний для произвольного линейного оператора над Z_p. В данном параграфе пойдет речь о структуре графа G определенного в параграфе 3.1. По аналогии со случаем p=2, по состоянию числовой полоски длины n (т.е. самого автомата с состояниями 0,1,..p-1) будем определять вектор , и рассматривать такое, что:

Все остальные основные определения вводятся аналогичным образом, как и в случае p=2, основным предметом исследования является структура графа G.

Одним из важных свойств оператора является его аддитивность:

которая следует из линейности оператора .

В предыдущем параграфе было доказано утверждение о том, что для произвольного линейного оператора «нулевое» дерево – p-нарное дерево с точностью до петли в корне (0,0..,0) (теорема 2.2). В данном параграфе будет определена высота нулевого дерева, тем самым будут определена высота дерева притягиваемого каждой точкой каждого цикла графа G (теорема 2.3).

Теорема 3.4.0

Вершина является висячей тогда и только тогда, когда n – нечётное и выполняется условие:

Доказательство:

Пусть у нас есть последовательности и

Тогда Но тогда .

Но по условию , т.е. для того чтобы вершина была висячей необходимо и достаточно, чтобы , т.е.

Теорема полностью доказана.

Теорема 3.4.1

Если длина последовательности кратна двум, то граф G_φ ― дизъюнктное объединение циклов.

Доказательство:

Воспользуемся тем, что дерево, притягиваемое каждой точкой каждого цикла, изоморфно нулевому дереву. Рассмотрим нулевое дерево. Его высота при n=2k равна нулю. Это следует из того, что , но m=2s+1, противоречие. Теорема полностью доказана.

Теорема 3.4.2

Если длину последовательности представить в виде p^k(2l)-1, (p,l)=1, тогда p^k есть высота «нулевого» дерева.

Доказательство:

Для начала докажем следующие леммы.

Лемма 1

– висячая вершина причем, .

Рис. 3.4.1 Пример для p = 5.

Доказательство леммы 1:

Для начала рассмотрим шахматную раскраску таблицы (2p^k-1)(p^k+1), строки которой есть последовательности , , …, (см. рис.). Тогда числа, стоящие на закрашенных позициях равны 0.

Остальные координаты образуют треугольник Паскаля с вершиной в 1 (см. пример на рис. 3.4.1 для p = 5). Тогда т.к. , то:

,

при этом (все значения биноминальных коэффициентов берутся по модулю p, так как мы рассматриваем вектор в пространстве )

Замечание:

Здесь и ниже, все многочлены рассматриваются над полем

Докажем, что

Действительно, т.к. (т.к. ), то: .

Откуда , ч.т.д.

Замечание

Висячесть вершины следует из теоремы 3.4.0

Следствие

– висячая вершина причем, .

Для доказательства домножим элементы рассмотренного выше треугольник Паскаля на i и в силу простоты p получим требуемое.

Лемма 2

Вершина н вида:

является висячей при условии, что число последовательностей вида , где не кратно p, причем .

Доказательство леммы 2:

Из теоремы 3.4.0, вершина является висячей при n нечётном и выполнении условия:

.

Таким образом, при подстановке соответствующих значений получим:

.

, где .

Таким образом, вершина вида:

является висячей при условии, что число конструкций вида , где m=1 либо (p-1), не кратно p. Вторая часть леммы следует из следствия леммы 1, причем, как и в лемме 1, Лемма доказана.

Приступим теперь к доказательству основной теоремы. Из леммы 1 следует, что высота дерева при равна p^k, из леммы 2 следует, что если высота дерева при равна высоте дерева при и, при условии, что (l,p)=1.

Теорема полностью доказана.

§4 Структура графа состояний оператора взятия разностей

Введение

В данном параграфе рассматривается структура графа состояний G оператора взятия разностей (см. [1]), который определяется следующим образом:

В ([1]) был рассмотрен только над Z₂, в этом параграфе оператор взятия разностей будет рассмотрен над полем Z_p. Оператор взятия разностей используется для анализа сложности функций (см. [1]).

На основе результатов параграфа 2 (теоремы 2.2, 2.3), для анализа структуры графа состояний оператора достаточно определить высоту нулевого дерева, тем самым будут определена высота дерева притягиваемого каждой точкой каждого цикла графа G (теорема 2.3).

Теорема 4.1

Если , то наименьший период функции (mod p) по i равен p^k.

Доказательство

Проверим сначала, что число p^k является периодом при :

Действительно, т.к.:

,

то , ч.т.д.

Теперь покажем, что это наименьший период, если , наименьший период должен быть делителем числа p^k, поэтому мы проверим, что p^k-1 – не период.

Докажем, что при число сочетаний , действительно, пусть j= i-(p-1)p^k-1, тогда . Тогда, т.к.:

,

откуда т.к. и , то ,т.е. , ч.т.д.

С другой стороны , поэтому число p^k-1 не является периодом функции

(mod p) по переменной i, когда , при этом условии .

Теорема 4.2

Если длину последовательности представить в виде: где , , тогда p^k есть высота «нулевого» дерева.

Доказательство

Проведем явное интегрирование функции периода n, т.е. определим , такое, что () = (1,1,…,1) (строгое определение интегрирования см. в [1])

Рис. 4.1

Легко видеть, что все интегрированные «интегралы» (с начальным условием при t=1) – это приведенные по модулю p косые линии треугольника Паскаля, на которых j = 0 для исходной функции , а затем, по мере повторного «интегрирования», ответы доставляют косые линии с j = 0,1,2… (см рис. 4.1)

Следовательно, для выяснения того, сколько раз удастся «проинтегрировать» функцию (т.е. определить высоту нулевого дерева) в классе n-периодических функций (т.е. в классе n-периодических последовательностей) остается выяснить, при каких значениях j функция аргумента i будет иметь период n.

В силу теоремы 4.1, если n= , то построение «нулевого» дерева, описанного выше, будет успешным до тех пор, пока «j-кратные интегралы» от функции будут оставаться n-периодическими функциями аргумента i. Но наименьший период указанной функции переменной i равен p^r при . Чтобы эта функция была n-периодической, необходимо, чтобы число n= делилось на наименьший период, т.е. чтобы . Откуда следует, что если длину последовательности представить в виде: n= , тогда p^k есть высота «нулевого» дерева, ч.т.д.

§5 Перспективы исследования

1. Более подробно исследовать структуру , а именно:

• Определить количество циклов и их длину;

• Описать множество корней деревьев и т.д.

1. Рассмотреть двумерный вариант клеточного автомата (на клеточном прямоугольнике ) с теми же вопросами, т.е. описать структуру графа состояний.

2. Более подробно рассмотреть матричную интерпретацию.

3. В связи с использованием одномерных клеточных автоматов, а также линейных операторов, в теории кодирования, найти количественные и качественные характеристики автомата (например, определить коллизии и т.д.).

4. В связи с тем, что некоторые правила «эквивалентны», изучить их относительно данного аспекта (т.е. найти некоторую «совместимость» между правилами). Определить условия эквивалентности правил, найти разбитие на классы эквивалентности. Данная задача является открытой проблемой.

§6 Резюме

Основным предметом исследования являлась рассмотрение структуры графа , более подробное изучение которой, является одним из наиболее перспективных направлений дальнейшего исследования. В общем случае получена следующая характеристика структуры графа :

1. Каждая компонента связности графа

является циклом (возможно длины 1), каждая вершина которого притягивает дерево (возможно нулевой высоты).

2. и ;

3. ;

4. «Нулевое» дерево ― p-нарное дерево с точностью до петли в корне e_n (0,0..0), причем его высота равна

• (для оператора , описывающего функционирование ACS-автомата и ), если длину последовательности представить в виде

• где , ;

• (для оператора , описывающего функционирование ACS-автомата и ) если длину последовательности представить в виде:

• где , .

5. «Нулевое» дерево ― p-нарное дерево с точностью до петли в корне e_n (0,0..0), причем его высота равна (для оператора взятия разности), если длину последовательности представить в виде:

где , ;

6. Все деревья (в том числе притягиваемые каждой вершиной каждого цикла) будут иметь столько ярусов, сколько и «нулевое», причем будут иметь такую же структуру. Т.е. дерево, притягиваемое каждой точкой каждого цикла графа состояний, изоморфно дереву, притягиваемому точкой e_n (0,0..0).

Используемые источники. Список использованной литературы

Используемые источники

1. М.С. Глущенко, П.С. Пересторонин, Почти центральная симметрия (доклад на IV Балтийском научно–инженерном конкурсе, Санкт-Петербург, 2008 г.)

2. М.С. Глущенко, П.С. Пересторонин, Почти центральная симметрия (доклад на XII Белорусской республиканской конференции учащихся общеобразовательных учреждений, Минск, 2008 г.)

Список использованной литературы

1. В.И. Арнольд, Сложность конечных последовательностей нулей и единиц и геометрия конечных функциональных пространств (из доклада Московскому математическому Обществу 22 ноября 2005 г.)

2. В.И. Арнольд, Топология и статистика арифметических и алгебраических формул, Успехи математических наук 58(2003), №4, 3-28

39

Характеристики

Список файлов реферата