Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла (страница 2)

3-ий метод. Метод идеальной точки (Оптимум Парретто).

4-ый метод. Метод мозговой атаки (коллективного распознавания).

4. Метод базовой точки в экономических системах.

К настоящему времени численные методы (приближенные методы) применяются тогда, когда переменных или критериев много.

В IXX столетии фр. Физик Ле Шателье открыл следующий принцип:

Е

Рис 1

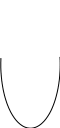
А

Рис 2

Б

сли система находится в состоянии устойчивого равновесия, то под действием внешних сил она может быть выведена из этого состояния, но так что будет обладать минимумом энтропии энергии. Это значит (см. рис.1), что если система находится в положении А, то по направлениям 1 и 2 ее бесполезно выводить из состояния устойчивого равновесия.

Е сли же система находится в положении Б, то, при выведении ее по направлениям 1 и 2 (см. рис.2) система не вернется.

Лауреат нобелевской премии, Пригожин И., в 1989 году, используя принцип Ле Шателье, о том что всякая система непременно возвращается в зону устойчивого равновесия, открыл новый метод в экономике – метод базовой точки:

Пусть состояние экономического процесса зависит от ряда параметров. Целевая функция имеет следующий вид:

х

X A E

–набор свободных параметров x₁,x₂,… x_n, которые надо оптимизировать.

a₁,a₂,… a_p – набор технических параметров, влияющих также на поведение целевой функции.

e₁,e₂,… e_m – набор стоимостных характеристик процесса, влияющих на поведение функции. Данная система широко применяется в настоящее время. Например, хорошо всем известная система налогообложения.

Множественная регрессия. Коэффициент эластичности.

Как правило, парной регрессией не обойтись, когда имеется группа взаимосвязанных признаков. Например, в модели участвуют след. хар-ки:

x1 – трудовые ресурсы, L

x2 – стоимость основных фондов, k

x3 – время, Т

x4 – зар. плата

x5 – средний возраст рабочего, и т.д.

Аналогично парной строится и множественная регрессия.

Сначала рассмотрим случай, когда один результативный признак у и фактор признак х₁, х₂,… х_n.

Различают аддиктивную (суммарную) линейную множественную регрессию вида

И мультипликативную (в форме произведения)

Параметры модели есть т.н. эластичности модели. Они показывают на сколько %-ов изм. рез-т у при изменении на 1% фактор признака х_i.

5. Идеальная матрица сравнений. Шкала сравнений.

При анализе интересующей нас структуры экономического объекта очень часто приходится принимать точные решения. Например, на поведение рыночной устойчивости предприятия (обеспечение максимального выпуска, связанного с ним дохода, в условиях инфляции, падения импорта, падения экспортных цен), нужно точно знать, сколько распределить средств, с учетом основных факторов производства на каждый из видов деятельности, зная цели.

Схема задачи следующая:

Объем средств

Производственный

сектор

Транспорт

Социально-бытовые службы

Существует универсальный метод, позволяющий точно сосредоточить денежные средства с учетом указанных целей (основоположник метода Т. Саати).

Идеальная матрица сравнений представляет собой квадратическую матрицу, построенную на сравнении ее элементов. Например, если один элемент, входящий в экономическую систему имеет одинаковую значимость с другим элементом, то в соответствующей паре этих элементов участвует число 1. Например, при приобретении материалов для крыши необходимы доски, шифер, гвозди и т.д. – часть элементов одинаковы по полезности. Если один элемент А, важнее элемента B, то пару (АB) в матрицу заносим 2 или 3.

(AB) B

|

|

A----(3)

А в пару BA заносим 1/2 или 1/3

(BA) (1/2, 1/3)

Если элемент А явно важнее чем элемент B, то в пару (A,B) заносим 4 или 5, в пару (B,A)=1/4, 1/5. Если элемент А значительно важнее, то 6 или 7, а (B,A)=1/6, 1/7. Если элемент А абсолютно важнее, чем элемент B, то заносим в пару (А,B)=8,9, а в (B,A)=1/8, 1/9.

Предположим, что, сравнивая объекты в экономической системе S мы вынуждены написать следующую таблицу сравнения.

Видим, что симметрично диагональные элементы взаимообратные по величине.

Для каждой матрицы характерны 2 основных компонента:

1. max собственное значение;

2. индекс согласованности, позволяющий судить о качестве построенной нами модели.

Характеристики

Список файлов реферата