151060 (732897)

Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

Фазові рівноваги та діаграми стану

Правило фаз.

Існування даної фази в системі або рівновага фаз можливі лише у визначених умовах, при зміні цих умов рівновага системи порушується, відбувається зрушення фаз або перехід речовини з однієї фази в іншу.

Можливість існування даної фази в рівновазі з іншими визначається правилом фаз або законом рівноваги фаз.

Умови, при яких система знаходиться в рівновазі, можуть змінюватися (система може знаходитися при різних температурах, тисках і концентраціях). Умовимося називати складовою частиною системи, або компонентом, кожну з хімічно однорідних речовин, які знаходяться в ній, або виділяються з неї і можуть існувати в ізольованому виді тривалий година. Компоненти системи, найменше число яких достатнє для утворення усіх фаз даної системи, називають незалежними компонентами.

Правило фаз у загальному виді виражається рівнянням

С + Ф= k + п

де С - число ступенів свободи або мінімальне число факторів, які можна змінювати незалежно один від одного без порушення рівноваги даної системи;

Ф—число фаз системи;

k - число незалежних компонентів системи;

п– число зовнішніх факторів, що впливають на положення рівноваги у даній системі.

Правило фаз формулюється так: сума числа ступенів свободи системи і числа фаз дорівнює сумі числа незалежних компонентів і числа зовнішніх факторів, що впливають на рівновагу цієї системи.

У залежності від числа ступенів свободи, системи можуть бути: безкомпонентними (при С=0), однокомпонентними (С=1), двох-компонентними (С=2) і різноманітними (С>2).

Однокомпонентні системи.

Якщо система складається тільки з одного компонента, тобто являє собою чисту індивідуальну речовину, те можливість одночасного існування всіх трьох фаз - твердої, рідкої і газоподібної, за правилом фаз визначається відсутністю ступенів свободи, тому що в цьому випадку:

С=1-3+2=0

і система безваріантна. Така система може існувати тільки при строго визначених значеннях температури і тиску (для води t=0,0075°С и р=4,579 мм рт. ст.). Зміна шкірного з цих розумів приводити до зникнення однієї з фаз і система стає двохфазною.

Найбільш цікавої однокомпонентною системою є двофазна система-рідина і насичена пари. У цьому випадку:

С=1-2+2=1

і система є одноваріантною. Отже, не порушуючи фазової рівноваги, можна довільно змінювати або температуру або тиск.

У таких системах строго однозначна залежність між температурою і тиском насиченої парі. Тому при зміні температури парі одночасно буде відповідно змінюватися тиск і, навпаки, при зміні тиску відповідно міняється і температура; для кожної рідини можна, таким чином, побудувати криву тиску насиченої парі. Як приклад приводитися крива тиску водяної парі (мал.1).

Для проведення дифузійних процесів необхідно знати залежність від температури тиску пари чистих рідин, що входять до складу сумішей. Звичайно такі криві будують на підставі дослідних даних, що для багатьох рідин приведені в літературі. Однак нерідко доводиться обчислювати тиск парів чистих рідин по теоретичних залежностях або непрямих методах.

При будь-якому рівноважному переході речовини з однієї фази в іншу дотримується залежність, що виражається рівнянням Клаузіуса — Клапейрона

де r — теплота фазового переходe (випаровування, плавлення, сублімації і ін.) у ккал/кг·мол;

— тепловий еквівалент роботи в ккал/кгс;

Т — абсолютна температура фазового переходу в °К;

Р — тиск у кгс/м²;

— зміна мольного об’єму речовини при фазовому переході в м³/кг·мол.

Рис.1. Крива тиску насиченої водяної пари.

Стосовно до двохфазної системи рідина — пара перепишемо це рівняння так:

де r – теплота випаровування при даній температурі в ккал1кг·мол;

V_п — молярний об’єм пари в м³/кг·мол;

V_ж — молярний об’єм рідини в м^а/кг-мол.

В області невисоких тисків пари молярний об’єм рідини дуже малий у порівнянні з молярним об’ємом пари, тому без великої похибки можна величиною V_ж знехтувати, приймаючи V_ж=0. Тоді

де R=1,99 ккал/кг·мол·°К.

При цих умовах рівняння приймає наступний вид:

або

або

При невеликих інтервалах температур величина r має приблизно постійне значення. Тоді інтегрування рівняння дає

де C – стала інтегрування.

По цьому рівнянню зручно вести практичні розрахунки, тому що воно є рівнянням прямої залежності логарифма тиску від зворотньої величини абсолютної температури. Якщо для якої-небудь однієї температури Т відомий тиск Р, то, знаючи величину r, можна з знайти числове значення константи C, після чого побудувати пряму в координатах lgP, і по ній знаходити значення Р для будь-яких інших температур.

Якщо величина r також невідома, те для побудови діаграми необхідно знати тиски при двох температурах, скласти два рівняння і, вирішуючи їх, визначити значення r і С.

Рівняння можна інтегрувати в межах від T₁ до Т₂ і відповідно від Р₁ до Р_2, тоді одержимо нове рівняння для визначення тиску насичених парів в залежності від температури:

Виходячи з умови прямолінійності функції, можна побудувати діаграму, що зв'язує тиск пари будь-якої речовини з тиском пари деякої стандартної речовини.

Відкладемо по осі ординат (рис.2) температуру кипіння стандартної речовини (води), а по осі абсцис - температуру кипіння різних речовин, при яких тиск їхньої пари такий ж, як і пари стандартної речовини. Лінії постійного тиску, що з'єднують температури кипіння даних речовин, що відповідають температурі кипіння стандартної речовини при тому ж тиску, зображуються на діаграмі у вигляді прямих. Так, наприклад, пари аніліну при 80° мають такий же тиск, як і пари води при 20°, і якщо останнє відомо, то може бути визначений і тиск пари аніліну при 80°.

Для зручності користування діаграмою (рис.2) будується додатково діаграма залежності тиску водяної парі від температури (рис.3). По цій діаграмі знаходять, наприклад, що при 20° тиск пари води дорівнює 18 мм рт. ст.; це і буде тиском пари аніліну при 80°. Так як пряма може бути побудована по двох точках, то для нанесення на діаграму лінії температур кипіння даної речовини необхідно знати принаймні дві температури кипіння при двох відповідних тисках. При цьому одною точкою може служити завжди відома температура кипіння речовин при 760 мм рт. ст., а другою будь-яка інша температура при будь-якому іншому тиску. Якщо друга температура невідома, то її можна визначити по рівнянню. Існує й інший, більш точний метод побудови кривої залежності тиску парі від температури. По осі ординат (шкала логарифмічна) відкладають тиски, а по осі абсцис — відповідні температури (рис.4); шкала осі абсцис нерівномірна, і її масштаб підібраний так, що залежність логарифма тиску деякої стандартної речовини (води) від температури виражається прямою лінією.

Після побудови лінії для води наносять лінії для парів інших речовин.

Переваги такої діаграми полягає в тому, що для близьких один до одного речовин того самого гомологічного ряду лінії температур кипіння сходяться в одній точці. Тому, якщо дана речовина належить до групи речовин, що мають загальну точку, то досить визначити експериментально лише одну точку (температуру кипіння при 760 мм рт. ст.), а другою служити загальна для всієї групи точка перетинання ліній.

Рис. 2. Діаграма для визначення тиску пари різних речовин у залежності від температури.

Двохкомпонентні системи.

Якщо система складається з двох або більшої кількості компонентів, то її стан і рівновага залежить не тільки від температури і тиску, але і від кількісного складу фаз.

Двохкомпонентна система, що складається з двох фаз, за правилом фаз має два ступені свободи;

С = k - Ф + 2 = 2 — 2+2 = 2

що означає, що в таких системах можна без порушення рівноваги фаз змінювати одночасно два фактори – температуру і тиск. Для характеристики рівноважного стану цих систем один з факторів приймають постійним, і тоді залежність між іншим фактором і складом фаз стає однозначною, тобто при постійному тиску кожній температурі, а при постійній температурі кожному тиску відповідають строго визначені склади фаз.

Температура, ⁰С

Тиск водяної пари, мм рт.ст.

Тиск водяної пари, мм рт.ст.

Температура, ⁰С

Рис.3. Діаграма залежності між тиском і температурою водяної пари.

Тиск , мм рт.ст.

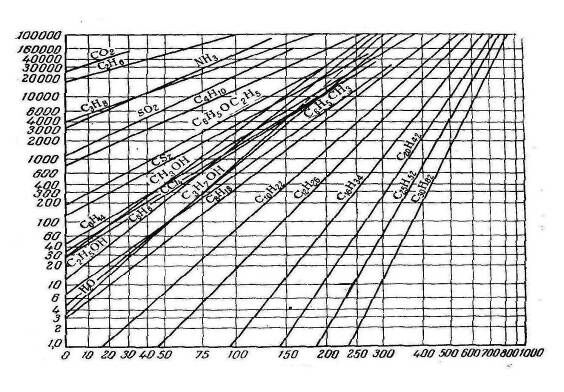
Температура, ⁰С

Рис.4. Діаграма залежності тиску пари різних речовин від температури.

8

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов реферата