part 2 (694717), страница 2
Текст из файла (страница 2)
регистре хранится число, наиболее точно аппроксимирующее сигнал, хранящийся на емкости ./. Этот двоичный код и пересылается в ЭВМ, после чего переходим к измерению следующего отсчета сигнала, поступающего на емкость с выхода фильтра / в момент подключения его к запоминающему конденсатору 2. Такой способ ана-лого-цифрового преобразования называют поразрядным взвешиванием.
Отметим, что большие перспективы в использовании универсальных аналого-цифровых преобразователей открываются в связи с мультипроцессорной реализацией различных методов цифровой обработки сигналов — дискретного преобразования Фурье, линейного предсказания, цифровой фильтрации и др. Для исследовательских целей этот тип ввода речевых сигналов в ЭВМ наиболее применим и в настоящее время, так как он достаточно гибок и позволяет сохранять все частотные составляющие речевых сигналов. Применяют аналого-цифровые преобразователи и в тех случаях, когда необходимо использовать фильтры с такими характеристиками, которые трудно реализовать на реальных физических элементах, а также в случаях, когда требуется частое изменение параметров фильтра, используемого при анализе сигнала, или подбор характеристик фильтра и когда реальный масштаб времени анализа не обязателен. Кроме того, ввод с аналого-цифрового преобразователя может оказаться целесообразным (и единственно возможным), когда ставится задача поиска информативных речевых параметров (не обязательно чисто спектральных) на значительном статистическом материале, собираемом в архиве речевых произнесений в цифровой форме.
Ввод сигнала с гребенки аналоговых фильтров. Второй тип ввода речевых сигналов в ЭВМ — это ввод сигналов с гребенки аналоговых полосовых фильтров, перекрывающих частотный диапазон речи, прошедшей через технические устройства (микрофон—микрофонный усилитель— (возможно) канал передачи). Информация с гребенки фильтров о медленно меняющихся огибающих сигнала с каждого фильтра поступает на электронный коммутатор (переключатель), который обеспечивает последовательное подключение напряжения с выхода каждого фильтра к аналого-цифровому преобра-
71
зователю. Коды с аналого-цифрового преобразователя (информация на выходе гребенки) с более низкой, чем при первом типе скоростью ввода, определяемой частотой опроса гребенки (частотой квантования), поступают в ЭВМ (рис. 2.2).
Достоинство этого способа заключается в том, что в памяти ЭВМ после ввода сигнала находится уже непосредственно динамическая спектрограмма речевого сигнала (картина «видимой речи»), и нет необходимости тратить машинное время на цифровое моделирование фильтров. Современные практические системы автоматического распознавания речи широко используют этот способ ввода информации о речевом сигнале, позволяющий автоматически анализировать полученные аналоговым способом медленно меняющиеся параметры тракта речеобразования.
72
. Этот тип устройств ввода речи обладает рядом недостатков. Что во-первых, то, что в них трудно изменить характеристики (Ьильтров (их средние частоты и полосы пропускания)—если они однажды вычислены и реализованы «в железе», то перейти к (Ьильтрам с другими характеристиками весьма непросто. Во-вторых, с гребёнки полосовых фильтров поступает много избыточной информации, что не только чрезмерно загружает память ЭВМ, но и приводит к тому, что программы надежного выделения основных параметров речеобразующего тракта, а также просодических параметров .достаточно сложны. Иногда формантные параметры мгновенную частоту основного тона, среднюю интенсивность (громкость) относят к наиболее информативным параметрам в отличие от параметров, представляющих просто энергию в полосах частот общего спектра сигнала. Гребёнка фильтров дает слишком много информации, так как энергия в полосах частот характеризует не только звуки речи, но и индивидуальные особенности речеобразующего тракта, эмоциональное состояние человека и т. д.
В связи с этим гребёнку фильтров используют, как правило, в дикторозависимых системах автоматического распознавания речи, работающих с предварительной настройкой на голос диктора и набор слов—рабочий словарь. Иногда такие системы называют адаптивными. В системах, работающих без предварительной настройки на голос конкретного диктора, которые иногда называют неадаптивными, используют гребенку для получения параметров следующего уровня распознавания речи, более независимых от дикторского произношения. Однако для систем автоматической диагностики заболеваний органов речеобразования, распознавания эмоционального состояния диктора и его индивидуальности использование гребёнки полосовых фильтров как первичного анализатора оказывается весьма эффективным. Для неадаптивных же систем автоматического' распознавания смысла сообщения, работающих от голоса произвольного диктора, полосовые фильтры, как правило, являются вспомогательными средствами первичного анализа.
Еще раз отметим, что алгоритмы автоматического распознавания смысла произнесенного только по картине видимой речи оказываются достаточно сложными. К тому же использование только
73.
гребенки фильтров не позволяет эффективно анализировать такие звуки речи, как глухие взрывные, длительность которых сравнима <: временем нарастания энергии на фильтре.
Ввод в ЭВМ информативных речевых параметров. Следствием развития системы ввода второго типа — системы анализа речевых сигналов, основанной на выделении аналоговыми средствами некоторых медленно меняющихся параметров речи и их последующей программной обработки, являются системы, использующие третий тип ввода сигналов в ЭВМ. В таких системах первичным анализатором речи служат устройства выделения информативных речевых параметров, близких к параметрам речеобразующего тракта. Ввод третьего типа позволяет еще сильнее сжать информацию о речевом сигнале, поступающую в ЭВМ.
Блок-схема одного из устройств выделения речевых признаков •представлена на рис. 2.3. Общая идеология таких устройств и обоснование выбранных признаков речевого сигнала разработаны в Вычислительном центре Академии наук СССР и Институте проблем
74
передачи информации Академии наук СССР. Усиленный речевой сигнал подается на 16 каналов, из которых 9 дают бинарный выход сигнализирующий о наличии или отсутствии соответствующего признака. Эти признаки названы групповыми, их комбинация может дать представление лишь о способе образования звуков, т. е. о принадлежности к группе звуков, сходных по способу образования — шумные, взрывные, гласные, но не о звуке в группе. Остальные 7 каналов дают количественные характеристики шумных звуков речи и гласных, т. е. позволяют классифицировать эти звуки по месту их образования. К признакам места образования шумных здесь относят:
— число переходов сигнала через нулевой уровень в положительном направлении No, т. е. общее число положительных импульсов клиппированного, или предельно ограниченного речевого сигнала, при котором он сохраняет лишь два возможных значения амплитуды (уровня);
— число положительных импульсов клиппированной речи, превышающих длительности в 100, 200 и 400 мкс;
— число положительных импульсов клиппированной речи, не превышающих 50 мкс.
К признакам места образования гласных причисляют значения первой и второй формантных частот. К групповым двоичным признакам, принимающим только два значения—О и 1, относятся:
признак наличия энергии сигнала, превышающей ранее заданный уровень (порог) в области низких частот (если пороговый уровень энергии не превзойден, считается, что данный групповой признак отсутствует); признак наличия энергии, превышающей пороговый уровень в области высоких частот; трехуровневый признак огибающей сигнала. Трехуровневый признак наличия участков с повышенным числом перехода сигнала через нулевой уровень характеризует усредненную мгновенную частоту сигнала. Кроме того, в число двоичных признаков входит признак повышенной частоты основного тона, определяющий «высокочастотные» женские и детские голоса.
.Признаки вводятся в машину каждые 10 мс в мультипрограммном режиме на фоне решения других задач. Трехпороговый признак плотности нулей представляет собой три одинаковых канала
75
Таблица 2.1
| Звук | —о | /о | Wl | N, | Ns | К. | л^в | N, | nh | /Л. | N.. |
| 21 | 3900 | 11 | 3 | 2 | 1 | 1 | — | — | — | — | |
| 24 | 3700 | 16 | 3 | 1 | — | — | — | 8 | |||
| 22 | 5400 | 15 | 2 | 1 | 1 | — | — | — | 14 | ||
| С | 24 | 4700 | 12 | 3 | 1 | 1 | — | — | — | — | 20 |
| 28 | 4900 | 8 | 4 | — | — | — | — | 16 | |||
| 29 | 4750 | 8 | 2 | — | — | — | 23 | ||||
| 36 | 1950 | 9 | 1 | 3 | 3 | 1 | — | — | — | 10 | |
| 40 | 850 | 3 | 4 | 2 | 2 | 3 | 1 | — | 1 | — | |
| 48 | 300 | 1 | ч 0 | ||||||||
| э | 50 | 550 | 1 | 2 | — | 1 | 2 | 1 | 1 | — | |
| 54 | 750 | 2 | — | 1 | 1 | — | 1 | 1 | 1 | — | |
| 60 | 600 | 1 | — | — | — | — | 5 | 2 | — | — | |
| 58 | 650 | 5 | — | — | — | — | 5 | 1 | — | — | |
| 57 | 500 | 2 | — | .— | — | 5 | — | — | — | ||
| 57 | 600 | 2 | 1 | 2 | — | 1 | — | 1 | — | — | |
| 42 | 650 | 1 | 5 | 1 | 1 | 1 | — | 1 | — | — | |
| 36 | 350 | 2 | 2 | 1 | — | — | |||||
| 33 | 250 | . | 1 | — | — | 2 | — | ||||
| м | 26 | 250 | —— | — | —— | — | — | — | 1 | 2 | — |
| 23 | 200 | — | — | — | — | 1 | 1 | — | |||
| 22 | 250 | „ | 1 | — | — | — | 2 | — | |||
| 20 | 200 | 1 | 1 | ||||||||
с порогами на частоте в 200, 3500 и 5000 Гц, что позволяет уже на уровне аппаратуры класс шумных звуков разделить на высоко-и низкочастотные. Аналогичным образом построен трехпороговый признак огибающей. Отметим, что аналоговые устройства выделения информативных речевых признаков могут дополняться другими каналами, видоизменять общую структуру, включать в свой состав устройства ввода второго типа (гребёнки полосовых фильтров).
76
2.2. ВЫЧИСЛЕНИЕ ПРИЗНАКОВ ПЕРВИЧНОГО ОПИСАНИЯ РЕЧИ ЦИФРОВЫМИ МЕТОДАМИ
При анализе речи цифровыми методами в ЭВМ с аналого-дифрового преобразователя поступают дискретные отсчеты речевого сигнала, т. е. речь представляется .набором чисел. Последовательность этих чисел подвергается программной обработке по определенным алгоритмам цифровой обработки сигналов для того, чтобы представлять речь в более простом виде—меньшим набором чисел, первичными признаками (признаками первичного описания), которые дают достаточно полное описание речевого сигнала. Признаки (параметры) первичного описания программно вычисляются за время, в течение которого положение речеобразующих (артикуля-торных) органов почти не меняется,—за 0,01—0,02 с (10—20 мс). На отрезках такой длительности аналого-цифровой преобразователь, «оцифровывающий» речевой сигнал с частотой 20 кГц, дает 200— 400 отсчетов. Признаков же первичного описания на отрезках такой длительности обычно 10—20, а иногда и меньше, поэтому уменьшается объем памяти,, которая отводится в ЭВМ для -хранения речи, и увеличивается скорость последующей обработки сигнала.
Первичные признаки записываются в запоминающем устройстве в виде таблицы (матрицы) параметров. Каждая строчка такой таблицы—это набор признаков, вычисленных при цифровой обработке речи за 10—20 мс, а каждый столбец показывает изменение данного признака во времени (через 10—20 мс). Например, несложная табл. 2.1 соответствует параметрическому представлению слова «семь». При этом признаками первичного описания являются: средняя энергия сигнала Ац, средняя частота перехода сигнала через нуль /о (усредненная мгновенная частота) и числа положительных импульсов клиппированной речи. Иными словами, речи, представленной прямоугольными импульсами, полученными из первоначальной речевой волны после ее усиления и предельного ограничения по амплитуде, когда сигнал принимает лишь два значения, одному из которых может соответствовать 0, а другому 1. Положительные импульсы находятся в диапазоне длительностей 100—200
77
(Л';), 200—300 (ЛЛ;), 300—400 (Л^з), 400—600 (Л^), 600—800 (/Vg), 800—1200 (Ns), 1200—1800 мкс (Na), свыше 1800 мкс (Nis) и ме. нее 50 мкс {Ns). Все признаки измерены на интервалах в 20 мс.
Данные для такой таблицы получаются цифровыми методами с помощью очень простых алгоритмов. Средняя интенсивность сигнала Ay на отрезке в 20 мс может быть получена сложением 400 отсчетов входного сигнала, поступающих с аналого-цифрового преобразователя, без учета их знака и с последующим делением на 400. Усредненная за время анализа «мгновенная» частота сигнала Го вычисляется подсчетом точек, где соседние значения отсчетов имеют разные знаки. Число точек, в которых сигнал меняет знак, деленное пополам, определяет среднее число переходов сигнала через нуль в положительном направлении. Если среднее число умножить на 100, то получится усредненная мгновенная частота fo. Таким образом, простейшей формулой, определяющей алгоритм вычисления усредненной мгновенной частоты сигнала, является формула
где Ai и Лц.1—соседние отсчеты речевого сигнала; sign—произведение двух чисел Л, и Лг+i, равное 1, если одно из чисел (неважно какое) положительное, а другое — отрицательное.
Числа положительных импульсов клиппированной речи, определяющих интервалы между нулями в возможных интервалах длительностей (Ni—A^ia), также вычисляются очень просто. Представьте себе, что в массиве чисел, которые соответствуют речевому сигналу и получаются с помощью аналого-цифрового преобразователя, отмечены места, где сигнал меняет знак с отрицательного на положительный, и наоборот. Числа, представляющие речь, идут, например, так: 18, 13, 10, 7,3, —1, —8, —12, —20, —32, —25, —19,
—13, —6, —2, 4, 12, 16, 29, 21, 25, 14, 17, 12, 6, —2. —5, —11,
—18, —29, —29, —31, —21, —13 и т. д. В этой последовательности соседние числа трижды имеют разные знаки. Дважды сигнал переходит из области положительных значений в область отрица-
—ro-T^iii-.v г, r>ni»u пяэ—ия области отоицательных в область положи-
тельных (эти числа в массиве подчеркнуты). Если частота квантования аналого-цифрового преобразователя 20 кГц, то временные отрезки, которым соответствует интервал между двумя соседними яисламп — 50 мкс (за одну секунду в память ЭВМ вводится 20 тысяч отсчетов речевого сигнала). Значит, достаточно подсчитать, сколько чисел прошло между сменой знака с отрицательного на положительный, и наоборот, чтобы определить длительность одного положительного прямоугольного импульса клиппированной речевой волны. В нашем случае число интервалов между второй и третьей сменами знаков составляет 12, т. е. длительность прямоугольного импульса 12Х50—600 мкс. Можно полагать, что параметр Ms должен увеличиваться на единицу. Для каждого из параметров ^V,—,Vi6 имеются ячейки-счетчики, которые называются счетчиками селекции импульсов по длительности и куда программа за время анализа (10—20 мс) заносит для суммирования единицы, если выполнено условие записи в соответствующую ячейку памяти после проверки длительности положительного импульса. Это делается сравнением длительности импульсов с константами, определяющими, в какой из диапазонов длительностей попало данное число.
Что дает такая таблица признаков? Рассмотрим данные табл. 2.1 более внимательно. В ней даются 22 строки. Это означает, что длительность слова «семь» 440 мс, так как каждая строка таблицы характеризует отрезок сигнала длительностью в 20 мс. Столбцы таблицы показывают, как изменяются признаки на протяжении слова. Слово начинается с фонемы, характеризующейся высокой мгновенной частотой: 4—5 кГц. Далее следует участок, на котором самая высокая громкость и мгновенная частота снижается до 600— 700 Гц. Затем следует конечный участок слова, на котором и интенсивность падает, и усредненная мгновенная частота снижается до 200—250 Гц. Это соответствует последовательности звуков с—э—м. Особенно следует сказать о признаках Ni—A^g. Для щелевого с длительности положительных импульсов фактически лежат в пределах До 200 мкс. Для ударного гласного э эти длительности лежат в диапазоне 300—800 мкс, а для носового м—в пределах 1000 мкс и более.
79
Рассматривают цифровой анализ сигналов во временной и спектральной областях. В первом случае признаки более компактного представления речи получаются непосредственно из оцифрованного речевого сигнала, так, как в рассматриваемом примере. Во втором — параметры извлекаются на основании анализа динамической спектрогрммы, которая характеризует изменяющийся во времени спектр звуков речи. Спектральный анализ (получение динамической спектрограммы) на ЭВМ осуществляют с помощью алгоритма дискретного преобразования Фурье, который кратко будет рассмотрен далее,
Отметим, что к методам анализа речевых сигналов во временной области относится автокорреляционный анализ. Это метод обработки сигналов, основанный на временнной задержке начального сигнала с последующим умножением задержанного сигнала на исходный. Автокорреляционная функция — это функция времени, показывающая, как зависят последующие значения речевого сигнала от предыдущих: чем больше ее значение, тем большая зависимость определения последующего отсчета сигнала от предыдущего, т. е. последующие отсчеты более коррелированы с предыдущими. На звонких участках речи автокорреляционная функция квазипериодична, на глухих, где речевой сигнал представляет собой фрикативный квазислучайный шум, автокорреляционная функция непернодична, случайна. На этом основано выделение по автокорреляционной функции участков, соответствующих глухим и звонким звукам речи, а также определение периода основного тона. На рис. 1.14, г представлена автокорреляционная функция для звонкого участка речевого сигнала. С помощью автокорреляционной функции можно определить некоторые важные свойства речевого сигнала, в частности, узнать, является ли даяный сигнал периодическим, т. е. присутствует ли в нем основной тон. Автокорреляционная функция для дискретной последовательности х(п) вычисляется по формуле
R(s)=-Zx(n)x(n—s), s=0, I, 2, ..., N, n=s
где х(п)—отсчет речевого сигнала в п-й момент времени; п=0, 1, 2, ..., N; N+l—количество отсчетов в интервале анализа; .V-4-1— количество отсчетов автокорреляционной функции.
80
Автокорреляционная функция является четной функцией, т. е. R(s)==R(—s), и максимального значения достигает при s=0. Величина R(o) равна полной энергии речевого сигнала на интервале анализа, что весьма важно для определения энергии сигнала, если известно значение автокорреляционной функции R(o).
Вычисление отсчетов автокорреляционной функции можно производить в процессе ввода речи с аналого-цифрового преобразователя, уточняя с каждым вновь принятым отсчетом сигнала значение отсчетов автокорреляции по рекуррентной формуле
R»o»(s)=Rc-r!4?(s)+x(n)x(n—s), s==0, I, 2, ..., N.
В начале интервала анализа принимаем R(s)=0, s=0, I, 2,..., ..., N, а предыдущие отсчеты сигнала — равными нулю. Отметим, что в аналоговую аппаратуру выделения информативных признаков, описанную ранее, может быть включен канал, дающий возможность получить значения автокорреляционной функции на интервале анализа — коррелометр.
2.3. КРАТКИЕ СВЕДЕНИЯ О СПЕКТРАЛЬНОМ АНАЛИЗЕ РЕЧИ
Ранее упоминалось о том, что речевой сигнал можно рассматривать как реакцию системы с медленно меняющимися параметрами речеобразующего тракта на периодическое или шумовое возбуждающее колебание. Многообразие звуков речи определяется многообразием форм голосового тракта. При построении модели речевого сигнала, например в говорящих машинах — синтезаторах речи, принимают, что на относительно коротких временных интервалах (10—20 мс) формы голосового тракта при произнесении звуков речи существенно изменяться не могут. На таких коротких интервалах подобные формы тракта считают постоянными. А это означает, что электрический фильтр с резонансными свойствами, отражающими свойства голосового тракта, тоже можно рассматривать на коротких временных интервалах как систему с постоянными параметрами. Это позволяет моделировать сложный процесс ре-чеобразования электрической цепью или программно на ЭВМ.
6 Заказ № 901
81
Модель речевого сигнала для звонкого звука представлена на рис. 2.4. Импульсы возбуждения, т. с. электрические сигналы, эквивалентны толчкам воздуха на выходе голосовых связок (рис. 2.4, а); ^:o=2л/Гo—частота импульсов возбуждения, или частота основного тона. В спектральной области энергия таких импульсов представляется гребенчатым спектром (рис. 2.4,6). Это означает, что квазипериодический сигнал, соответствующий импульсам возбуждения, имеет частотные составляющие лишь на гармониках, кратных частоте основного тона на частотах Fo, 2Fo, 3F„ и т. д. (точнее, в областях вблизи этих гармоник).
Для аналоговых электрических сигналов выходное напряжение определяется операцией свертки функции возбуждения и отклика (реакции) фильтра на единичный скачок напряжения на его входе. Иногда свертку для аналоговых сигналов называют интегралом Дюамеля. Операцию свертки для аналоговых сигналов мы рассматривать здесь не будем из-за се относительной сложности. Попытаемся кратко описать, что такое операция свертки для случая дискретных сигналов.
Из теории фильтрации следует, что если возбуждающий сигнал, поступающий на фильтр, представлять последовательностью его
82
отсчетов, то сигнал на выходе фильтра, который моделирует голосовой тракт, можно представить операцией дискретной свертки, которая учитывает реакцию фильтра на входные (возбуждающие) сигналы. Дискретный сигнал на выходе фильтра вычисляется по сигналу на входе Е(п) и отклику (реакции) h(n) фильтра на единичный импульс 6(ri), равный единице в дискретные моменты времени п и нулю вне этих дискретных моментов. Дискретная свертка вычисляется
S(n)=^ E(k)h(n—k)=E(n)* h(n),
k=—oa
где символ * означает свертку. Вычисление этой громоздкой суммы произведений упрощается, если учесть, что большая часть этих произведений равна нулю из-за конечной длительности возбуждающего сигнала Е(п).
Итак, если S(n)—речевой сигнал на входе фильтра, моделирующего голосовой тракт, то значение каждого отсчета сигнала можно представить сверткой S(n)=E(n)s h(n).
Переход к анализу сигналов в спектральной области позволяет достаточно просто получить спектр выходного речевого сигнала, если известен спектр возбуждающего сигнала и передаточная функция фильтра, моделирующего голосовой тракт. Спектр выходного сигнала (звонкого звука речи), т. е. совокупность значений амплитуд всех частотных составляющих, образующих данный звук (рис. 2.4,6), можно получить, перемножив (а не произведя сложную операцию свертки) спектральные составляющие гребенчатого спектра сигнала возбуждения, которые берутся в точках, кратных частоте основного тона, на значения передаточной функции голосового тракта. На этом рисунке видны подъемы спектра на формант-ных частотах f[, /•2, Fs, Ft-
Разработаны математические методы (аппарат прямого и обратного преобразования Фурье), позволяющие осуществлять переход к представлению сигнала в спектральной области, если известна временная картина речевой волны. И наоборот, если известно спектральное представление речевого сигнала на последовательных отрезках речевой волны, то можно получить временную картину речи,
б* 83
т. е. увидеть ее осциллограмму и услышать звучание синтезированной речи, когда известны только амплитуды ее частотных составляющих.
Спектральное представление оцифрованного речевого сигнала основывается на кратковременном дискретном преобразовании Фу- i рье, учитывающем обстоятельство, о котором мы уже упоминали:
на относительно коротких временных интервалах (10—20 мс) свойства голосового тракта, а значит, и передаточная функция тракта, определяющая спектральные свойства речевого сигнала, существенно не изменяются. Хотя формула дискретного преобразования Фурье строго теоретически представляет бесконечное суммирование произведений дискретных отсчетов сигнала и синусоид, частоты которых изменяются дискретно от некоей начальной синусоиды до бесконечности, реальное (кратковременное) преобразование Фурье использует дополнительный сомножитель. Он называется весовым окном, или весовой функцией, которая имеет ненулевые значения лишь на окне (участке сигнала длительностью 10—20 мс), где мы принимаем постоянными, независимыми от времени частотные составляющие звука.
Формула кратковременного преобразования Фурье, которым пользуются при расчетах дискретных спектров звуков речи, имеет вид
Кратковременное преобразование Фурье позволяет представлять речь динамической спектрограммой, или временной последовательностью спектральных срезов, кратковременных спектров, каждый
84
из которых получен для окна, короткого отрезка речевого сигнала, на котором, как мы считаем, не изменяются спектральные свойства. Динамическая спектрограмма (картина «видимой речи», если ее выводят на печать в виде рисунка) представляет характеристики речи в координатах «время — частота — амплитуда». Алгоритм дискретного преобразования Фурье позволяет изобразить спектр значениями амплитуд частотных составляющих на равностоящих частогах. По спектральному описанию (кратковременному спектру) можно определить — и довольно несложными математическими методами — основные параметры речеобразующего тракта: частоту основного тона, формантные характеристики, энергии в полосах частот.
В настоящее время разработаны алгоритмы быстрого вычисления значений спектральных составляющих по дискретным отсчетам сигнала. Такие алгоритмы называются алгоритмами быстрого преобразования Фурье. В их основе лежит разбиение последовательности Л" отсчетов речевого сигнала на составные части (N берется всегда составным числом), для которых вычисления осуществляются значительно быстрее. Обычно N берется как 2й, т. е. берутся Л', равные 128, 256 или 512 (27, 28 или 29) в зависимости от частоты квантования сигнала и длительности окна анализа. Отметим, что разработаны также ускоренные методы для вычисления операции свертки.
2.4. НЕМНОГО О ЛИНЕЙНОМ ПРЕДСКАЗАНИИ
В последние годы приобрел широкое распространение метод анализа речевых сигналов во временной области, который получил название линейного предсказания или линейного прогноза. В развитие этого метода анализа речи большой вклад внесли советские ученые А. А. Харкевич, Н. Н. Акинфиев, А. Н. Собакин и др.
Линейное предсказание—это метод анализа, основанный на цифровой фильтрации оцифрованной речи, при которой текущий отсчет сигнала может быть «предсказан» (например, при автоматическом синтезе речи) линейной комбинацией прошлых значений выходной последовательности и настоящих, а также прошлых значе-
85
ний входной последовательности. Понятие «линейная комбинация» означает сумму произведений известных дискретных отсчетов сигнала (входных и выходных), умноженных на соответствующие коэффициенты линейного предсказания для предсказания (определения) неизвестного выходного отсчета. При линейном предсказании основная задача анализа речи — найти коэффициенты этой линейной комбинации, которые дают минимальную ошибку предсказания на участке анализа сигнала.
Модель сигнала, наиболее часто используемая при линейном предсказании, сводится к получению неизвестного отсчета х(п) без учета предыдущих входных воздействий на выходе некоторой системы
р
х(п)=^ dnx(n—k)+ Gu(n), k=i
где р — число коэффициентов, используемых в модели; йк — коэффициенты линейного предсказания; G—коэффициент усиления, определяющий вклад в линейную комбинацию входного отсчета;
и(п) — текущий входной отсчет.
Задача анализа оцифрованной речи сводится к определению коэффициентов Ок и G этой модели. Метод определения величин, используемых при расчетах, называется методом наименьших квадратов. Чтобы понять его суть, пойдем на некоторые упрощения в представлении текущего выходного отсчета. Будем считать, что входное воздействие на вход системы, моделирующей формирование речевых сигналов, ненаблюдаемо, что справедливо для ряда прикладных задач. Тогда на интервале анализа текущие отсчеты речевого сигнала приближенно опишутся линейной комбинацией предыдущих значений:
Коэффициенты линейного предсказания а„ вычисляются из условия минимума среднеквадратичного значения ошибки на интервале анализа. На этом интервале полная среднеквадратичная ошибка складывается для каждого отсчета сигнала, представленного линейной комбинацией р предыдущих значений сигнала
Здесь п — номер предыдущего отсчета сигнала на анализируемом интервале; k — номер предыдущего отсчета сигнала при построении линейной комбинации, представляющей текущий отсчет.
Коэффициенты линейного предсказания, минимизирующие полную ошибку предсказания Е, находятся после того, как выражение для полной ошибки продифференцировать по всем коэффициентам Он (полная ошибка предсказания может рассматриваться как функция параметров ак) и приравнять нулю все частные производные:
дЕ/дс>к=0'Л<1г<р.
Частными производными называются производные сложной функции по одной из переменных с учетом того, что остальные переменные при таком дифференцировании считаются константами.
Результатом дифференцирования по а,, является система из линейных уравнений с неизвестными коэффициентами линейного предсказания, минимизирующими ошибку линейного предсказания на отрезке анализа сигнала, где коэффициенты йк считаются постоянными. Решение этой системы линейных уравнений, а также другие вопросы, связанные с линейным предсказанием речи, подробно рассмотрены Маркелом и Грэем в книге «Линейное предсказание речи».
87
2.5. АНАЛИЗ КЛИППИРОВАННОЙ РЕЧИ
Клиппированным речевым сигналом называют предельно ограниченный «стриженый» сигнал, сохраняющий лишь два возможных значения, которые условно принимаются за +1 и —1
(рис. 2.5).
В различных работах отмечается, что, несмотря на недостаточную естественность звучания клиппированной речи, ее разборчивость оказывается достаточно высокой, причем разборчивость речи повышается, если до клиппирования речевой сигнал подвергнуть дифференцированию. Это явление означает, что информация о распределении интервалов между нулевыми пересечениями сигнала может быть использована для построения устройств автоматического распознавания и синтеза речи. Привлекательность автоматического анализа клиппированной речи и использования ее параметров для целей построения говорящих и понимающих речь машин лежит в простоте получения этих параметров.
Если речевой сигнал представлен дискретной последовательностью его отсчетов -J х(п)} , то фиксирование момента перехода сигнала через нуль происходит, когда знаки двух соседних дискретных отсчетов речевого сигнала различны, т. е.
sign[x(n)]-^s\gn[x(n—l)'\.
Информация об общем числе переходов сигнала на определенном интервале и различных диапазонах длительностей участков между нулями часто используется для грубой оценки частотного состава сигнала. Существует тесная связь между числом нулевых пересечений и распределением энергии по частотам. Общее число переходов сигнала через нуль, величину Л'о, вычисляемую для дискретной последовательности А" отсчетов, можно представить в виде
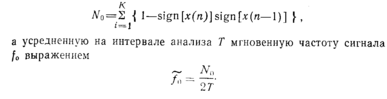
Существуют системы автоматического распознавания речи, в которых, как об этом говорилось ранее, нулевые пересечения используются для приближенного определения формантных частот. На рис. 2.6 показано, как оцениваются формантные частоты с помощью схемы анализа нулевых пересечений после прохождения сигнала через полосовые фильтры, которые перекрывают диапазоны частот, соответствующие формантным областям (первая форманта Fi лежит в диапазоне 200—900 Гц, вторая—550—2700 Гц и третья— 1100—2950Гц).
Иногда при распознавании речевых сигналов используют так называемую гребенку временной селекции, которая позволяет оценить ширину импульсов клиппированного сигнала и тем самым провести более точный анализ во временной области, что позволяет относительно простыми средствами отличать одни классы звуков от Других. Так, для фрикативных согласных селекторы импульсов по Длительности дают возможность отделить диффузные (звуки с ши-
89
Рис. 2,7. Блок-схема временной селекции интервалов между нулями
роким спектром типа ф) от компактных (спектр которых сосредоточен в относительно узкой области—с, ш).
Блок-схема селекции импульсов клиппированного речевого сигнала по длительности показана на рис. 2.7.
Обычно с учетом особенностей клиппированных согласных и гласных выбирают пороги временной селекции, равные 50, 100, 200, 400, 600 и 800 мкс (первый селектор отбирает узкие импульсы, длительность которых меньше 50 мкс). Поступающие для дальнейшего анализа числа (со счетчиков импульсов) позволяют получать распределение интервалов между нулями в диапазонах длительностей между пороговыми значениями селекторов — узлов, пропускающих на счетчики импульсы, превосходящие (или не превосходящие) по длительности заданный порог.
Следует отметить, что энергия и переходы сигнала через нуль часто совместно используются для разработки алгоритмов выделения моментов начала и конца речевой реализации (изолированного слова фразы). Такой алгоритм применен, например, в отечественной промышленной системе распознавания изолированных слов ИКАР.
90
Подобные алгоритмы основываются на тщательном исследовании статистических параметров функций среднего значения сигнала я числа нулевых пересечений для шумов различной природы и различных звуков фраз и изолированных слов.
2.6. ГОМОМОРФНАЯ ОБРАБОТКА СИГНАЛОВ
Как было показано ранее, речевой сигнал на коротких интервалах можно рассматривать как отклик системы с медленно меняющимися параметрами на периодическое или шумовое возбуждение. Это означает, что во временной области дискретный сигнал у(п) представляется результатом свертки функции возбуждения х(п) с импульсной реакцией голосового тракта h(n). Гомоморфная обработка речи сводится к решению обратной задачи — имея речевой сигнал у(п) =х(я)* h(n), можно получить параметры сигналов, участвующих в свертке. Эта задача называется иногда задачей обратной свертки или развертки.
Смысл гомоморфной системы анализа становится более понятным, если учесть, что в частотной области речевой сигнал представляется произведением спектра сигнала возбуждения и передаточной функции частотной характеристики голосового тракта, учитывающего спектральные свойства излучателя (произведением P(f)=E(f) F(f), см. рис. 1.3). Это означает, что в спектре речевого сигнала содержится информация о спектре сигнала возбуждения и передаточной функции голосового тракта. Гомоморфная обработка сигнала — это способ извлечь информацию об основном тоне и формантных частотах на основании преобразований сигнала, которые будут описаны далее.
Если произвести кратковременное дискретное преобразование Фурье (т. е. получить динамический спектр речевого сигнала), а затем прологарифмировать спектральные составляющие динамического спектра, то каждый спектральный отсчет можно рассматривать как сумму логарифмов спектра сигнала возбуждения и частотной характеристики речевого тракта (по свойству логарифмической функции логарифм произведения равен сумме логарифмов со-
91
преобразование Фурье
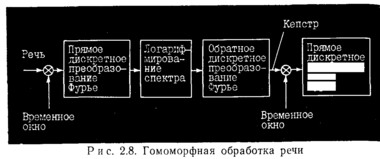
множителей). Обратное дискретное преобразование Фурье прологарифмированного спектра позволяет вновь перейти к анализу сигнала во временной области. Сигнал, полученный в результате обратного дискретного преобразования Фурье прологарифмированного спектра, называется кепстром входного сигнала, равного сумме кеп-стров сигналов возбуждения и составляющих, обусловленных особенностями речеобразующего тракта. В результате подобных преобразований дискретный речевой сигнал, представляющий собой свертку сигнала возбуждения и импульсного отклика фильтра, моделирующего голосовой тракт, приближенно преобразуется в сложение кепстров (рис. 2.8).
Логарифм кратковременного спектра вокализованных звуков содержит медленно меняющуюся составляющую, обусловленную передаточными свойствами голосового тракта, и быстро меняющуюся периодическую составляющую, которая вызывается периодическим сигналом возбуждения (рис. 2.9, а). Для невокализованной речи прологарифмированный спектр носит характер, показанный на рис. 2.9. б. Спектр содержит случайную составляющую с быстрыми изменениями.
Кепстры отрезков вокализованной и невокализованной речи (рис. 2.10) показывают, что медленно меняющаяся часть прологарифмированных значений кратковременного спектра представлена составляющими кепстра в области малых времен. Быстро меняющаяся периодическая составляющая прологарифмированного спек
92
р,.
тра, соответствующая частоте основного тона, в кепстре вокализованной речи проявляется в виде резкого пика, расположенного от начала координат на расстоянии, равном периоду основного тона. Кепстр невокализованной речи (рис. 2.10, б) таких пиков не имеет.
Если кепстр перемножить на подходящую функцию окна, например на прямоугольное окно, пропускающее только начальные участки кепстра (которые соответствуют области малых времен и отражают относительно медленно меняющиеся параметры голосового тракта), а затем вычислить дискретное преобразование Фурье результирующего взвешанного кепстра, то получим сглаженный спектр сигнала (см. рис. 2.8). Он отражает резонансные свойства тракта, позволяя оценивать частоты и полосы формант. Наличие или отсутствие ярко выраженного пика в области, соответствующей диапазону изменений периода основного тона, указывает на характер возбуждения, а местоположение пика является хорошим индикатором периода основного тона (рис. 2.10,0^).
РЗ



























