183541 (599256), страница 2
Текст из файла (страница 2)

Доказати однорідність першого степеня виробничої функції Кобба-Дугласа.
Для другої галузі необхідно розглянути лінійну виробничу функцію
2=b12+b2L2,
b1=10i, b2=і,
де і - номер заданого варіанту. Дослідити цю функцію, для цього обчислити характеристики




 ,
,  ,
,  ,
,  ,
,  .
.
Доказати однорідність першого степеня лінійної виробничої функції.
4.3 Дослідження моделі "витрати-випуск" Леонтьєва
В моделі Леонтьєва діють підсистема виробництва продукції F та блок розподілу RX, змінні X,Y,W (рис. 4.1).
Якщо позначити через Xi - валову продукцію і-ї галузі, Yi - кінцеву продукцію і-ї галузі, Wi – проміжну продукцію і-ї галузі, то можна записати,
Xi-Wi=Yі,  .
.
Тут n - кількість галузей. В цій моделі діє припущення, що в кожній галузі виробництво здійснюється одним технологічним способом або галузі випускають однорідну продукцію. Нехай проміжна продукція і-ї галузі дорівнює
 ,
,
де Xj - валова продукція j-ї галузі,  , Аij - кількість продукції і-ї галузі, яка витрачається на виробництво одиниці продукції j- ї галузі.
, Аij - кількість продукції і-ї галузі, яка витрачається на виробництво одиниці продукції j- ї галузі.
Модель Леонтьєва характеризується виробничою матрицею А
A=(Aij),  ;
;  .
.
Ця матриця також називається матрицею коефіцієнтів прямих матеріальних витрат.
В матрично-векторній формі модель має вигляд
(I-A) =
= ,
,
де I – одинична матриця розміром (n×n),
 - вектор валової продукції (вектор випуску),
- вектор валової продукції (вектор випуску),
 - вектор кінцевої продукції.
- вектор кінцевої продукції.
Вектор валової продукції можна знайти за формулою
 =(I-A)-1
=(I-A)-1 ,
,
G=(I-A)-1,
 =G
=G ,
,
де G - обернена матриця Леонтьєва або мультиплікатор Леонтьєва . Матриця G дорівнює
G=(Gij),  ,
,  .
.
Ця матриця називається матрицею коефіцієнтів повних матеріальних витрат. Елемент Gij показує потребу в валовій продукції і-ї галузі для виробництва одиниці кінцевої продукції j -ї галузі.
Задача планування випуску валової продукції є перетворенням вектора кінцевої продукції  за допомогою матриці (I-A)-1 у вихідний вектор валової продукції
за допомогою матриці (I-A)-1 у вихідний вектор валової продукції 
 =(I-A)-1
=(I-A)-1 .
.
Виникає питання відносно умов, за яких існує така матриця (I-A)-1 , що для будь-якого невід'ємного вектора  ,
,  ≥0, вектор (I-A)-1
≥0, вектор (I-A)-1 також невід'ємний. Матриця А в такому разі називається невід'ємною, якщо всі її елементи є невід'ємними. Для економічних систем матриця А завжди невід'ємна.
також невід'ємний. Матриця А в такому разі називається невід'ємною, якщо всі її елементи є невід'ємними. Для економічних систем матриця А завжди невід'ємна.
Умови продуктивності матриці А зв'язані з використанням одного з тверджень:
-
максимальне власне число λ(A) матриці А менше 1;
-
матриця (I-A) має невід'ємну обернену матрицю;
-
матричний ряд
I+A+A2+...+Ar+… =  ,
,
A0=I,
(так званий ряд Неймана матриці А) збігається, при цьому його сума дорівнює оберненій матриці (I-A)-1
 =(I-A)-1,
=(I-A)-1,
-
послідовні головні мінори матриці (I-A) додатні.
За даними А та  побудувати модель Леонтьєва для двох галузей та знайти вектор валової продукції
побудувати модель Леонтьєва для двох галузей та знайти вектор валової продукції  .
.
Для цього виконати такі дії:
-
знайти матрицю (I-A), де І – одинична матриця
I= ,
,
-
обчислити визначник матриці |I-A|.
Для обчислення визначника можна скористатись правилом трикутника. Наприклад, для матриці В
В= ,
,
визначник дорівнює:
 ,
,
-
знайти мінори для елементів матриці (I-A). Нагадаємо визначення мінору. Мінором Mik називається визначник (n-1) порядку, який одержуємо після викреслення і - рядка та k - стовпця,
![]() ;
; ![]() . Наприклад, мінор М11 дорівнює.
. Наприклад, мінор М11 дорівнює.
 ;
;
-
знайти алгебраїчні доповнення для елементів матриці (I-A).
Позначимо алгебраїчне доповнення  ,
, ;
;  . Алгебраїчним доповненням
. Алгебраїчним доповненням  називається мінор, який береться зі знаком (-1)i+k
називається мінор, який береться зі знаком (-1)i+k


П

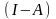 , приєднану до матриці (І-А). Матриця
, приєднану до матриці (І-А). Матриця 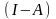 утворюється алгебраїчними доповненнями;
утворюється алгебраїчними доповненнями;

-
транспонувати матрицю
![]() ,
, -
знайти обернену матрицю (І-А)-1 за формулою

 ,
,
-
знайти вектор валової продукції
 =(І-А)-1
=(І-А)-1 ,
,
-
знайти міжгалузеві потоки продукції за формулою
Xij=AijXj,
(i,j)=1,2.
Результати звести до таблиці 4.1
Таблиця 4.1-
Результати розрахунків за моделлю Леонтьєва
| Виробляючі галузі | Споживаючі галузі | Кількість кінцевої продукції | Кількість валової продукції | ||
| 1 | 2 | ||||
| 1 | |||||
| 2 | |||||
4.4 Дослідження моделей міжгалузевих балансів
Модель міжгалузевих балансів на відміну від моделі "витрати-випуск" Леонтьєва містить ще деякі дані. В табл. 4.2. наведена загальна схема міжгалузевого балансу виробництва та розподілення продукції.
Ця схема включає чотири квадранти. Перший квадрант – це шахматна таблиця міжгалузевих потоків продукції. В другім квадранті показана кінцева продукція усіх галузей. Третій квадрант характеризує умовно-чисту продукцію, до якої відносяться амортизаційні відрахування, оплата праці, чистий доход, тощо. Складові третього квадранту можна знайти за формулою
Ei=Xi- ,
,  .
.
Четвертий квадрант знаходиться на перетині стовпця другого квадранту та рядку третього квадранту. Він складається із одного показника і служить для контролю правильності розрахунків: сума елементів другого квадранту має дорівнювати сумі елементів третього квадранту.
Користуючись даними попереднього підрозділу розробити схему міжгалузевого балансу виробництва та розподілення продукції.
Виділяють модифікації моделі міжгалузевого балансу. Для побудови міжгалузевого балансу витрат праці (табл. 4.3) необхідно задати кількість трудових ресурсів
Таблиця 4.2
Міжгалузевий баланс виробництва та розподілення продукції
| Виробляючі галузі | Споживаючі галузі | Кількість Кінцевої продукції | Кількість валової продукції | |||
| 1 | 2 | |||||
| 1 2 | X11 X21 | X12 X22 I | Y1 Y2 II | X1 X2 | ||
| Кількість умовно-чистої продукції | E1 | E2 III | IV | |||
| Кількість валової продукції | X1 | X2 | ||||
Tаблиця 4.3
Міжгалузевий баланс витрат праці
| Виробля ючі галузі | Споживаючі галузі | |||
| Міжгалузеві витрати упредметненої праці | Витрати праці на кінцеву про дукцію | Витрати праці в галузях (трудові ресурси) | ||
| 1 | 2 | |||
| 1 | M11 | M12 | M1 |
|
| 2 | M21 | M22 | M2 |
|
Для пошуку коефіцієнтів прямої трудомісткості можна використати формулу

де  - кількість трудових ресурсів, необхідних для виробництва продукції j-ї галузі,
- кількість трудових ресурсів, необхідних для виробництва продукції j-ї галузі,  - обсяг валової продукції j-ї галузі.
- обсяг валової продукції j-ї галузі.
Вектор-рядок коефіцієнтів повної трудомісткості знаходимо за формулою

де G – матриця повних матеріальних витрат,  - вектор-рядок коефіцієнтів прямої трудомісткості
- вектор-рядок коефіцієнтів прямої трудомісткості  .
.
Помножуючи всі рядки першого та другого квадрантів міжгалузевого балансів на відповідні коефіцієнти прямої трудомісткості, одержуємо схему міжгалузевого балансу витрат праці. Тепер повинно виконуватись рівняння
 .
.
На основі міжгалузевого балансу виробництва та розподілення продукції (табл.4.2) побудувати міжгалузевий баланс витрат праці (табл.4.3). Використати таку кількість трудових ресурсів: 120i люд.-днів та 200i люд.-днів, де і – номер заданого варіанту.
4.5 Дослідження моделі Неймана
Модель Неймана на відміну від моделі Леонтьєва, в якій розглядається тільки один виробничий цикл, носить динамічний характер.
В моделі Неймана розглядається економіка, яка описується базисними виробничими процесами (галузями або підприємствами).

Кожен базисний процес можна зобразити в вигляді
 (
( ),
),  ,
,
де  - вектор витрат,
- вектор витрат,  - вектор випуску. Зміст процесу
- вектор випуску. Зміст процесу  такий: він витрачає вектор
такий: він витрачає вектор  =(a'ij),
=(a'ij),  , та випускає вектор
, та випускає вектор  =(x'ij),
=(x'ij),  , тобто переробляє вектор
, тобто переробляє вектор  в вектор
в вектор  . Ці вектори невід'ємні. Позначимо через A' та X' матриці
. Ці вектори невід'ємні. Позначимо через A' та X' матриці
A'=( ),
),
X'=( ).
).
Модель задається парою невід'ємних матриць A' та X'. Матриця A' називається матрицею витрат, матриця X' - матрицею випуску.
Комбінуючи базисні процеси, можна одержати нові виробничі процеси. Якщо взяти невід'ємний вектор-стовпець  ,
,  , то можна описати новий виробничий процес
, то можна описати новий виробничий процес

в якому витрати характеризує вектор  , а випуск – вектор
, а випуск – вектор  .
.
Нові процеси показують режим спільної роботи різних галузей. Отриманий виробничий процес позначимо (A' ,X'
,X' ) .
) .
Вектор-стовпець  називається вектором інтенсивностей.
називається вектором інтенсивностей.
















