151268 (594656), страница 4
Текст из файла (страница 4)
1.11. Контроль системы
Правильность работы программы МД контролировалась с помощью закона сохранения энергии:
| | (13) |
, где 
- кинетическая энергия атомов системы; 
- потенциальная энергия их взаимодействия; 
- работа, произведенная над системой. Выполнение закона сохранения энергии очень важно при исследовании пластичности твердых тел. Это связано с тем, что хотя тепловое равновесие устанавливается быстро, но установление механического равновесия требует большого времени. Поэтому при деформировании система находится в тепловом равновесии, но скорее не находится в механическом равновесии, т.е. является неравновесной. Следовательно, потеря или приход энергии, вследствие невыполнения закона сохранения энергии, может существенно повлиять на характер поведения системы при деформации.
Неточное сохранение энергии связано в основном с ошибками, возникающими из-за конечного шага интегрирования по времени, а также с ошибками, возникающими из-за конечной точности представления чисел в компьютере.
Оба типа ошибок можно уменьшить, уменьшая шаг интегрирования по времени, что, однако, увеличивает время вычислений.
Другой тип ошибок возникает из-за использования потенциала с обрезанием. Скачок потенциала на радиусе обрезания при пластической деформации, когда атомы могут двигаться друг относительно друга, приводит к значительному нарушению закона сохранении энергии. Использование потенциала без скачка (3) позволяет существенно улучшить выполнения закона сохранения энергии. Потенциал (3), однако, имеет скачок производной (силы) на радиусе обрезания 
. Это также приводит к несоблюдению закона сохранения энергии. Оно особенно ярко проявляется при уменьшении радиуса обрезания от канонических значений 
и 
. Это связанно с тем, что канонические значения радиуса обрезания находятся в минимумах радиального распределения атомов гексагональной решетки. Когда же попадает в максимум радиального распределения число атомов, то испытывающих действие силы (при 
), то прекращающих испытывать ее действие (при 
), становиться очень большим, что и приводит к существенному несохранению энергии. Чтобы избавиться от скачка производной потенциала на радиусе обрезания потенциал был модернизирован. Пусть
| | (14) |
,где
| | (15) |
и 
, 
, 
. Тогда модернизированный потенциал имеет вид
| | (16) |
Модернизированный потенциал гладко сшивается (до второй производной) с потенциалом Леннарда-Джонса на радиусе сшивки 
и зануляется вместе со своей первой производной на радиусе обрезания . С этим потенциалом при значениях параметров 
и 
были проведены все расчеты в данной работе.
1.12. Вычисление физических величин
При деформировании системы все физические величины, такие как напряжение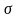 
, температура 
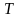, кинетическая энергия 
, потенциальная энергия 
характеризующие деформируемую систему меняются. Их мгновенные значения, усредненные по малым промежуткам времени чтобы исключить тепловые колебания, описывают состояние деформируемой системы. В отличие от равновесных систем мы не можем теперь использовать усреднение по времени, а должны использовать усреднение по различным начальным состояниям системы.
Кинетическая и потенциальная энергия находятся как
| | (17) | |
| | (18) |
Температура определяется как
| | (19) |
, где 
- размерность системы. В двухмерном случае 
- средней кинетической энергией. Выражение для тензора напряжений, основанное на вириальной теореме [14,15], имеет вид
| | (20) |
, где 
- 
-компоненты тензора напряжений для атома 
, 
- объем, приходящийся на атом (
, где 
- полный объем системы), 
- масса атома , 
- 
-компонента его импульса, 
- расстояние между атомами и 
(
- компонента вектора, направленного от -го атома к -му атому). Это выражение для тензора напряжений не единственное, существуют и другие его определения. Однако, когда напряжения усредняются по объему различные определения быстро сходятся к макроскопическому полю напряжений. Во время моделирования кривые напряжение - деформация строятся после усреднения атомного напряжения по всей системе.
1.13. Визуализация
МД позволяет получать огромные объемы информации, описывающие исследуемую систему во всех деталях. Поэтому возникает задача, извлечь из этого моря информации нужную информацию и предоставить ее в виде, удобном для восприятия. Например, увидеть дефекты находящиеся внутри трехмерного кристалла, невозможно, поскольку их закрывают атомы, находящиеся на том же луче зрения, но ближе к наблюдателю. Однако, оставив только атомы, окружающие дефекты и удалив все остальные, это можно легко сделать. Другая возможность состоит в использовании анимации для исследования временной эволюции деформируемой системы.
Во время деформирования кристаллов упорядоченное расположение атомов кристалла нарушается, появляются дефекты. Для исследования локального атомного порядка обычно используется алгоритм, известный как Common Neighbor Analysis (CNA) [16,17]. Для того чтобы определить структуру кристалла в этом алгоритме исследуются связи между атомами и его соседями. Два атома считаются связанными, если расстояние между ними меньше критического расстояния, выбранного между первыми двумя пиками в радиальной функции распределения. Связи классифицируются с помощью трех целых чисел 
. Первое из них, , есть число общих соседей, т.е. атомов, связанных с обоими атомами в рассматриваемой связи. Второе, , есть число связей между этими общими соседями. Третье, 
, есть самая длинная цепочка, которую можно образовать из этих связей.
Число и тип связей, которые имеет атом, определяют локальную кристаллическую структуру. Например, атомы в совершенном ГЦК кристалле имеет 12 связей типа 421, тогда как в совершенном ГПУ кристалле имеют 6 связей типа 421 и 6 типа 422.
Использование CNA позволяет сделать видимыми при моделировании дислокации, границы зерен и дефекты упаковки. Например, при деформировании кристаллов меди, с помощью CNA классифицируют атомы на три класса: ГЦК, ГПУ и “другие”, где в класс “другие” попадают атомы, которые имеют число связей, отличное от 12, или тип их связей отличен от 421 и 422. Тогда внутренние дефекты упаковки видны как две сопряженные (111) плоскости ГПУ атомов, несвойственные дефекты упаковки видны как две (111) плоскости атомов ГПУ, разделенных (111) плоскостью атомов ГЦК. Границы двойников видны как одиночные (111) плоскости ГПУ атомов. Ядра дислокации и границы зерен состоят из атомов класса “другие”, хотя границы зерен содержат также немного ГПУ атомов.
Тепловые колебания атомов мешают выполнять CNA. Если при моделировании температура сравнительно низкая, достаточно тщательно выбрать критическое расстояние. Для высоких же температур необходимо предварять CNA короткой минимизацией (достаточной чтобы уменьшить тепловые колебания атомов, но избежать движения дислокаций).
В двухмерных системах нет нужды выполнять CNA анализ - дефекты видны непосредственно. Кроме того, в отличие от трехмерных систем, отсутствуют заслоняющие атомы. Поэтому двухмерные системы удобны для анимации, т.е. воспроизведения временной эволюции деформируемой системы. Для создания анимации через заданное число шагов по времени МД, используя координаты атомов, формировалося изображение системы, которое затем сохранялось на жестком диске в bmp-файле. Анимация достигалась выводом этих изображений на экран дисплея в той же последовательности, в которой они создавались. Одно из преимуществ анимации - это наглядность. Поля других физических величин, например, напряжения, температуры, используя подходящую кодировку, также можно использовать для анимации.
2. Моделирования пластической деформации ГПУ-кристаллов
Автором была создана программа для изучения пластичности в двумерных кристаллах. Двумерные системы были выбраны, чтобы обойти проблемы, связанные с высокими требованиями к вычислительным ресурсам в случае трехмерных систем и визуализацией результатов вычислений. Для решения уравнений движения использовался алгоритм Верле со скоростью. В качестве потенциала взаимодействия между атомами был выбран потенциал Леннарда-Джонса. При моделировании вычислительная ячейка растягивалась вдоль умножением ее продольного размера на каждом шаге по времени на масштабный множитель (1+ε), где ε – малое число (0.00001), выбранное так, чтобы обеспечить требуемую скорость деформации. Координаты атомов при этом не менялись, т.е. при этом вводился зазор между атомами в смежных ячейках моделирования. При этом нагрузка прикладывалась к торцам кристалла, что лучше соответствует эксперименту. Поперечный размер системы контролировался с помощью динамического уравнения (12). Перед деформацией система приводилась в равновесное состояние с заданной температурой коротким прогоном с помощью МД. При вычислении кривых напряжение-деформация проводилось усреднение напряжения по атомам всей системы. С помощью закона сохранения энергии контролировалась правильность работы программы. Для наблюдения за временной эволюцией деформируемого кристалла использовалась анимация. Блок-схема программы приведена ниже.
| Задание входных данных
| ||
| Задание начальных значений
| ||
| Достижение равновесного состояния с заданной температурой | ||
| Цикл по атомам (Вычисление начального ускорения) | ||
| Сила Fi, действующая на i-тый атом = сумме сил, действующих со стороны соседних атомов. Ускорение i-того атома ai (t) = Fi/mi | ||
| Конец цикла по атомам | ||
| Цикл по времени (Траектория + растяжение) | ||
| Цикл по атомам (Вычисление нового положения и промежуточной скорости) | ||
|
| ||
| Конец цикла по атомам | ||
| Проверка граничных условий | ||
| Растяжение | ||
| Цикл по атомам (Вычисление нового ускорения и новой скорости ) | ||
| Сила Fi, действующая на i-тый атом = сумме сил, действующих со стороны соседних атомов. Ускорение i-того атома ai (t+Δt) = Fi/mi
| ||
| Конец цикла по атомам | ||
| Контроль параметров
| ||
| Конец цикла по времени | ||
| Визуализация | ||
Программа позволяет проводить как обычную МД, так и использовать процедуру минимизации. Программа позволяет исследовать влияние ориентации кристалла, скорости деформирования и температуры на процесс деформирования. Она также позволяет использовать свободные и периодические граничные условия на боковых, относительно растяжения, сторонах кристалла.
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
