Лабораторная работа №4 (544876), страница 2
Текст из файла (страница 2)
Можно доказать, что у любой конечной игры mn существует решение, в котором число активных стратегий каждой стороны не превосходит наименьшего из чисел m и n. Из этого, в частности, следует, что у игры 2n всегда имеется решение, в котором с каждой стороны участвуют не более двух активных стратегий . Иначе говоря, можно свести игру 2n к игре 22.
Общая схема поиска  :
:
-
по данным платёжной матрицы вычерчивается график функции
![]() и на нём отыскивается экстремальная точка
и на нём отыскивается экстремальная точка ![]() ;
; -
выбираются две прямые пересекающиеся в этой точке
![]() таким образом, чтобы точка пересечения не теряла экстремальных свойств (берутся прямые с противоположным наклоном);
таким образом, чтобы точка пересечения не теряла экстремальных свойств (берутся прямые с противоположным наклоном); -
отвечающие им стратегии B(1), B(2) включаются в игру против A1 и A2;
-
полученная игра 22 решается либо с помощью формул, либо графическим способом.


Очевидно, так же может быть решена и игра m2, с той разницей, что придётся строить прямые
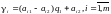 и по ним определить
и по ним определить 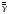 как точную верхнюю границу значений i и на ней ищется не максимум, а минимум (см. рис.4) .
как точную верхнюю границу значений i и на ней ищется не максимум, а минимум (см. рис.4) .Пример. Дана игра 52 (см. табл.), не имеющая седловых точек. Требуется найти оптимальные стратегии сторон.
| A\B | B1 | B2 |
| A1 | 1.5 | -1.5 |
| A2 | 2 | 0 |
| A3 | -1 | 2.5 |
| A4 | 3.5 | -3 |
| A5 | 1 | 2 |
Решение: Строим прямые, определяемые уравнениями  , т.е. 1=3q1-1.5;
, т.е. 1=3q1-1.5;
2=2q1;
3=-3.5q1+2.5;
4=6.5q1-3;
5=-q1+2. (см. рис.5)
Рис.5

Экстремальная точка графика функции
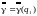 (показан жирной линией) имеет координаты q*10.67; 1.3, и через нее проходят прямые 2, 4, 5. Следовательно, сторона А имеет, вообще говоря, три активные стратегии А2, А4, А5, из которых можно выбрать две, например, А2 и А5 или А4 и А5 . Выбор А2 и А4 исключен, т.к. точка (0.67;1.3) перестает быть экстремальной.
(показан жирной линией) имеет координаты q*10.67; 1.3, и через нее проходят прямые 2, 4, 5. Следовательно, сторона А имеет, вообще говоря, три активные стратегии А2, А4, А5, из которых можно выбрать две, например, А2 и А5 или А4 и А5 . Выбор А2 и А4 исключен, т.к. точка (0.67;1.3) перестает быть экстремальной.Пусть выбираются стратегии А2 и А5. Тогда игра 22 приобретает вид:
| 2 | 0 |
| 1 | 2 |
и для нее по формулам вычисляются p*1=1/3, p*2=2/3, q*1=2/3 q*2=1/3, =4/3.
Если выбираются стратегии А4 и А5, то игра 22 приобретает вид:
| 3.5 | -3 |
| 1 | 2 |
Здесь формулы приводят к результатам p*1=2/15, p*2=13/15, q*1=2/3 q*2=1/3, =4/3.
Таким образом, оптимальными стратегиями сторон являются либо S*A={0,1/3,0,0,2/3}; S*B={2/3,1/3} либо S*A={0,0,0,2/15,13/15}; S*B={2/3,1/3}, при одном и том же значении =4/3.
Задание к лабораторной работе № 4
1)Упростить игру
| 1. | 2. | 3. | 4. | ||
| 5. | 6. | 7. | 8. | ||
| 9. | 10. | 11. | |||
| 12. | 13. | 14. | |||
| 15. | 16. | 17. | |||
| 18. | 19. | ||||
| 20. | 21. | ||||
| 22. | 23. | 24. | |||
2)Решить игру графически и аналитически.
| 1. | 2. | 3. | 4. | 5. | 6. |
| 7. | 8. | 9. | 10. | 11. | 12. |
| 13. | 14. | 16. | |||
| 15. | 17. | ||||
| 18. | 19. | ||||
| 20. | 21. | ||||
| 22. | 23. | ||||
| 24. | |||||
3
 и на нём отыскивается экстремальная точка
и на нём отыскивается экстремальная точка  ;
; таким образом, чтобы точка пересечения не теряла экстремальных свойств (берутся прямые с противоположным наклоном);
таким образом, чтобы точка пересечения не теряла экстремальных свойств (берутся прямые с противоположным наклоном);













 .
.








 .
.


























