Просмтор этого файла доступен только зарегистрированным пользователям. Но у нас супер быстрая регистрация: достаточно только электронной почты!

Текст из файла

11

ЗАДАЧИ

ДЛЯ СТУДЕНТОВ ВМиК

НА 5-й СЕМЕСТР

ЗАДАЧА 1

Исследовать датчик псевдослучайных чисел с равномерным распределением на интервале [0, 1] на равномерность по критерию согласия .

Алгоритм решения задачи.

1. Построить ДСЧ методом вычетов. При построении ДСЧ вводить количество обращений к датчику, стартовое число.

Метод вычетов:

нечетное

1. Построить статистический ряд. При построении статистического ряда вводить количество интервалов. Организовать вывод на экран дисплея номеров интервалов и количество попаданий случайной величины в каждый интервал .

2. Вычисляется величина и выводится на экран.

1. По таблице находится

2. Производится сравнение и и принимается решение о качестве датчика случайных числе.

ЗАДАЧА 2

Построить и проверить ДСЧ, распределенных по экспоненциальному закону, методом обратных функций и методом Неймана.

Дана плотность распределения случайной величины:

Моделирование Последовательности Случайных Чисел производить путем использования 2-х методов: метода обратных функций и метода Неймана.

Чтобы проверить полученные датчики, сравниваем теоретические и практические значения МОЖ и дисперсии для двух вариантов.

для устранения смещенности , где N – выборка ПСЧ, распределенных по экспоненциальному закону.

ПРИМЕЧАНИЕ 1) В качестве датчика равномерного распределения использовать датчик из ЗАДАЧИ №1

2) Ввод исходных данных осуществлять в диалоговом режиме

ЗАДАЧА 3

Моделирование ПСЧ с нормальным законом распределения и проверить по критерию Пирсона.

Основная часть.

Нормальные случайные числа получаются путем выбора чисел, распределенных равномерно, и использования их затем в качестве ординат функции нормального распределения вероятностей. Величины соответствующих абсцисс представляют собой числа, распределенные по нормальному закону.

Получение нормальных чисел может быть вполне надежно, по крайней мере, для значений в интервале и осуществлено с привлечением Центральной Предельной Теоремы.

Случайное сило x может быть получено следующим образом:

– случайное число, равномерно распределение в интервале [0, 1].

n – количество .

Проверку по критерию осуществляют следующим образом:

1. Весь интервал значений ПСЧ (от до ) разбивается на k интервалов.

2. Подсчитывается – количество попаданий ПСЧ в i-ый интервал. i=(1-k)

3. Находится величина – теоретическая частота попаданий ПСЧ в i-ый интервал.

, где

1. Подсчитывается , где N – выборка ПСЧ.

2. Задавая и z , находят (теоретическое). Проверяют условие  , если условие не выполняется, то гипотеза о нормальности датчика признается несостоятельной.

3. Для контроля правильности решения задачи необходимо рассчитать среднестатистическое мат. ожидание и дисперсию и сравнить с исходными

4. Программа функции erf дается в приложении.

Приложение

Функция erf вычисляется по одному из способов:

1. .

ПРИМЕЧАНИЕ 1) В качестве датчика равномерного распределения использовать датчик из ЗАДАЧИ №1

2) Ввод исходных данных осуществлять в диалоговом режиме

ЗАДАЧА 4

Оценка боевой эффективности образцов вооружения при стрельбе по одиночной цели.

Боевой эффективностью образца вооружения целесообразно считать поражение цели, т.е. W= .

Основная часть

где

G(x,y,z) — координатный закон поражения,

f(x,y,z) — закон рассеивания точек подрыва.

1. Определение закона рассеивания.

В случае, если взрыватель неконтактный — в главных осях

Практические измерения на полигонах позволяют считать закон рассеивания нормальным при линейной зависимости от распределения по z (в картинной плоскости), т.е. , где — константы, — параметры закона рассеивания.

1. Определение координат закона поражения.

Для вычисления G(x,y,z) полагаем, что цель представляет собой цилиндр диаметром 2a и длиной 2b ось z проходит через середину цилиндра. Боевую часть образца вооружения считаем осколочно-фугасной.

З она поражения вокруг цели имеет вид:

X,Y

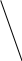
2a

2b

Z

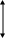
f1

f2

Z

При этом вид координатного закона поражения внутри зоны поражения имеет вид:

k — характеристика плотности потока осколков.

1. Рекомендации по алгоритмизации:

Определение W сводится к вычислению тройного интеграла от произведения двух функций по всему объему.

а) Закон рассеивания считаем нормальным, при этом в пределах параллелепипеда с размерами по соответствующим осям заключено 94% всех значений W, т.е. с небольшой потерей можно вычислять значения f(x,y,z) в этом параллелепипеде;

б) Вне зоны поражения вероятность поражения равна нулю, т.е. вычисление интеграла достаточно вести в области, представляющей собой пересечение " -параллелепипеда" с зоной поражения;

в) Вычисления целесообразно проводить методом статистических испытаний.

Используем равномерно распределенные случайные величины и вычисляем эффективность по математическому ожиданию.

1. Проведем N испытаний, в каждом i-ом из которых разыгрываем случайную и равномерную величину , .

Вычисляем параметры закона рассеивания по z для полученных

, затем

.

После выполнения испытаний вычисляется значение интеграла для

ИСХОДНЫЕ ДАННЫЕ:

1. — параметры закона рассеивания

2. a,b- параметры цели.

3. , - постоянные определяющие линейную зависимость

3) f1, f2, - углы переднего и заднего фронтов разлета осколков.

4) k=10000 — характеристика плотности потока осколков.

5) - радиус фугасного поражения.

ПРИМЕЧАНИЕ: 1) Ввод исходных данных осуществлять в диалоговом режиме

2) В качестве датчика равномерного распределения использовать датчик из ЗАДАЧИ №1

ЗАДАЧА 5

Вычисление показателей эффективности стрельбы по рассредоточенной групповой цели без переноса огня методом статистических испытаний.

Постановка задачи.

Каждая единица групповой цели обстреливается независимо от других "обобщенным" выстрелом и поражается с вероятностью , где M— количество целей в группе.

Определить:

1. Вероятность поражения не менее k единиц.

2. Среднее число пораженных единиц.

Исходные данные

• Общее количество целей (M);

• Количество сбитых целей (k);

• Количество испытаний (N);

• Вероятность поражения каждой из целей обобщенным выстрелом .

ПРИМЕЧАНИЕ: 1) Ввод исходных данных осуществлять в диалоговом режиме

2) В качестве датчика равномерного распределения использовать датчик из ЗАДАЧИ №1

ЗАДАЧА 6

Вычисление показателей эффективности стрельбы по рассредоточенной групповой цели без переноса огня методом, использующим двоичную переменную.

Постановка задачи.

Каждая единица групповой цели обстреливается независимо от других "обобщенным" выстрелом и поражается с вероятностью , где M— количество целей в группе.

Определить:

Вероятность поражения не менее k единиц из M, где .

ПРИМЕЧАНИЕ: 1) Ввод исходных данных осуществлять в диалоговом режиме

ЗАДАЧА 7

Оценка эффективности РЛС как системы массового

обслуживания методом статистических испытаний.

ПОСТАНОВКА ЗАДАЧИ:

Радиолокационная станция (РЛС) имеет пять однотипных каналов обслуживания заявок (n=5). В зоне обнаружения РЛС появляются цели со средней плотностью =…^сам/_мин. Время обслуживания каждого самолета известно и равно T_обс=… мин. Рассматривая РЛС как систему массового обслуживания (СМО) с отказами, необходимо методом статистических испытаний определить вероятности состояний системы P_i (i=0…5), среднее число занятых каналов N_ср и вероятность прорыва цели P_пр.

ДАНО:

n = 5 - число каналов;

 = 5 ^сам/_мин - средняя плотность поступления заявок;

T_обс = … мин - время обслуживания одной заявки (вводится по заданию преподавателя);

N = 5000 - число испытаний;

ОПРЕДЕЛИТЬ: методом стат. испытаний.

P ₀ = ?

P₁ = ? вероятности

P₂ = ? состояний

P₃ = ? системы

P₄ = ?

P₅ = ?

N_ср = ? - среднее число занятых каналов

P_пр = ? - вероятность прорыва цели

Примечание: при написании программы предусмотреть ввод значений T_обс и  по запросу программы.

1) Число занятых каналов определять в момент поступления заявки.

2) В качестве датчика равномерного распределения использовать датчик из ЗАДАЧИ №1

Характеристики

Тип файла документ

Документы такого типа открываются такими программами, как Microsoft Office Word на компьютерах Windows, Apple Pages на компьютерах Mac, Open Office - бесплатная альтернатива на различных платформах, в том числе Linux. Наиболее простым и современным решением будут Google документы, так как открываются онлайн без скачивания прямо в браузере на любой платформе. Существуют российские качественные аналоги, например от Яндекса.

Будьте внимательны на мобильных устройствах, так как там используются упрощённый функционал даже в официальном приложении от Microsoft, поэтому для просмотра скачивайте PDF-версию. А если нужно редактировать файл, то используйте оригинальный файл.

Файлы такого типа обычно разбиты на страницы, а текст может быть форматированным (жирный, курсив, выбор шрифта, таблицы и т.п.), а также в него можно добавлять изображения. Формат идеально подходит для рефератов, докладов и РПЗ курсовых проектов, которые необходимо распечатать. Кстати перед печатью также сохраняйте файл в PDF, так как принтер может начудить со шрифтами.

Список файлов курсовой работы