Пусть даны два ряда и , где , и для всех n . Тогда, - Ответ на вопрос по математике №979819
-16%
Вопрос
Пусть даны два ряда и , где , и для всех n . Тогда, если ряд сходится, то сходится и ряд , а если ряд расходится, то расходится и ряд :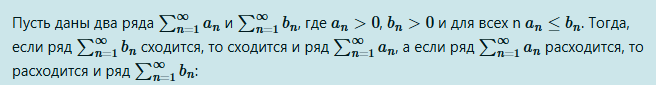
- признак сравнения
- признак Коши
- необходимое условие сходимости
- признак Даламбера
- признак Лейбница
Ответ
Этот вопрос в коллекциях
Коллекция: Математика
249 руб.
Если нужен другой вариант работы или отдельная задача из любой работы, пишите в комментарии
![](https://s.studizba.com/z.php?f=/templates/si/i/noavatar.png&w=100&h=100&t=1"){kind=avatar}
