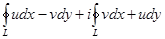Доказать основную теорему Коши для односвязной области
Доказать основную теорему Коши для односвязной области
Интегральная теорема Коши (для односвязной области).
Пусть G – односвязная область, пусть функция f(z) – аналитическая в G функция, пусть L – кусочно—гладкий контур, принадлежащий области G. Тогда  .
.
Теорему можно сформулировать и так: интеграл от аналитической функции вдоль кусочно-гладкого контура равен нулю.
Доказательство.
|
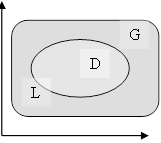
| Обозначим D – внутренность контура L . Запишем формулу Грина |
Применим к каждому слагаемому в правой части равенства формулу Грина. В первом интеграле примем P = u, Q = -v.

Рекомендуемые материалы
(для аналитической функции выполнены условия Коши – Римана  ).
).
Во втором интеграле примем P = v, Q = u.
 (условие Коши – Римана).
(условие Коши – Римана).
Поэтому  .
.
Следствие. Пусть L1, L2 – две кусочно-гладких дуги в односвязной области G, соединяющие точки A, B. Пусть функция f(z) – аналитическая в области G. Тогда  =
=  .
.
Можно дать словесную формулировку: интеграл от аналитической функции в односвязной области вдоль кусочно-гладкой дуги не зависит от формы дуги, а зависит только от начальной и конечной точек дуги.
Доказательство. Образуем контур  . По интегральной теореме Коши
. По интегральной теореме Коши
 . Но
. Но  . Следовательно,
. Следовательно,  .=
.=  .
.
Поэтому результат в рассмотренном выше примере не случаен.
Очень важный пример. Вычислить интеграл  , где n – целое число, контур
, где n – целое число, контур  - окружность с центром в точке
- окружность с центром в точке  радиусом
радиусом  .
.
Покажем, что точки z на контуре можно описать уравнением
можно описать уравнением  ,
,  ,
,  - действительное число. В самом деле,
- действительное число. В самом деле,  , так как
, так как  . Таким образом, контур
. Таким образом, контур  - это геометрическое место точек комплексной плоскости, расположенных на расстоянии
- это геометрическое место точек комплексной плоскости, расположенных на расстоянии  от точки
от точки  - окружность с центром в точке
- окружность с центром в точке  радиусом
радиусом  .
.
Если  , то подынтегральная функция – аналитическая внутри контура
, то подынтегральная функция – аналитическая внутри контура  . Тогда по интегральной теореме Коши
. Тогда по интегральной теореме Коши  = 0.
= 0.
15 Земский собор на Руси - лекция, которая пользуется популярностью у тех, кто читал эту лекцию.
Пусть  . Так как точка z лежит на контуре
. Так как точка z лежит на контуре  , то
, то  ,
,  . Перейдем к переменной
. Перейдем к переменной  . Пусть
. Пусть  .
.
 =
= 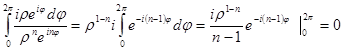
по периодичности экспоненты.
Пусть  . Тогда
. Тогда
 =
= .
.
Вывод.  =
= .
.



 . Представим интеграл
. Представим интеграл  в первой форме записи через два криволинейных интеграла
в первой форме записи через два криволинейных интеграла