Двумерные случайные величины
Лекция 6.
Двумерные случайные величины
Совокупность двух случайных величин (X,Y), заданных на вероятностном пространстве  , называют двумерной случайной величиной или двумерным случайным вектором, X,Y называют координатами случайного вектора.
, называют двумерной случайной величиной или двумерным случайным вектором, X,Y называют координатами случайного вектора.
Это определение можно обобщить и на совокупность n случайных величин.
Функцией распределения случайного вектора (X,Y) или совместной функцией распределения случайных величин X,Y называется
 .
.
Свойства функции распределения.
1  (Это – свойство вероятности, а
(Это – свойство вероятности, а  - вероятность).
- вероятность).
Рекомендуемые материалы
2  - неубывающая функция по каждому из своих аргументов. (В самом деле, если
- неубывающая функция по каждому из своих аргументов. (В самом деле, если  , то событие
, то событие  включено в событие
включено в событие  , следовательно, его вероятность меньше)
, следовательно, его вероятность меньше)
3  (события
(события 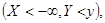
 - невозможные, поэтому их вероятность равна нулю).
- невозможные, поэтому их вероятность равна нулю).
4  (событие
(событие  достоверно).
достоверно).
5  =
=  -
-  -
-  +
+ 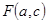
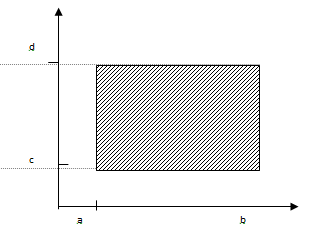
Геометрически,  - площадь полосы левее и ниже точки
- площадь полосы левее и ниже точки  , Вычитая из нее
, Вычитая из нее  и
и  , мы два раза вычтем площадь полосы левее и ниже точки
, мы два раза вычтем площадь полосы левее и ниже точки  . Для того, чтобы получить площадь прямоугольника – левую часть равенства, надо вычитать эту площадь один раз, поэтому надо добавить ее, т.е.
. Для того, чтобы получить площадь прямоугольника – левую часть равенства, надо вычитать эту площадь один раз, поэтому надо добавить ее, т.е. 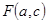 в правую часть равенства.
в правую часть равенства.
6.  непрерывна слева по каждому из аргументов
непрерывна слева по каждому из аргументов
7.  . Так как событие
. Так как событие  достоверно, то пересечение событий
достоверно, то пересечение событий  и
и  есть событие
есть событие  . Поэтому первое равенство справедливо. Аналогично доказывается справедливость второго равенства.
. Поэтому первое равенство справедливо. Аналогично доказывается справедливость второго равенства.
Двумерная случайная величина (X,Y) дискретна, если X, Y - дискретные случайные величины. Для нее составляется таблица распределения – аналог ряда распределения для одномерной случайной величины.
| X | Y | ||||
| y1 | y2 | ….. | ym | PX | |
| x1 | p11 | p12 | … | p1m | pX1 |
| x2 | p21 | p22 | … | p2m | pX2 |
| ……. | … | … | … | … | … |
| xn | pn1 | pn2 | … | pnm | pXn |
| PY | pY1 | pY2 | … | pYm |
Здесь pnm =  , pYm =
, pYm =  = p1m+ p2m +…+pnm,
= p1m+ p2m +…+pnm,
pXn = pn1 + pn2 + … +pnm.
График функции распределения для двумерной случайной величины напоминает «лестницу», уровень ступеней которой изменяется скачком на pij при переходе через точку (xi , yj) в положительном направлении по оси OX и по оси OY. Если зафиксировать x = xi, то при увеличении y эти скачки будут на pi1, pi2, … pim (от нуля до pXi ). Если зафиксировать y = yj, то при увеличении x скачки будут на p1j, p2j, … pnj (от нуля до pYj). Нижние ступени (при x x1 и y
x1 и y y1) находятся на нулевом уровне, самая верхняя ступень (при x>xn, y>ym) находится на уровне 1. Если зафиксировать x > xn то при увеличении y эти скачки будут на pY1, pY2, … pYm (от нуля до 1). Если зафиксировать y > ym, то при увеличении x скачки будут на pX1, pX2, … pXn (от нуля до 1).
y1) находятся на нулевом уровне, самая верхняя ступень (при x>xn, y>ym) находится на уровне 1. Если зафиксировать x > xn то при увеличении y эти скачки будут на pY1, pY2, … pYm (от нуля до 1). Если зафиксировать y > ym, то при увеличении x скачки будут на pX1, pX2, … pXn (от нуля до 1).
Пример. Проводятся два выстрела в мишень. При каждом выстреле вероятность попадания p, вероятность промаха q = 1- p. Случайная величина Xi – число попаданий при i – том выстреле. Найдем закон распределения случайного вектора (X1, X2)= .
.
| X | Y | ||
| y1=0 | y2=1 | PX | |
| x1=0 | q2 | qp | pX1=q |
| x2=1 | pq | p2 | pX2=p |
| PY | pY1=q | pY2=p |
Построим функцию распределения
 . В самом деле, при
. В самом деле, при  – событие{X<x,Y<y} - невозможное, при (x>1, y>1) событие {X<x,Y<y} – достоверное.
– событие{X<x,Y<y} - невозможное, при (x>1, y>1) событие {X<x,Y<y} – достоверное.
При  событие {X<x,Y<y} представляет собой событие {X=0,Y=0}. Поэтому при
событие {X<x,Y<y} представляет собой событие {X=0,Y=0}. Поэтому при  F(x) = P{X=0,Y=0}= q2.
F(x) = P{X=0,Y=0}= q2.
При  событие {X<x,Y<y} представляет собой объединение несовместных событий {X=0,Y=0} и {X=0,Y=1}. Поэтому при
событие {X<x,Y<y} представляет собой объединение несовместных событий {X=0,Y=0} и {X=0,Y=1}. Поэтому при  F(x) =. P{X=0,Y=0}+ P{X=0,Y=1}= q2 + pq = q(p+q)=q.Аналогично, в случае
F(x) =. P{X=0,Y=0}+ P{X=0,Y=1}= q2 + pq = q(p+q)=q.Аналогично, в случае  F(x) = P{X=0,Y=0}+ P{X=1,Y=0}= q2 + pq = q(p+q)=q
F(x) = P{X=0,Y=0}+ P{X=1,Y=0}= q2 + pq = q(p+q)=q
Двумерная случайная величина непрерывна, если X, Y, непрерывные случайные величины и ее функцию распределения можно представить в виде сходящегося несобственного интеграла от плотности распределения.
 .
.
Двойной интеграл можно записать в виде повторных (внешний по x, внутренний по y и наоборот). Если предполагать непрерывность плотности по x и y, то, дифференцируя по переменным верхним пределам, получим
 .
.
Свойства плотности.
1.  (функция распределения – неубывающая функция).
(функция распределения – неубывающая функция).
2.  (по свойству 5 функции распределения) Справедливо обобщение
(по свойству 5 функции распределения) Справедливо обобщение  .
.
3. 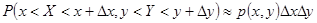
4.  (по свойству 4 функции распределения)
(по свойству 4 функции распределения)
5. 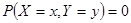
6. 
 ,
,  (Свойство 7 функции распределения)
(Свойство 7 функции распределения)
Независимость случайных величин.
Случайные величины X, Y называются независимыми, если  , где
, где  - функции распределения случайных величин X, Y.
- функции распределения случайных величин X, Y.
Если случайные величины непрерывны, то, дифференцируя это соотношение по x, y, получим  .
.
Соотношение  поэтому можно считать определением независимости непрерывных случайных величин.
поэтому можно считать определением независимости непрерывных случайных величин.
Для дискретных случайных величин определение независимости можно записать в виде  .
.
Математическое ожидание.
Математическим ожиданием функции двумерной случайной величины называется
 в дискретном случае,
в дискретном случае,
 в непрерывном случае.
в непрерывном случае.
Свойства математического ожидания
1.  (
( по условию нормировки)
по условию нормировки)
2. 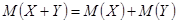
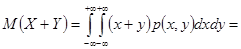
 =
= 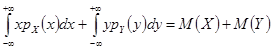
3  для независимых случайных величин.
для независимых случайных величин.
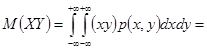

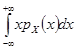
 =
=  .
.
Ковариация (корреляционный момент).
Ковариацией случайных величин называют  .
.
Свойства ковариации.
1. 
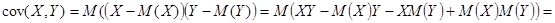
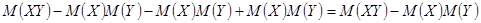
2. 
По свойству 1 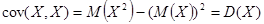
3. Если X, Y независимы, то  , (обратное неверно).
, (обратное неверно).
Если случайные величины независимы, то  , тогда по свойству 1
, тогда по свойству 1  .
.
Случайные величины называются некоррелированными, если  , из некоррелированности не следует независимость, из независимости следует некоррелированность.
, из некоррелированности не следует независимость, из независимости следует некоррелированность.
4. 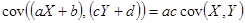
По свойству 1
 =
= =
=  =
=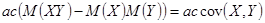
5. 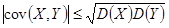
Рассмотрим случайную величину  .
. 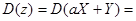
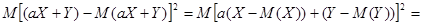
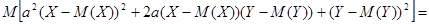
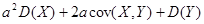 .
.
Заметим, что отсюда следует свойство дисперсии (при a =1)
 .
.
Так как  , то
, то 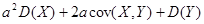
 . Это возможно только, если дискриминант этого квадратного трехчлена относительно a меньше или равен нулю. Выпишем это требование к дискриминанту:
. Это возможно только, если дискриминант этого квадратного трехчлена относительно a меньше или равен нулю. Выпишем это требование к дискриминанту:
 . Отсюда следует свойство 5.
. Отсюда следует свойство 5.
6. Для того, чтобы случайные величины были линейно зависимы (Y = aX +b), необходимо и достаточно, чтобы 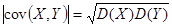
Необходимость. Пусть Y=aX+b. Тогда 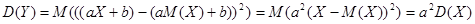
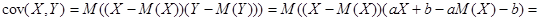
 =
=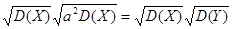
Достаточность. Пусть 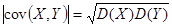 . Тогда (доказательство свойства 5)
. Тогда (доказательство свойства 5)  следовательно, z -
следовательно, z - детерминированная величина, т.е.
детерминированная величина, т.е.  , поэтому величины X, Y – линейно зависимы.
, поэтому величины X, Y – линейно зависимы.
Коэффициентом корреляции называется  .
.
Свойства коэффициента корреляции.
1. 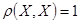
2. Если X, Y – независимы, то 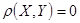
3. 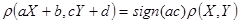
4. 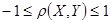
5.  тогда и только тогда, когда X,Y линейно зависимы.
тогда и только тогда, когда X,Y линейно зависимы.
Двумерное равномерное распределение
Случайный вектор (X, Y) равномерно распределен в области D (площадь D равна S), если его плотность распределения задана так: p(x,y) = 0, если x Ï D, p(x,y) = 1/S, если xÎD.
Пример. Случайный вектор (X,Y) равномерно распределен в прямоугольнике 0£x£a, 0£x£b.
 , аналогично
, аналогично  .
.
 , аналогично
, аналогично  .
.
 , аналогично
, аналогично  .
.
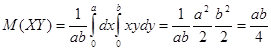
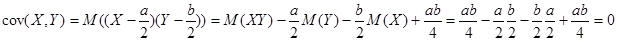
Следовательно, случайные величины X, Y не коррелированны.
Двумерное нормальное распределение
Двумерная случайная величина (X,Y) распределена нормально со средними значениями m, m2, дисперсиями  и коэффициентом корреляции
и коэффициентом корреляции  , если ее плотность задана:
, если ее плотность задана:

Задача линейного прогноза.
Заданы характеристики  случайного вектора
случайного вектора  . Вводится случайная величина – оценка
. Вводится случайная величина – оценка  - линейный прогноз. Вычислить
- линейный прогноз. Вычислить  , чтобы линейный прогноз был наилучшим среднеквадратическим (в смысле минимума погрешности оценки:
, чтобы линейный прогноз был наилучшим среднеквадратическим (в смысле минимума погрешности оценки: ).
).
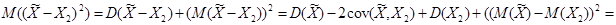
Люди также интересуются этой лекцией: 18.1 Внешняя политика СССР и международные отношения в 1930-е гг.
 .
.
За счет выбора  можно лишь минимизировать последнее слагаемое, сделав его нулем:
можно лишь минимизировать последнее слагаемое, сделав его нулем:  .Теперь остается обеспечить минимум квадратного трехчлена от
.Теперь остается обеспечить минимум квадратного трехчлена от  (найти вершину параболы):
(найти вершину параболы): 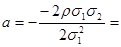
 . Подставляя это значение, найдем
. Подставляя это значение, найдем
 . Вычислим погрешность оценки при этих значениях параметров
. Вычислим погрешность оценки при этих значениях параметров
 .
.
При линейной зависимости  оценка точна, погрешность равна нулю.
оценка точна, погрешность равна нулю.
Чем меньше коэффициент корреляции, тем грубее оценка. В крайнем случае, при отсутствии корреляции ( )
)  .
.


















