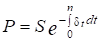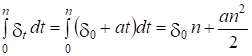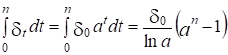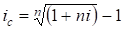Начисление сложных процентов
ГЛАВА 2. Начисление сложных процентов
Начисление простых процентов применяется в практике в краткосрочных периодах. В долгосрочных финансовых операциях проценты не выплачиваются после их начисления, а присоединяются к основной сумме, т.е. происходит их капитализация. База для начисления процентов в каждом последующем периоде регулярно изменяется. В этом случае говорят об использовании сложных процентов.
Если в процессе реинвестирования предположить, что ставка процентов и интервалы времени одинаковы, то мы получим формулу сложных процентов (рис. 3):
| S = P(1 + i)n, | (9) |
где i - ставка сложного процента,
(1 + i)n - множитель наращения по сложным процентам.
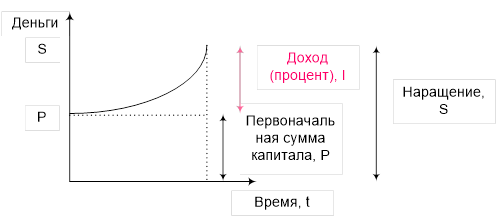
Рисунок 3 – Наращение сложных процентов
Необходимо отметить, что сила роста по сложным процентам приводит порой к впечатляющим результатам.
Рекомендуемые материалы
Остров Манхэттен был «куплен» в 1624 году у индейского вождя за $24. Через 350 лет (1974 год) стоимость земли оценивалась в $40 млрд. Ставка сложных годовых процентов составила 6.25 %.
2.1. Дискретное начисление сложных процентов несколько раз в году
Проценты, как правило, капитализируются не один, а несколько раз в году. Изначально же оговаривается годовая ставка j с указанием периода начисления m. В этом случае наращение S будет определяться как
| S = P(1 + j/m)mn, | (10) |
где j - номинальная годовая ставка процента;
m - число периодов начисления в году;
j / m - ставка в течение периода;
mn - число начислений процентов весь срок операции.
В зависимости от частоты начисления процентов наращение суммы происходит различными темпами, причем с возрастанием частоты накопленная сумма увеличивается.
Ставки процента могут изменяться во времени (плавающие ставки).
| S = P(1 + i1)n1(1 + i2)n2(…) |
Часто срок начисления не является целым числом. В правилах банков для некоторых операций в этих случаях существуют два метода:
1) общий метод - расчет ведется по формулам сложных процентов.
2) смешанный метод - за целое число лет начисляются сложные проценты, за дробную часть - простые.
| S = P(1+i)a (1+bi), |
где a + b = n – период операции,
a – целое число лет,
b – дробная часть года.
Если дата начала операции и дата окончания операции лежат в смежных периодах, то начисленные проценты не могут быть целиком отнесены к одному из периодов. Это характерно для ситуаций, возникающих в бухгалтерском учете, налогообложении, финансовом анализе.
В случае простых процентов имеем
| I = I1 + I2 = Pn1i + Pn2i |
При условии начисления сложных процентов
| I = I1 + I2 I1 = P [(1 + i)n1 - 1], I2 = P (1 + i)n1[(1 + i)n2 - 1] |
2.2. Непрерывное начисление сложных процентов
Максимально возможное наращение осуществляется при бесконечном дроблении годового интервала, т.е. при m ® ¥. Это имеет большее значение в количественном финансово-экономическом анализе сложных производственных и хозяйственных объектов и явлений, например при обосновании и выборе инвестиционных решений.
Необходимость применения непрерывного наращения (или непрерывных процессов) определяются тем, что многие экономические явления по своей природе непрерывны, поэтому их аналитическое описание с помощью непрерывных процентов более адекватно.
При непрерывном наращении используется особый вид процентной ставки - сила роста (d). Сила роста характеризует относительный прирост наращенной суммы в бесконечно малом промежутке времени (номинальная ставка при m ® ¥). Сила роста может быть постоянной или изменяться во времени.
Так как из курса математического анализа известно, что  , то
, то  .
.
Таким образом,
| S = Pend, | (11) |
где d - сила роста.
Возможно использование переменной силы роста, когда d изменяется, следуя определенному закону, т.е. dt = f (t) - функция, тогда
|
|
Наиболее часто встречаются в аналитических расчетах линейные и экспоненциальные функции.
В случае линейного изменения силы роста
| dt = d0 + at, |
где d0 - начальное значение силы роста,
a - абсолютный прирост.
|
|
В случае экспоненциального изменения силы роста
| dt = d0at, |
где d0 - начальное значение силы роста,
a - постоянный темп роста
|
|
2.3. Дисконтирование по сложным процентам
По сложным процентам проводится и дисконтирование. Математическое дисконтирование основывается на использовании формул (9), (10), (11)
| P = S (1 + j/m)-mn P = Se-dn. |
Банковский учет предполагает использование сложной учетной ставки.
| P = S(1 - dc)n, | (12) |
где dc - сложная учетная ставка.
Если дисконтирование проводится m раз в году, то предполагается использование номинальной учетной ставки f:
| P = S(1 - f/m)mn | (13) |
где f - номинальная годовая учетная ставка;
m - число периодов дисконтирования в году;
f / m - учетная ставка в течение периода;
mn - число процедур дисконтирования за весь срок операции.
2.4. Принцип финансовой эквивалентности
Процентные и учетные ставки решают один и те же задачи: определяют степень доходности при операциях наращения или размеры дисконтированных сумм при учетных операциях. В связи с этим возможен выбор таких процентных или учетных ставок, при использовании которых финансовые последствия окажутся равноценными.
Можно утверждать, что принцип финансовой эквивалентности соблюдается, если при изменении любых параметров операции финансовый результат не изменяется. Применение принципа финансовой эквивалентности позволяет решать целый класс аналитических задач.
Эквивалентные ставки - ставки, использование которых приводит к одинаковым финансовым результатам. Эквивалентная ставка, которая будет давать тот же результат, что и оговоренная изначально величина, - эффективная ставка.
Решения задачи и нахождение эквивалентных ставок основывается на равенстве финансовых результатов на выбранный момент времени (на начало или конец операции) по вариантам. Ниже приводятся некоторые соотношения эквивалентности, которые представляют собой наибольшее практическое значение.
Эквивалентность сложных процентных ставок может быть описана на основании формул (9) и (10) следующим образом
| (1 + iэ)n = (1 + j/m)mn, откуда iэ = (1 + j/m)m -1 |
Эквивалентность сложных учетных ставок может быть определена на основании (12) и (13)
| (1 - f / m)mn = (1 – dэ)n, откуда dэ = 1 - (1 - f / m)m |
Эквивалентность простых процентных и учетных ставок выводится исходя из (5) и (8):
| (1 + ni) = (1 - nd)-1, откуда i = d / (1 - nd) или d = i /(1 + ni) |
Эквивалентность простых и сложных процентных ставок определяется с использованием формул (5) и (9):
| (1 + ni) = (1 + ic)n, откуда i = ((1 + ic)n - 1) / n
|
Определение эквивалентности сложных дискретных и непрерывных процентов основано на формулах (10) и (11):
| (1 + j/m)m = ed, откуда Люди также интересуются этой лекцией: Современная Россия. j = (ed/m - 1)m или d= m ln(1 + j/m) |
Эквивалентность сложных учетных ставок и ставок непрерывных процентов:
| dc = 1 - e-d d = - ln (1 - dc) |
Таким образом, решение задачи сводится к сравнению либо множителей наращения, либо дисконтных множителей.



 и
и