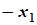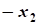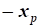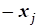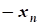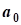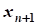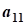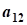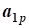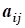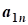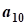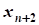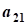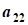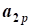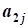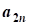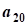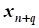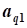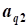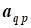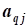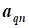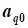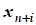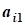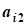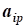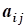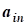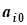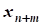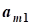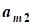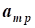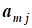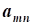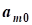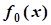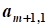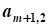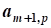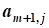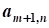Линейное программирование
Линейное программирование
Постановка задачи линейного программирования.
Найти 
f0(x)=c1x1+c2x2+...+cnxn (1)
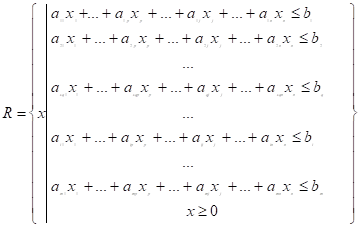
где x=(x1,x2,...,xn)-вектор переменной
cj, j=1,2,...,n- коэффициенты целевой функции
Рекомендуемые материалы
aij, i=1,2,...,n; j=1,2,...,n- коэффициент ограничений
b=(b1,b2,...,bn)-вектор свободных членов
A=[aij]m´n
ЗЛП в стандартной форме записи:
[f0(x)=
] 
[g0(y)=
]
R=
Q=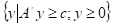
Где: АТ-транспонированная матрица AТ=[aij]m´n
ЗЛП в канонической форме записи:
[f0(x)=] [g0(y)=]
R=
Q=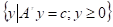
Эквивалентные преобразования ЗЛП.
Эквивалентные преобразования не изменяют решения ЗЛП , то есть эквивалентность относительно решения.
1. Переход от задачи max к задаче min:
[f0(x)=]-от этой задачи перейти к задаче на min
f0(x)= -[f0(x)]
f0(x)==[-]
g0(y)== -
g0(y)=[]
2.Переход от ограничения равенства к ограничению неравенства (заключается в переходе к двум противоположным неравенствам).
³bi
£bi
При решении задачи на f0(x) имеем следующие ограничения:
-£bi
£bi
При решении задачи на f0(x) ограничения следующие:
³bi
-³bi
3. Переход от ограничений неравенств к ограничениям равенства:
£bi добавляется неотрицателбная часть: +xn+i=bi, где xn+i³0 (дополнительная переменная)
³cj вычтем константу : -xm+j=cj ,где xм+j³0
4. Переход от переменной неопределённого знака к неотрицательной переменной.
x ³£ 0
Введём две новые переменные:Uj³ 0;
Vj³0.
Получим: xj= Uj -Vj
5. Переход от переменной, ограниченной сверху к неотрицательной переменной:
xk³dk, dk=const,dk>0
Введём новые переменные: Wk=xk-dk , Wk>0
Замечание: не допускается деление ограничений на какое-либо число или умножение ,так как при этом изменяется решение ЗЛП, то есть получаем задачу . не эквивалентную исходной.
Симплекс – метод решения задачи линейного программирования на максимум в стандартной форме записи при 
.
Симплекс – метод для решения задачи линейного программирования на максимум основан на методе Жордана (1838-1922) решения систем линейных алгебраических уравнений.
Американский математик Дж. Данциг в 1949 году введением строки для целевой функции применил этот метод для решения задачи линейного программирования.
Основоположником же рассматриваемого метода считается Канторович, представивший в 1938 году “метод допустимого улучшения плана”, предполагая, что начальное решение уже имеется, в отличие от Данцига, у которого начальное решение находится с помощью симплекс – преобразований. Однако Нобелевская премия была получена им лишь в 1975 году.
Отличие данного метода от других в том, что в симплекс – таблицу записываются только уравнения, т. е. из стандартной формы записи надо перейти к канонической. Для решения задач в стандартной форме используются модифицированные жордановы исключения.
Рассмотрим симплекс – метод решения задачи линейного программирования на максимум в стандартной форме записи на следующем примере:
.
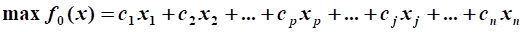
От задачи (1) – (3) перейдем к задаче в канонической форме записи. Для этого введем дополнительные переменные 
и разрешим относительно них систему ограничений – равенств, при этом 
:
.
Введем вектор 
, т. е.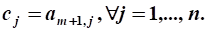 
Тогда
Заметим, что симплекс – метод применяется только при выполнении ограничения (3).
Введем множество базисных переменных 
и множество небазисных переменных 
и применим приведенный ниже алгоритм решения задачи линейного программирования на максимум к рассматриваемой задаче:
1. 
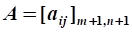
2. 
- начало итерационного процесса
3. 
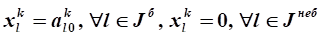
4. 
иначе см. пункт 12 (столбец 
будет разрешающим)
5. 
иначе см. пункт 14
6. 
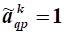
7. 
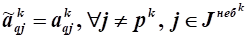
8. 
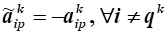
9. 
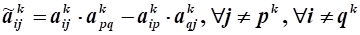
10. 
- переход к следующей итерации.
11. 
- новый базис. Далее переходим на пункт 3.
Особенности алгоритма.
12. Если 
, то существует альтернативный оптимум, и см. пункт 5
13. 
, то найдено оптимальное решение, иначе см. пункт 14.
14. Задача линейного программирования не имеет смысла.
15. Конец
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| Рекомендуем посмотреть лекцию "25 Ветеринарно-санитарная оценка молока. Способы и режимы обеззараживания молока".
|
|
|
|
|
|
