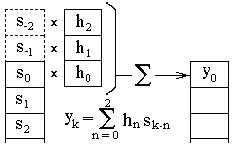Динамическое представление сигналов

Тема 3:  динамическое  представление  сигналов

Вовсе не безразлично, каким образом следует разрезать курицу или зайца.

Децим Юний Ювенал. Сатиры.

Римский поэт-сатирик (I-II в.).

Римлянин с высшим образованием не мог себе позволить без соответствующего философского обоснования потрошить курицу, а тем более зайца. Но лично меня всегда больше интересует, что я с этого буду иметь.

Владимир Бакаев. Комментарии.

Уральский геофизик (XX-XXI в.).

Содержание:  3.1. Разложение сигналов по единичным импульсам. Единичные импульсы. Разложение сигнала. Импульсный отклик линейной системы. 3.2. Свертка (конволюция). Интеграл Дюамеля. Техника свертки. Свойства свертки. Системы свертки. Начальные условия свертки. Литература.

3.1.  Разложение сигналов по единичным импульсам [1,11].

Рекомендуемые материалы

Динамическая форма представления сигналов соответствует их естественной и привычной для нас форме математического описания в виде функций независимых переменных (аргументов). Моделирование и анализ линейных стационарных систем обработки сигналов произвольной формы в динамическом представлении базируется на разложении сигналов по единичным импульсам простейшей формы.

Единичные импульсы. В качестве математической модели единичного импульса при анализе аналоговых сигналов используют дельта-функцию.

Дельта-функция описывается следующими математическими выражениями:

d(t-t) = 0   при t ¹ t,       d(t-t) dt = 1.

Функция d(t-t) равна нулю везде за исключением точки t, в которой она бесконечно велика и не является дифференцируемой. На практике такие функции не могут быть реализованы с абсолютной точностью. Но во всех случаях, когда площадь импульса равна 1, а реакция системы на импульс во много раз больше длительности самого импульса, входной сигнал можно считать единичной импульсной функцией со свойствами дельта - функции.

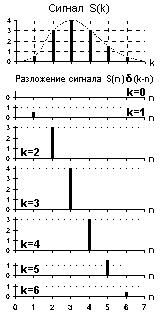
Функция Кронекера. Для дискретных и цифровых систем в качестве единичного импульса используется дискретный интегральный аналог дельта-функции - функция единичного отсчета d(kDt-nDt), которая равна 1 в координатной точке k = n и нулю во всех остальных точках, при этом функция d(kDt-nDt) определена только для целых значений координат k и n.

Математические выражения d(t-t) и d(kDt-nDt) называют также импульсами Дирака и Кронекера. Однако, применяя такую терминологию, не следует забывать, что это не просто единичные импульсы в координатных точках t и nDt, а импульсные функции, определяющие как значения импульсов в определенных координатных точках, так и нулевые значения по всем остальным координатам, в пределе от -¥ до  ¥. 

Разложение сигнала. Импульсы Дирака и Кронекера используются для разложения, соответственно, произвольных аналоговых сигналов s(t) и дискретных сигналов s(kDt) в непрерывную последовательность неперекрывающихся  (ортогональных) импульсов:

s(t) =s(t)d(t-t) dt.                                                    (3.1.1)

     s(kDt) =s(nDt)d(kDt-nDt).                                  (3.1.1')

Для аналоговых сигналов разложение (3.1.1) в физическом представлении эквивалентно сканированию значений сигнала s(t) в моменты времени t = t бесконечно узкой щелью, бегущей вдоль оси t. Для цифровых сигналов эта щель равна одному отсчету. Пример разложения дискретного сигнала приведен на рис. 3.1.1.

Единичные импульсные функции d(t-t), -¥<t< ¥, и d(kDt-nDt), -¥<n<¥, образуют в бесконечномерных пространствах системы координатных базисов {d(t-t)} и {d(kDt-nDt)}, т.к. единичные импульсные функции не перекрываются и, соответственно, взаимно ортогональны. По этим координатным системам и производится разложение сигналов  s(t) и s(kDt). Совокупности проекций сигналов на координатные базисы представляют собой векторные описания сигналов.

Импульсный отклик линейной системы. Если на вход линейной системы в момент времени t = 0 подать единичный импульс (Дирака или Кронекера, в зависимости от типа системы), то на выходе мы получим реакцию системы на единичный входной сигнал. Эта реакция называется функцией импульсного отклика системы или импульсной характеристикой. Она однозначно определяется оператором преобразования h(..):

y(t) = T[d(t-0)] = h(t).                                              (3.1.2)

     y(kDt) = T[d(kDt-0)] = h(kDt).                                       (3.1.2')

Импульсный отклик аналоговой системы на входную дельта-функцию также в определенной степени представляет собой математическую абстракцию идеального преобразования. С практической точки зрения под импульсным откликом можно понимать отображение реакции системы на импульсный входной сигнал произвольной формы с единичной площадью, если длительность этого сигнала пренебрежимо мала по сравнению с временной (координатной) разрешающей способностью системы. Для цифровых систем импульсный отклик однозначно определяется реакцией системы на импульс Кронекера. Функцию импульсного отклика называют также весовой функцией системы.

Очевидно, что в линейных и инвариантных к сдвигу системах форма импульсного отклика не зависит от времени прихода входного сигнала и определяет только его положение на временной оси. Так, если входной импульс задержан (относительно 0) на время t_o, то соответствующий выходной сигнал будет определяться выражением:

y(t) = T[d(t-t_o)] = h(t-t_o).

            В любой системе, работающей в реальном масштабе времени, сигнала на выходе системы не может быть, если нет сигнала на ее входе. Отсюда следует односторонность импульсного отклика физических систем:

h(t-t) = 0   при   t<t.

            Для программных систем, работающих с зарегистрированными массивами цифровых данных, импульсный отклик может быть и двусторонним, так как при обработке сигналов в любой текущей точке kDt системе доступны как "прошлые" отсчеты kDt-nDt, так и "будущие" отсчеты kDt+nDt. Это резко расширяет возможности программной обработки сигналов по сравнению с физическими системами.

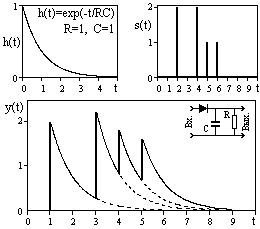
На рисунке 3.1.2 приведен пример импульсного отклика h(t) элементарной физической системы преобразования электрических сигналов – динамической интегрирующей RC-цепи. Подобные схемы очень часто применяются в полевых геофизических приборах (например, в радиометрах) в качестве интенсиметров - измерителей средней скорости счета импульсных потоков сигналов.

При подаче на вход RC-цепи единичного и очень короткого (Dt << RC) импульса заряда Dq емкость С заряжается до напряжения V_о = Dq/C и начинает разряжаться через сопротивление R, при этом напряжение на емкости изменяется по закону v(t) = V_oexp(-t/RC) = (Dq/C)exp(-t/RC). Отсюда, импульсный отклик RC-цепи на единичный входной сигнал с единичным значением заряда Dq = 1 равен:  h(t) = (1/C)exp(-t/RC), где форма отклика определяется функцией экспоненты, а множитель (1/С) является масштабным преобразователем сигнала (заряда в напряжение). По существу, импульсным откликом системы определяется доля входного сигнала, которая действует на выходе системы по истечении времени t после поступления сигнала на вход (запаздывающая реакция системы).

Если функция импульсного отклика системы известна, то, с учетом принципа суперпозиции сигналов в линейной системе, можно выполнить расчет реакции системы в любой произвольный момент времени на любое количество входных сигналов в любые моменты времени их прихода путем суммирования запаздывающих реакций системы на эти входные сигналы. На рис. 3.1.2 приведен пример входного сигнала s(t) для RC-цепи в виде последовательности импульсов и  реакция системы y(t) на такой входной сигнал, образованная суммированием реакций системы на каждый импульс.

Допустим, что на вход RC-цепи в моменты времени t₁=1 и t₂=2 поступили очень короткие (по сравнению со значением RC) импульсы заряда величиной A и В. Математически это можно отобразить сигналом s(t) = q₁(t)+q₂(t), где q₁(t) = A×d(t-t₁) и q₂ = B×d(t-t₂). Выходной сигнал системы при известном импульсном отклике h(t) отобразится формулой:

y(t) = T[q₁(t)+q₂(t)] = T[Ad(t-t₁)]+T[Bd(t-t₂)] = A×T[d(t-t₁)]+B×T[d(t-t₂)] = A×h(t-t₁)+B×h(t-t₂).

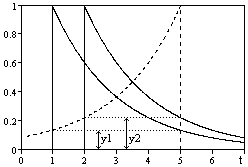
            При расчете значений выходного сигнала в произвольный момент времени t после прихода на вход системы сигналов q₁ и q₂, например, для t = 5, для каждого из сигналов вычисляются значения их запаздывающих реакций: y1 = A×h(5-1) = A×h(4) и y2 = B×h(5-2) = B×h(3), после чего значения запаздывающих реакций суммируются у = у1+у2. Пример этой операции можно видеть на рис. 3.1.3, где для удобства графического представления приняты значения А=1 и В=1. Сущность операции не изменяется при любых значениях А и В, а в общем случае и для любого количества импульсов.

            Однако эту же операцию можно рассматривать и с другой позиции. Развернем импульсный отклик h(t) системы на 180⁰ и поместим его начало h(0) непосредственно в точку, для которой нужно выполнить расчет выходного сигнала, т.е. в точку t=5 для нашего примера. Если теперь отсчет координат для функции h(t) повести назад от точки расчета по аргументу t, т.е. перейти на вычисление h(t), где значение t изменяется от 0 и далее (в пределе до  ¥), то нетрудно убедиться (на рисунке это наглядно видно), что функция h(t) пересечет входные импульсы на тех же значениях у1 и у2. Для этих точек пересечения первого и второго импульсов соответственно имеет место t₁ = t-t₁ и t₂ = t-t₂, как и при прямом методе расчета запаздывающих реакций при расчете значений h(t-t₁) и h(t-t₂). После умножения полученных значений h(t₁) и h(t₂) на значения входного сигнала А и В получаем полную аналогию: y1 = A×h(t₁) = A×h(t-t₁) и y2 = B×h(t₂) = B×h(t-t₂), и соответственно суммарный сигнал у = у1+у2.

            Такое, чисто математическое представление расчета более удобно для составления математических алгоритмов вычислений. Условно этот процесс для коротких входных импульсных сигналов может быть представлен в следующем виде. Для любой точки расчета t_i выходного сигнала инвертированная по направлению функция импульсного отклика h(t) помещается в эту точку t_i и просматривается по своей координате t с одновременным синхронным просмотром входного сигнала s(t) назад от точки расчета (прошлые значения входного сигнала), т.е. по координатам t_i-t. Значения всех встреченных при просмотре импульсов s(t_i-t) перемножаются со значениями h(t) и суммируются, т.е. для каждой текущей точки расчета t_i в аналоговой системе выполняется операция:

y(t_i) =h(t)×s(t_i-t) dt.                                            (3.1.3)

            Соответственно в цифровых системах для произвольной точки k_i:

    y(k_iDt) =h(nDt)×s(k_iDt-nDt).                                     (3.1.3')

Полученная сумма значений и будет представлять собой запаздывающую реакцию системы на все импульсы, поступившие на вход системы до текущей точки расчета выходного сигнала.

Таким образом, для линейных и стационарных систем легко определить их реакцию на любой входной сигнал, если известен импульсный отклик систем на единичный входной сигнал.

3.2.  Свертка (конволюция) [1,11].

Интеграл Дюамеля. Произвольный сигнал на входе системы с использованием выражений разложения сигнала может быть представлен в виде последовательной линейной комбинации взвешенных единичных импульсов:

y(t) = T[s(t)] = T[s(t)d(t-t) dt].

            На основании принципа суперпозиции линейный оператор Т может быть внесен под знак интеграла, т.к. последний представляет собой предельное значение суммы. При этом операция преобразования действует только по переменной t. Отсюда следует:

y(t) = s(t) Т[d(t-t)] dt = s(t) h(t-t) dt.                      (3.2.1)

            Это выражение представляет собой интеграл Дюамеля или свертку (конволюцию) входного сигнала с импульсной характеристикой системы. Заменой переменных t-t = t можно убедиться в том, что свертка коммутативна:

    s(t) h(t-t) dt ºh(t) s(t-t) dt.                                 (3.2.1')

Аналогично, для дискретных сигналов:

       y(kDt) =h(nDt) s(kDt-nDt).                                  (3.2.1'')

Выражения (3.2.1) имеют специальную форму упрощенной математической записи в символическом виде:

y(t) = s(t-t) _* h(t) º s(t) _* h(t).

Сравнением выражений (3.2.1' и 3.2.1'') с выражениями (3.1.3) нетрудно убедиться в их полной идентичности, за исключением нижнего предела интегрирования (суммирования). Это и понятно, так как выражения (3.1.3) были получены при рассмотрении реальной физической системы, работающей в реальном масштабе времени, импульсный отклик которых является односторонним (равен нулю при t<0). Для таких систем интегрирование (и суммирование) от -¥ до 0 не имеет смысла. Кроме того, в реальных физических системах импульсный отклик, как правило, отличен от нуля только на определенном интервале, при этом верхний интервал интегрирования (суммирования) в выражениях (3.2.1) также может устанавливаться равным значению этого интервала. В общем случае пределы интегрирования (суммирования) ограничиваются значениями t, на которых функция h(t) существует или имеет значимые значения.

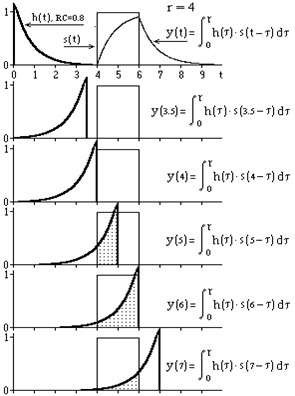
Техника свертки. Для вычисления свертки по выражению (3.2.1') функция импульсного отклика реверсируется по своей координате, т.е. строится в режиме обратного времени, и движется относительно функции входного сигнала в сторону возрастания значений t. В каждый текущий момент времени значения обеих функций перемножаются (по всем значениям своих аргументов), а произведение интегрируется. Полученный результат относится к той координатной точке, против которой находится значение импульсного отклика h(0).

На рис. 3.2.1. приведен пример выполнения свертки прямоугольного импульса  с импульсным откликом RC-цепи, площадь которого нормирована к 1. Если площадь импульсного отклика h(t) равна 1, то площадь выходного сигнала свертки всегда должна быть равна площади входного сигнала, что можно видеть на верхнем графике рисунка, при этом одномасштабное сравнение  входного и выходного сигналов наглядно демонстрирует характер преобразования сигнала в данной системе. На последующих графиках рисунка демонстрируется вычисление результатов свертки в ряде последовательных точек t_i = {3.5, 4, 5, 6, 7} временной оси. В силу отрицательного знака t в аргументах функции s(t-t) интегрирование произведения h(t)s(t-t) выполняется назад по времени и может ограничиваться только определенной длиной значимых значений импульсного отклика (которая в данном случае установлена равной r = 4), а результат относится к начальной точке h(0) импульсного отклика. Так как входной сигнал, рассмотренный на рисунке, представляет собой прямоугольный импульс с амплитудой 1, то интеграл свертки в каждой текущей точке расчета равен площади импульсного отклика в пределах границ входного прямоугольного импульса (заполнено точками).

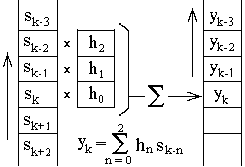
Еще более наглядна техника выполнения цифровой свертки, приведенная на рис. 3.2.2. Для вычисления свертки массив одной из функций (s_k - входного или свертываемого сигнала) располагается по ходу возрастания номеров. Массив второй функции (h_n - более короткой, которая обычно называется оператором свертки или оператором фильтра), строится параллельно первому массиву в обратном порядке (по ходу уменьшения номеров первого массива или в режиме обратного времени). Для вычисления y_k значение h₀ располагается против s_k, все значения s_k-n  перемножаются с расположенными против них значениями h_n и суммируются. Результаты суммирования являются выходным значением функции y_k, после чего оператор h_n сдвигается на один номер k вперед (или функция s_k сдвигается ему навстречу) и вычисление повторяется для номера k+1 и т.д.

Свойства свертки. Для свертки характерны следующие свойства:

1. Дистрибутивность:

h(t) _* [a(t)+b(t)] = h(t) _* a(t)+h(t) _* b(t).

2. Коммутативность:

h(t) _* a(t) _* b(t) = a(t) _* b(t) _* h(t).

3. Ассоциативность:

[a(t) _* b(t)] _* h(t) = h(t) _* a(t) _* b(t).

Преобразование свертки однозначно определяет выходной сигнал y(t) для установленного значения входного сигнала s(t) при известном значении функции импульсного отклика системы h(t). Обратная задача деконволюции - определение функции s(t) по функциям y(t) и h(t), относится к разряду некорректных и имеет решение только при вполне определенных условиях. Это объясняется тем, что свертка может существенно изменить частотный спектр сигнала y(t) относительно s(t) и восстановление функции s(t) становится невозможным, если определенные частоты ее спектра в сигнале y(t) полностью утрачены.

Любая практическая система должна быть устойчивой, т.е. для сигналов, конечных по энергии или средней мощности, выходные сигналы также должны быть конечными по этим параметрам. Устойчивость обеспечивается при выполнении условия абсолютной интегрируемости импульсного отклика системы:

|h(t)| dt < ¥.

Для систем с m входами и n выходами аналогично определяются парциальные импульсные отклики h_ij(t),  i = {1,2, ... ,n},  j = {1,2, ... ,m}, каждым из которых отображается сигнал на i-м выходе при поступлении сигнала d(t) на j-й вход. Полная совокупность импульсных откликов образует матрицу:

,

а выражение свертки приобретает вид:

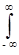
(t) = (t)(t-t) dt.

            Здесь (и в дальнейшем тексте) жирным шрифтом выделяются векторные величины.

Системы свертки. Свертка выполняется системой (физическим или программным устройством). Физические системы, работающие в реальном времени, вычисляют текущее значение выходного сигнала по всем прошлым значениям входного сигнала и не могут иметь в своем распоряжении будущих значений входного сигнала. Операторы таких систем являются односторонними (каузальными). Вышеприведенная нормированная к 1 по площади функция RC-цепи h(t) = (1/RC)×exp(-t/RC), принятая в качестве системного оператора на рис. 3.2.1, является именно таким односторонним каузальным оператором. При сравнении выходного сигнала такой системы с входным нетрудно заметить, что выходной сигнал сдвигается относительно входного сигнала. Для каузальных систем такой "сдвиг по фазе" существует всегда и не может быть исключен (сигнал на выходе системы не может быть раньше сигнала на ее входе).

            Входным сигналом программных систем является сигнал в целом, записанный в память вычислительного устройства. При обработке таких данных в распоряжении системы при вычислении любой текущей точки выходного сигнала имеются как "прошлые" для данной точки, так и "будущие" значения входного сигнала. Это позволяет создавать системы без сдвига фазы выходного сигнала относительно входного. Для создания таких систем может использоваться два способа:

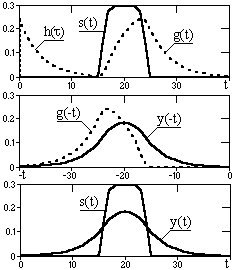
            1. Первый способ иллюстрирует рис. 3.2.3. Задается система с односторонним каузальным оператором h(t). Входной сигнал s(t) пропускается через систему в обычном порядке и выполняется свертка g(t) = h(t)_*s(t). Затем выходной сигнал g(t) реверсируется (g(t)=>g(-t), конец сигнала становится его началом в порядке возрастания t) и повторно пропускается через систему, т.е. выполняется свертка y(-t) = h(t)_*g(-t) . Полученный сигнал снова реверсируется (y(-t) => y(t) = h(-t)_*g(t)) и является окончательным выходным сигналом y(t) системы. Три последние операции (реверс g(t) Þ свертка c h(t) Þ реверс выходного сигнала) эквивалентны свертке сигнала g(t) с реверсированным откликом системы h(-t), и сдвиг по фазе при свертке реверсированного сигнала компенсирует сдвиг по фазе сигнала, полученный при первой свертке. Общий результат операции  y(t) = h(t)_*h(-t)_*s(t) не имеет сдвига по фазе выходного сигнала относительно входного. Такую операцию приходится выполнять для исключения сдвига фазы при применении рекурсивных фильтров, которые всегда являются односторонними.

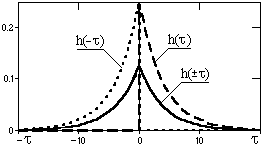
            2. Выходной результат y(t) = h(t)_*h(-t)_*s(t) предыдущей операции позволяет, используя свойство коммутативности свертки, сначала выполнить свертку h(t)_*h(-t) = h(±t) и получить один системный оператор h(±t) (см. рис. 3.2.4), обеспечивающий свертку без сдвига фазы. Этот системный оператор является двусторонним и симметричным относительно t = 0. Но использование его возможно только для предварительно записанных сигналов, т.к. при выполнении свертки y(t)= h(±t)_*s(t-t) для отрицательных значений t требуются "будущие" значения входного сигнала s(t+t). Результат свертки с симметричным оператором полностью аналогичен первой операции (сигнал y(t) на рис. 3.2.3).

            Приведенное выше формирование двустороннего симметричного оператора свертки имеет чисто познавательный характер. На практике вполне естественным является расчет непосредственно симметричных двусторонних операторов под требуемые задачи обработки числовых данных (сигналов, зарегистрированных в дискретной числовой форме).

Начальные условия свертки. В начальный момент свертки, при вычислении значений y(t_i) для значений t_i < t_max оператора h(t), функция оператора, построенная в режиме обратного времени, при t>t_i "зависает" для значений t_i-t против отсутствующих значений входной функции. Пример такого зависания оператора дискретной свертки  против несуществующих отсчетов  s_-1 и s_-2 входного массива данных при вычислении отсчета у₀ приведен на рис. 3.2.5. Зависание исключают либо заданием начальных условий - дополнительных отсчетов, чаще всего нулевых или равных первому отсчету входной функции, либо началом свертки с отсчета входной функции k_i = n_max с соответствующим сокращением интервала выходной функции на интервал задания системного оператора. Для симметричных операторов со значениями -n (вперед по времени) такой же момент наступает и в конце входного массива и требует задания конечных условий или сокращения размера выходного сигнала.